Frequenz- und Zeitmessung#
Häufig liegen uns frequenzmodulierte Spannungssignale vor. Die Frequenz ist hierbei der Informationsträger und muss ausgelesen werden, um die Messgröße \(x\) zu bestimmen. Mitunter benutzt man hierfür eine Zeitmessung, um die Periodendauer zu bestimmen. Der Vorteil, eine Messgröße an die Frequenz eines Signals zu übergeben, ist die Stabilität der Frequenz und damit geringe Messabweichung und hohe Genauigkeit, mit der wir Frequenzen bzw. Zeiten messen können, da uns hier präzise Frequenz- bzw. Zeitnormale in Form von Quarzgeneratoren oder sogar Atomuhren zur Verfügung stehen. Diese Normale liefern eine um den Faktor \(10^7\)-\(10^8\) bessere Genaugkeit als Referenznormale anderer physikalischer Größen, wie z.B. der Spannung.
Frequenzmessung#
Das Grundprinzip der Frequenzmessung ist in F_messung dargestellt. Die Grundidee basiert darauf zu zählen, wie viele Perioden innerhalb einer bestimmten Zeit auftreten.
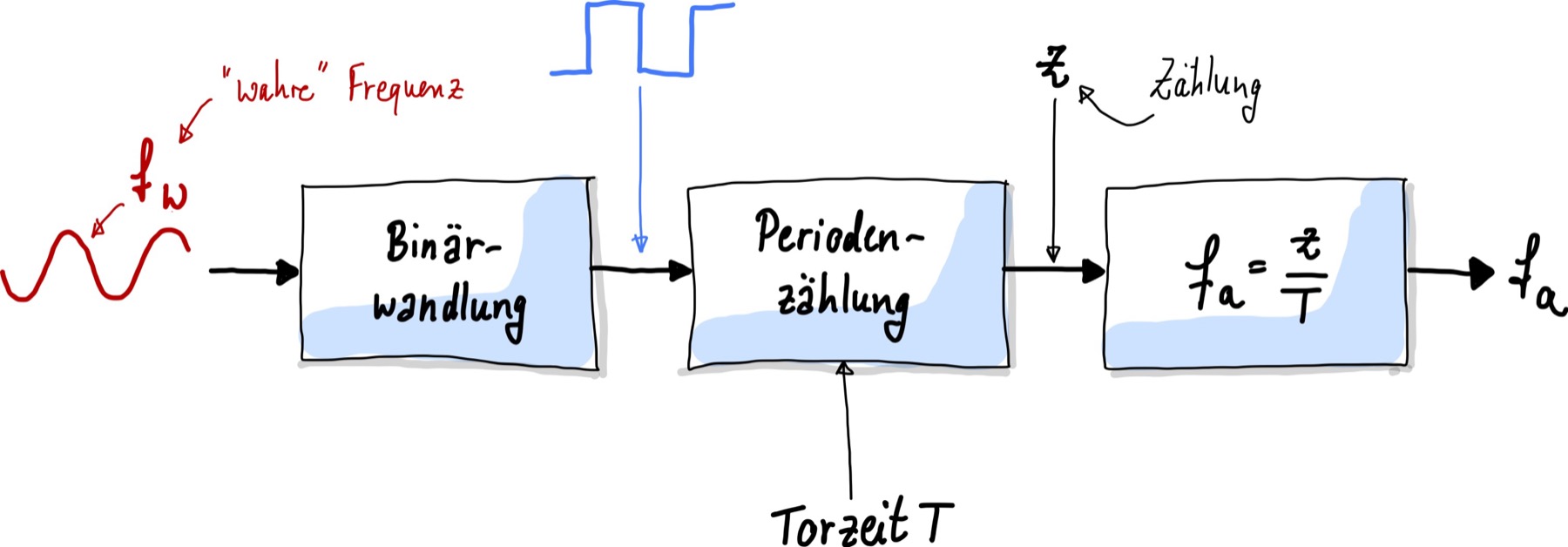
Grundprinzip der Frequenzmessung.#
In der ersten Stufe wird das periodische Eingangssignal in eine binäres Signal mit der gleichen Frequenz umgewandelt. Hierfür werden üblicherweise Operationsverstärker benutzt
Dann zählt man über eine bestimmte Zeit, die Torzeit \(T\) die Anzahl \(z\) der Perioden. Das Bauteil Tor ist eine digitale Grundschaltung und besteht aus einer UND-Verknüpfung. Diese kombinatorische Schaltung liefert nur dann einen logischen 1-Pegel am Ausgang, wenn alle Eingänge mit einem logischen 1-Pegel beaufschlaft sind. An einem Eingang wird die präzise Messzeit eingestellt. Solange diese angelegt ist, wird am zweiten Messeingang die Anzahl von digitalen Pulsen gezählt.
Der Messwert ergibt sich aus dem Verhältnis von gezählten Perioden und der Torzeit:
Hierbei können Zählfehler passieren, da die Torzeit \(T\) unabhängig von der Periodendauer und dem Messsignal ist. D.h. im schlimmsten Fall kann man sich um eine ganze Periode verzählen, weshalb die Messabweichung der Zählung \(\Delta z = 1\) ist. Dieses Phänomen ist in F_zählung dargestellt.
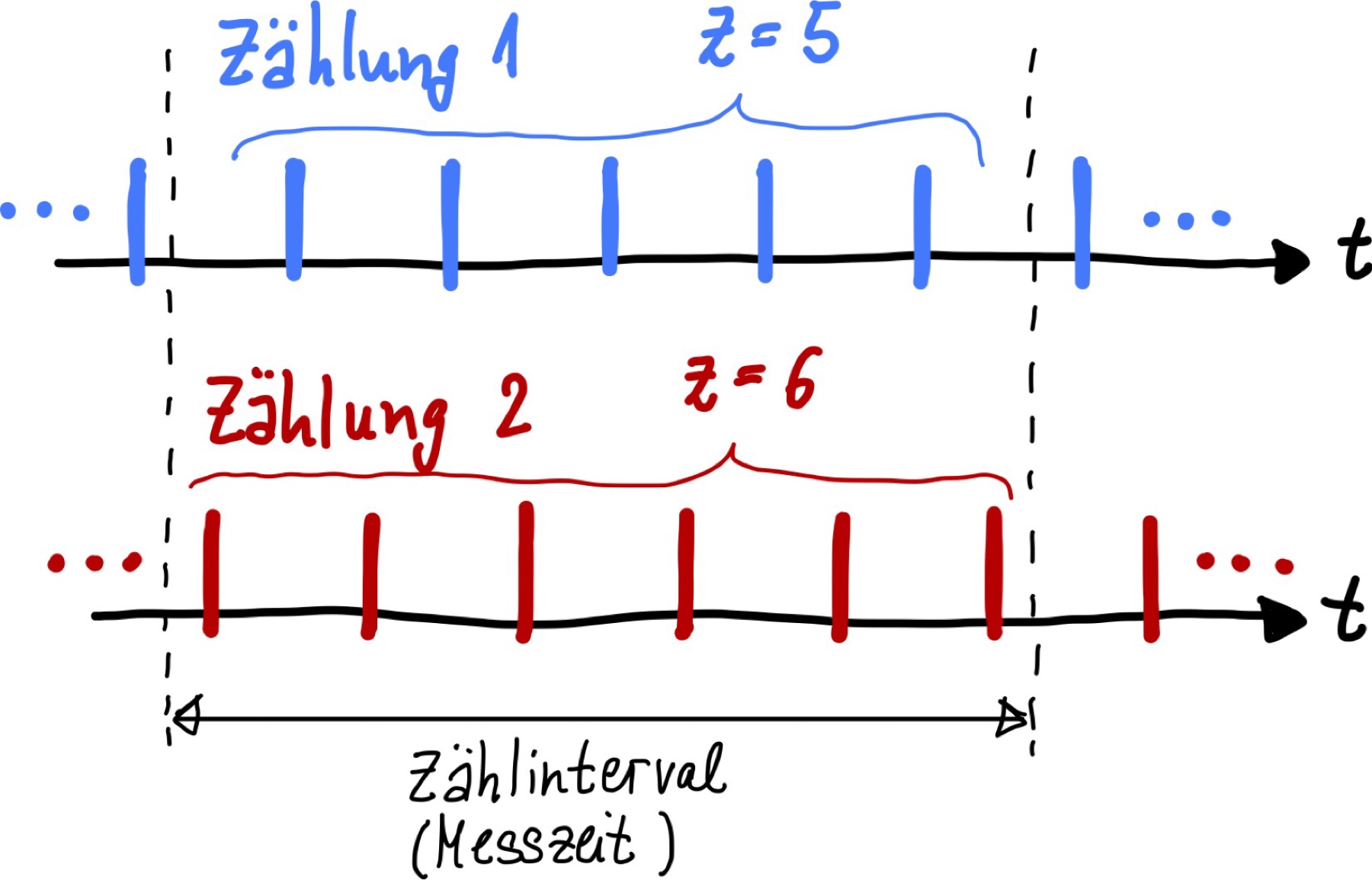
Zählfehler#
Die maximal zu erwartende Quantisierungsabweichung bezogen auf der Frequenzmessung beträgt also
Wenn wir also die Frequenz eines \(100\,\mathrm{Hz}\)-Signals über eine Torzeit von \(1\,\mathrm{s}\) bestimmen (was schon eine verdammt lange Messzeit ist) erhalten wir eine Maximalabweichung von \(1\,\mathrm{Hz}\), also 1% bezogen auf den Messwert. Je niederiger die Frequenz, desto länger müssen wir messen, um ein genaues Ergebnise zu erhalten.
Show code cell source
T = 1000e-3
print('Die maximale Messabweichung beträgt:' ,1/T, 'Hz')
Die maximale Messabweichung beträgt: 1.0 Hz
Bei ganz niedrigen Frequenzen wird deshalb die Periodendauer gemessen, also z.B. von einem Nulldurchgang zum nächsten.
Bemerkung
Macht euch vorher Gedanken darüber, welche signifikanten Messabweichungen auftreten können, wenn ihr in bestimmten Frequenzbereichen Messungen vornehmt. Wählt eine sinnvolle Messzeit!
Zeitmessung#
Ähnlich zur Frequenzmessung können auch Zeitdauern gemessen werden. Das Prinzip ist das gleiche, nur sind Referenzquelle und Messung am Eingang der Torschaltung quasi vertauscht. Statt einer stabilen Referenzzeit an einem Eingang der Torschaltung, die bei der Frequenzmessung die Messzeit definiert hat, wird nun eine Referenzfrequenz angelegt. Die Frequenz wählt man so, dass die Anzahl der gezählten Pulse direkt die Messzeit in z.B. Millisekunden ausgibt. Wählt man als Referenzfrequenz beispielsweise \(f_r = 10\,\mathrm{kHz}\) und zählt 1400 Pulse, so erhält man eine gemessenen Zeit von
Der Restfehler basiert auf Zählfehlern, wie schon bei der Frequenzmessung.


