Kennlinie & Empfindlichkeit

Jede einzelne der Komponenten führt die an ihr anliegenden Eingangssignal in Ausgangssignale über. Wie diese Überführung genau aussieht beschreibt die sogenannte Kennlinie, die für jede Komponente unterschiedlich aussehen kann. In Abb. 26 ist beispielhaft eine lineare, ideale Kennlinie dargestellt.

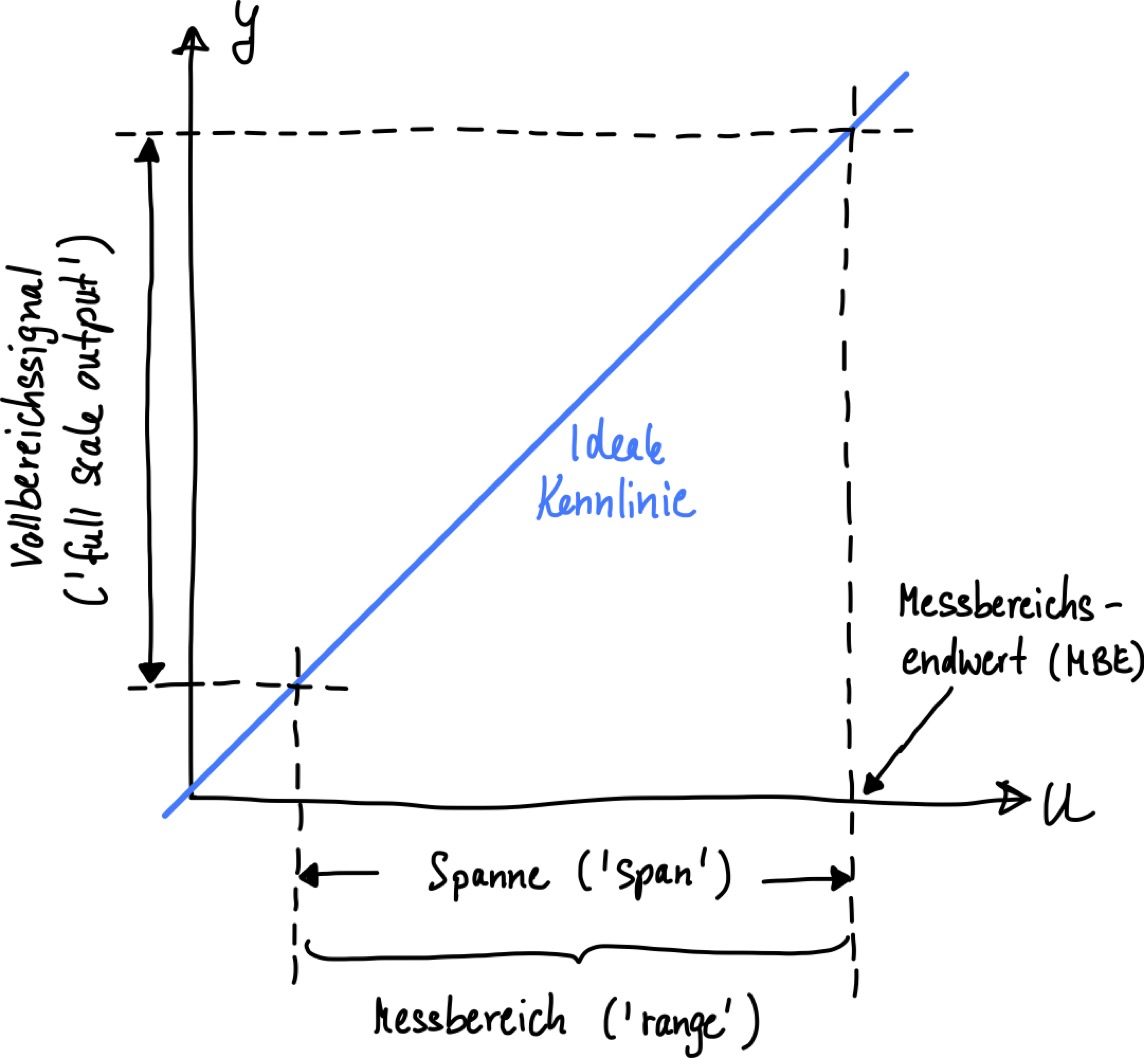
Abb. 26 Ideale Messkennlinie.

Statische Kenngrößen

Für jede Eingangsgröße \(u\) wird anhand der Kennlinie eine Ausgangsgröße \(y\) definiert. Beispielsweise wird anhand der Kennlinie eines Temperatursensors ein bestimmter Temperaturwert in eine Spannung umgewandelt.

• Der Bereich, indem der Sensor beispielsweise noch korrekt arbeitet (meist vom Hersteller garantiert) wird Messbereich (engl. range) genannt und wird durch den minimal und maximal möglichen Wert, der noch als Eingang angelegt werden kann oder darf, angegeben. Im Falle eines Temperatursensors wäre ein typischer Messbereich z.B. -40°C bis 120°C.

• Die Differenz zwischen diesen Maximal- und Minimalwert nennt man Spanne (engl. span) (bezogen auf unser Beispiel also 160°C).

• Die Spanne ist mit einem Bereich auf der y-Achse korreliert, nämlich dem sogenannten Vollbereichssignal (engl. full scale output = FSO).

• Der Übertragungsfaktor \(k\) oder auch oft Verstärkung genannt beschreibt die Überführung des Eingangssignals der Messeinrichtung, also der Messgröße, in ein Ausgangssignal:

\[y = k \cdot u\]

• Die Statische Kennlinie ist im Prinzip der Übertragungsfaktor, aber dieses Mal definiert für alle möglichen Eingangssignale.

\[y(u) = k \cdot u\]

Empfindlichkeit

Die Kennlinie sollte immer eine gewisse Steigung aufweisen. Oder man könnte auch sagen, dass wenn sich die Eingangsgröße \(u\) ändert, dass dies auch immer eine Änderung in der Ausgangsgröße \(y\) mit sich ziehen sollte. Im Falle einer Verstärkungseinheit könnte diese Änderung sogar vergrößert werden und das System reagiert somit empfindlicher auf Änderungen der Eingangsgröße. Mathematisch betrachtet bedeutet die Steilheit nichts anderes als die Steigung bzw. die Ableitung der Ausgangsgröße \(y(u)\) an einer bestimmten Stelle \(u\):

\[S(u) = \frac{\partial y(u)}{\partial u} = \frac{\partial f(u)}{\partial u}\]

Dies wird auch die Empfindlichkeit \(S(u)\) genannt und entspricht der Tangente im Punkt \(u\). Bei einer Messeinrichtung mit linearer Kennlinie sind die Empfindlichkeit \(S\) und die Übertragungsfunktion \(k\) demzufolge identisch.

Kennlinienbeispiele

Widerstandsthermometer

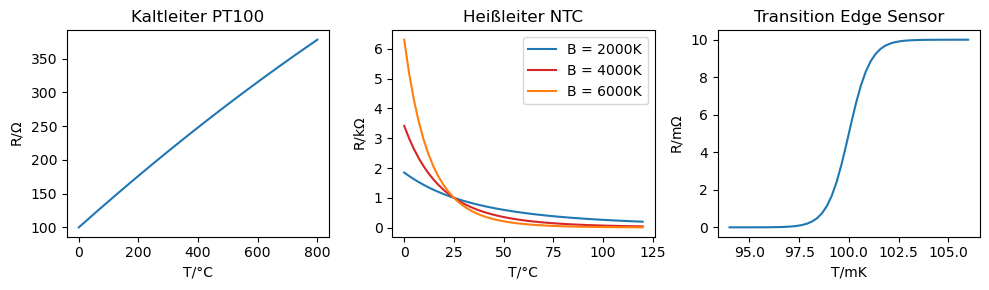
Reine Metalle sind Kaltleiter. Platin hat beispielsweise einen Widerstandswert von R0 = R(0) = 100 Ohm bei 0 °C, daher der Name PT100. Sie können bei geeigneter Ausrüstung bis 850 °C eingesetzt werden. Sie haben eine fast lineare Kennlinie bei einer relativen Widerstandsänderung von knapp 0,4 % pro °C:

\[R(T) = R_0 \cdot (1 + AT + BT^2)\]

Folgende Parameter gelten für bestimmte Temperaturbereiche:

• 0-850°C: A= 3,9e-3/°C, B=-5,7e-7/°C\(^2\)

• -200-0°C: C = -4,2e-1/°C\(^4\)

Thermistoren mit negativen Temperaturkoeffizienten (NTC = Negative thermal coefficient , Heißleiter) weisen aufgrund des zugrundeliegenden Halbleiter-Effektes eine hohe Abhängigkeit von Fehlstellen, wie der Dotierung der Grundstoffe auf. Heißleiter sind bis etwa 150 °C einsetzbar. Sie weisen gegenüber Platin-Messwiderständen eine deutlich höhere Empfindlichkeit auf:

\[ R(T)=R_{25} \cdot \mathrm e^{B\left(\frac{1}{T+273}-\frac{1}{298}\right)}\]

mit R25 = 1000 Ohm und B = 3528.

Ein Transition Edge Sensor (TES), bzw. auf deutsch Phasenübergangsthermometer, ist ein supraleitender Temperatursensor, der in der Lage ist, kleinste Temperaturänderungen im Bereich von wenigen 100 \(\mu\mathrm K\) zu messen. Seine Umgebungstemperatur wird je nach Material auf wenige mK runtergekühlt, um das Material in einen supraleitenden Zustand (d.h. sein Widerstand verschwindet) zu bringen. Dies ist die sogenannte kritische Temperatur, \(T_c\), aber der Materiale supraleitende Eigenschaften aufweisen. Der Widerstand wird über Anlegen einer Stromstärke minimal aufgeheizt, sodass sein Arbeitspunkt in den Übergang (die steile Flanke) geschoben wird. An diesem Punkt ist die Ableitung, und somit die Empfindlichkeit, maximal.

\[ R(T)= \frac{a}{1 + \mathrm e^{-k(T-T_c)}} \]

mit z.B. \(k\) = 1.86/mK, \(a\) = 0.224 Ohm und \(T_c\) = 103.2 mK

Show code cell source Hide code cell source

#Benötigte Libraries:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
import time
import warnings
warnings.filterwarnings('ignore')

# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße

#--------- Kaltleiter PT100 -------------
T_PT = np.linspace(0, 800, num=800)
def R_PT(T_PT):
    R_0 = 100 # in Ohm
    A = 3.93e-3 # in 1/°C
    B = -5.7e-7 # in 1/^C^2
    return R_0 * (1 + A*T_PT + B * T_PT**2)

#--------- Heißleiter NTC -------------
T_NTC = np.linspace(0+273.15, 120+273.15, num=50)
def R_NTC(T_NTC, B):
    R_25 = 1000 # in Ohm
    T_25 = 25.0 + 273.15 # in Kelvin
    return R_25 * np.exp(B * (1/(T_NTC) - 1/T_25))

#--------- Transition Edge Sensor -------------
T = np.linspace(94, 106, num=50)
def R(T):
    k = 1.86 # in 1/mK
    a = 0.01 # in Ohm
    Tk = 100 # in mK
    return a / (1+ np.exp(-k * (T-Tk)))


#--------- Diagramme -------------
f, axs = plt.subplots(1,3,figsize=(10,3))

axs[0].plot(T_PT,R_PT(T_PT), color = 'tab:blue')
axs[0].set_xlabel('T/°C')
axs[0].set_ylabel(r'R/$\Omega$')
axs[0].set_title('Kaltleiter PT100')

axs[1].plot(T_NTC-273.15,R_NTC(T_NTC, 2000)/1000, label = "B = 2000K", color = 'tab:blue')
axs[1].plot(T_NTC-273.15,R_NTC(T_NTC, 4000)/1000, label = "B = 4000K", color = 'tab:red')
axs[1].plot(T_NTC-273.15,R_NTC(T_NTC, 6000)/1000, label = "B = 6000K", color = 'tab:orange')
axs[1].set_xlabel('T/°C')
axs[1].set_ylabel(r'R/k$\Omega$')
axs[1].set_title('Heißleiter NTC')
axs[1].legend()

axs[2].plot(T,R(T)*1000, color = 'tab:blue')
axs[2].set_xlabel('T/mK')
axs[2].set_ylabel(r'R/m$\Omega$')
axs[2].set_title('Transition Edge Sensor')

plt.tight_layout()
plt.show()

Laserinterferometer

Michelson - Interferometer, Aufbau und Messung | Physik - Experimente & Formeln - Matthias Kohl

Siehe auch

Wie funktioniert Laserinterferometerie?

Laserinterferometer sind extrem empfindliche Messinstrumente und in modernen Messaufbauten fast immer vorhanden, wenn Längenänderungen, Geschwindikeiten oder Beschleunigungen gemessen werden soll.

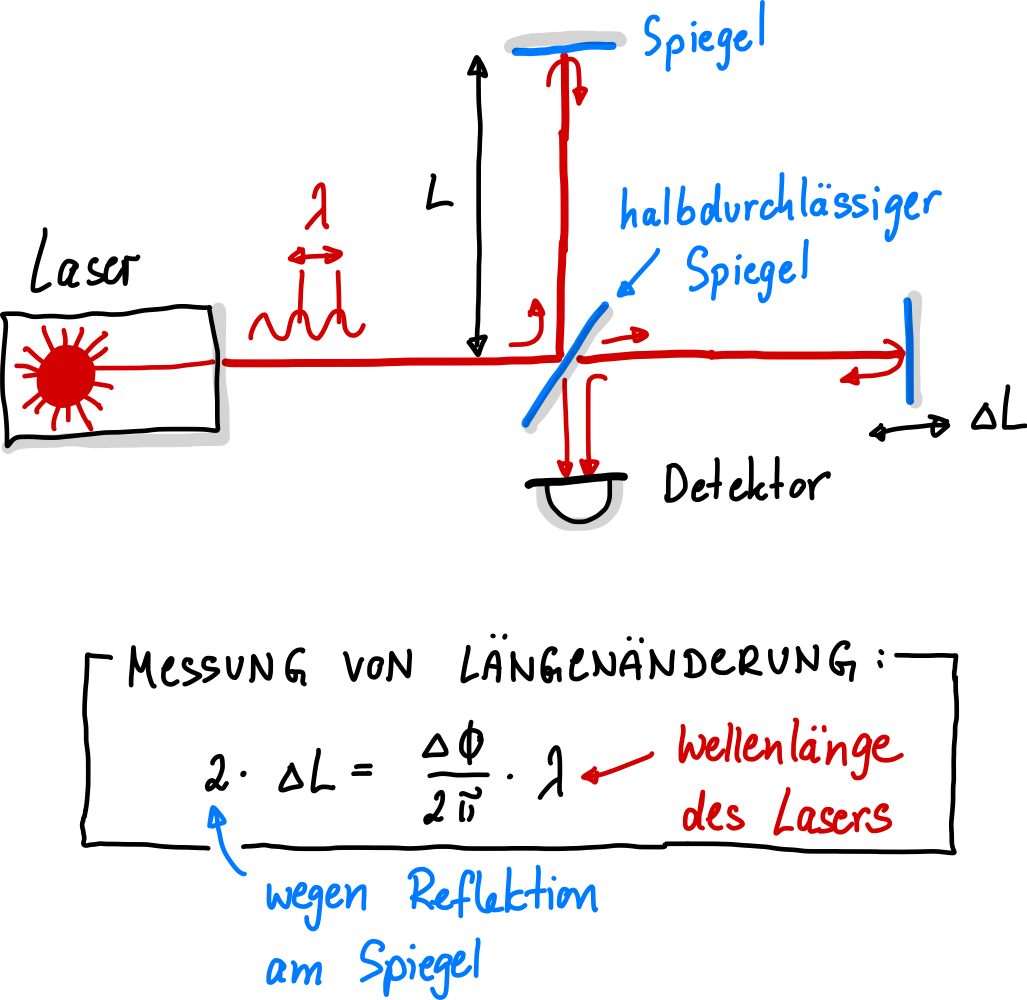
Abb. 27 Laserinterferometer.

In einem Interferometer werden Längen durch die Messung von Phasenverschiebungen von zwei interferierenden elektromagnetischen Wellen (Laser) bestimmt. Die Phasenverschiebung ist direkt mit der Weglängendifferenz zwischen den beiden Wellen verbunden

\[ 2 \cdot \Delta L = \left( \frac{\Delta \phi}{2\pi} \right) \cdot \lambda \]

• \(\Delta L\) ist die Weglängendifferenz,

• \( \Delta \phi\) ist die Phasenverschiebung in Radiant,

• \( \lambda \) ist die Wellenlänge des Lichts.

Der Faktor 2 resultiert daraus, dass in Interferometern der Laserstrahl reflektiert wird und somit die Weglängendifferenz 2x durchläuft. Dies erhöht die Auflösung der Messung um den Faktor 2. Wenn wir die Phasenverschiebung und die Wellenlänge kennen, können wir die Weglängendifferenz berechnen, die einer Längenänderung entspricht. Die Wellenlänge ist für Laser extrem genau bekannt. Wie erhält man jedoch die Phaseninformation? Bei der Interferenz (Überlagerung) von den beiden Laserstrahlen am Strahlteiler entsteht ein Interferenzmuster. Eine Fotodiode ist in der Lage, die Intensität der Laserstrahlen zu messen, welche proportional zu Quadrat der beiden Laserwellen \(E_1\) und \(E_2\) ist:

\[I(x,t) = |E_1 + E_2|^2 = ... = E_0^2 \cdot (1 + \cos(\Delta \phi))\]

Herleitung der interferometerischen Intensität

Die elektrischen Felder der beiden Wellen entlang der beiden Interferometerarme sind gegeben durch:

\[ E_1(x,t) = E_0 \cdot \cos(kx - \omega t + \phi_1) \]

\[ E_2(x,t) = E_0 \cdot \cos(kx - \omega t + \phi_2) \]

Hierbei ist:

• \(E_0\) die Amplitude des elektrischen Feldes,

• \(k\) die Wellenzahl (\(k = \frac{2\pi}{\lambda}\), wobei \(\lambda\) die Wellenlänge ist),

• \(\omega\) die Winkelgeschwindigkeit \((\omega = 2\pi f\), wobei \(f\) die Frequenz ist),

• \(\phi_1\) und \(\phi_2\) sind die Phasen der beiden Wellen,

• \(x\) ist der Ort entlang der Ausbreitungsrichtung,

• \(t\) ist die Zeit.

Die Summe dieser beiden Felder ergibt das resultierende elektrische Feld \( E \):

\[ E(x,t)= E_1(x,t) + E_2(x,t) = E_0 \cdot \cos(kx - \omega t + \phi_1) + E_0 \cdot \cos(kx - \omega t + \phi_2) \]

Die Intensität \(I\) des resultierenden Feldes ist proportional zum Quadrat des Betrags des elektrischen Feldes:

\[\begin{align*} I(x,t) &= |E(x,t)|^2 = |E_0 \cdot \cos(kx - \omega t + \phi_1) + E_0 \cdot \cos(kx - \omega t + \phi_2)|^2 \\ &= ... = E_0^2 \cdot (1 + \cos(\Delta \phi)) \end{align*}\]

Die resultierende Gleichung zeigt die Intensität der Interferenz in Abhängigkeit von der Phasendifferenz zwischen den beiden Wellen.

Die Ausgangsintensität variiert sinusförmig mit der Phasenverschiebung! Die Kennlinie ist also nicht ideal, bzw. nur in einem winzigen ausgewählten Bereich an den Wendepunkten.

Die Empfindlichkeit des Interferometers – also seine Fähigkeit, kleine Änderungen zu detektieren – ist an den Wendepunkten der sinusförmigen Kurve am höchsten (hier ist die Ableitung maximal). An den Extrempunkten ist die Empfindlichkeit null, da hier kleine Änderungen der Phasenverschiebung fast keine Änderung im Ausgangssignal bewirken (Ableitung verschwindet).

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.widgets import Slider
from matplotlib.animation import FuncAnimation
from IPython.display import HTML
plt.rcParams['font.size'] = 10; # Schriftgröße


# Initialisierung des Plots und der Achsen
fig, ax = plt.subplots(figsize=(5, 3), tight_layout=True)


# Berechnung der Intensität in Abhängigkeit von der Phasenverschiebung
def calculate_interferometer_signal(phase_difference):
    intensity = 0.5*(1+np.cos(phase_difference / 2.0))
    return intensity



# Aktualisierungsfunktion für den Slider
def update(val):
    phase_difference = np.linspace(0, 8 * np.pi, 1000)

    intensity = calculate_interferometer_signal(phase_difference+val)
    
    ax.plot(phase_difference, calculate_interferometer_signal(phase_difference), color='tab:blue', lw=4, alpha=0.5, label='in Ruhe')
    ax.plot(phase_difference, intensity, color='tab:red', label='Bewegung =%5.2f rad =%5.2f $\mu$m'%(val, (val)/(4*np.pi)))
    # Set plot labels and legend
    #ax.set_title('Analog zeitdiskret: Abgetastete Sinuswelle')
    ax.set_xlabel('Phasenverschiebung (rad)')
    ax.set_ylabel('Intensität')
    ax.set_ylim([0, 1])
    ax.set_xlim([0, 8 * np.pi])
    ax.grid(True)
    ax.legend(loc='lower left')
    ax.set_title(r'Laserinterferometer mit Wellenlänge $1\,\mathrm{\mu m}$')

# Funktion zur Aktualisierung der Animation
def animate(val):
    ax.clear()
    update(val)

# Create an animation by varying reflectivity from 0.01 to 0.99 with a step of 0.01
ani = FuncAnimation(fig, animate, frames=np.arange(0.0, 3*np.pi, 0.1), repeat=False)

# Anzeigen der Animation
#plt.tight_layout()
plt.close()
HTML(ani.to_jshtml())
# Create an animation by varying reflectivity from 0.01 to 0.99 with a step of 0.01
ani = FuncAnimation(fig, animate, frames=np.arange(0.0, 3*np.pi, 0.1), repeat=False)

# Save the animation as an MP4 file with higher resolution
ani.save('phase_shift_laserifo.mp4', writer='ffmpeg', dpi=600)

# Anzeigen der Animation
#plt.tight_layout()
plt.close()
HTML(ani.to_jshtml())

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In[2], line 59
     56 # Anzeigen der Animation
     57 #plt.tight_layout()
     58 plt.close()
---> 59 HTML(ani.to_jshtml())

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/animation.py:1353, in Animation.to_jshtml(self, fps, embed_frames, default_mode)
   1349         path = Path(tmpdir, "temp.html")
   1350         writer = HTMLWriter(fps=fps,
   1351                             embed_frames=embed_frames,
   1352                             default_mode=default_mode)
-> 1353         self.save(str(path), writer=writer)
   1354         self._html_representation = path.read_text()
   1356 return self._html_representation

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/animation.py:1109, in Animation.save(self, filename, writer, fps, dpi, codec, bitrate, extra_args, metadata, extra_anim, savefig_kwargs, progress_callback)
   1107         progress_callback(frame_number, total_frames)
   1108         frame_number += 1
-> 1109 writer.grab_frame(**savefig_kwargs)

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/animation.py:775, in HTMLWriter.grab_frame(self, **savefig_kwargs)
    773     return
    774 f = BytesIO()
--> 775 self.fig.savefig(f, format=self.frame_format,
    776                  dpi=self.dpi, **savefig_kwargs)
    777 imgdata64 = base64.encodebytes(f.getvalue()).decode('ascii')
    778 self._total_bytes += len(imgdata64)

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/figure.py:3390, in Figure.savefig(self, fname, transparent, **kwargs)
   3388     for ax in self.axes:
   3389         _recursively_make_axes_transparent(stack, ax)
-> 3390 self.canvas.print_figure(fname, **kwargs)

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/backend_bases.py:2187, in FigureCanvasBase.print_figure(self, filename, dpi, facecolor, edgecolor, orientation, format, bbox_inches, pad_inches, bbox_extra_artists, backend, **kwargs)
   2183 try:
   2184     # _get_renderer may change the figure dpi (as vector formats
   2185     # force the figure dpi to 72), so we need to set it again here.
   2186     with cbook._setattr_cm(self.figure, dpi=dpi):
-> 2187         result = print_method(
   2188             filename,
   2189             facecolor=facecolor,
   2190             edgecolor=edgecolor,
   2191             orientation=orientation,
   2192             bbox_inches_restore=_bbox_inches_restore,
   2193             **kwargs)
   2194 finally:
   2195     if bbox_inches and restore_bbox:

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/backend_bases.py:2043, in FigureCanvasBase._switch_canvas_and_return_print_method.<locals>.<lambda>(*args, **kwargs)
   2039     optional_kws = {  # Passed by print_figure for other renderers.
   2040         "dpi", "facecolor", "edgecolor", "orientation",
   2041         "bbox_inches_restore"}
   2042     skip = optional_kws - {*inspect.signature(meth).parameters}
-> 2043     print_method = functools.wraps(meth)(lambda *args, **kwargs: meth(
   2044         *args, **{k: v for k, v in kwargs.items() if k not in skip}))
   2045 else:  # Let third-parties do as they see fit.
   2046     print_method = meth

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/backends/backend_agg.py:497, in FigureCanvasAgg.print_png(self, filename_or_obj, metadata, pil_kwargs)
    450 def print_png(self, filename_or_obj, *, metadata=None, pil_kwargs=None):
    451     """
    452     Write the figure to a PNG file.
    453 
   (...)
    495         *metadata*, including the default 'Software' key.
    496     """
--> 497     self._print_pil(filename_or_obj, "png", pil_kwargs, metadata)

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/backends/backend_agg.py:445, in FigureCanvasAgg._print_pil(self, filename_or_obj, fmt, pil_kwargs, metadata)
    440 def _print_pil(self, filename_or_obj, fmt, pil_kwargs, metadata=None):
    441     """
    442     Draw the canvas, then save it using `.image.imsave` (to which
    443     *pil_kwargs* and *metadata* are forwarded).
    444     """
--> 445     FigureCanvasAgg.draw(self)
    446     mpl.image.imsave(
    447         filename_or_obj, self.buffer_rgba(), format=fmt, origin="upper",
    448         dpi=self.figure.dpi, metadata=metadata, pil_kwargs=pil_kwargs)

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/backends/backend_agg.py:388, in FigureCanvasAgg.draw(self)
    385 # Acquire a lock on the shared font cache.
    386 with (self.toolbar._wait_cursor_for_draw_cm() if self.toolbar
    387       else nullcontext()):
--> 388     self.figure.draw(self.renderer)
    389     # A GUI class may be need to update a window using this draw, so
    390     # don't forget to call the superclass.
    391     super().draw()

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/artist.py:95, in _finalize_rasterization.<locals>.draw_wrapper(artist, renderer, *args, **kwargs)
     93 @wraps(draw)
     94 def draw_wrapper(artist, renderer, *args, **kwargs):
---> 95     result = draw(artist, renderer, *args, **kwargs)
     96     if renderer._rasterizing:
     97         renderer.stop_rasterizing()

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/artist.py:72, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     69     if artist.get_agg_filter() is not None:
     70         renderer.start_filter()
---> 72     return draw(artist, renderer)
     73 finally:
     74     if artist.get_agg_filter() is not None:

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/figure.py:3154, in Figure.draw(self, renderer)
   3151         # ValueError can occur when resizing a window.
   3153 self.patch.draw(renderer)
-> 3154 mimage._draw_list_compositing_images(
   3155     renderer, self, artists, self.suppressComposite)
   3157 for sfig in self.subfigs:
   3158     sfig.draw(renderer)

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/image.py:132, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    130 if not_composite or not has_images:
    131     for a in artists:
--> 132         a.draw(renderer)
    133 else:
    134     # Composite any adjacent images together
    135     image_group = []

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/artist.py:72, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     69     if artist.get_agg_filter() is not None:
     70         renderer.start_filter()
---> 72     return draw(artist, renderer)
     73 finally:
     74     if artist.get_agg_filter() is not None:

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/axes/_base.py:3070, in _AxesBase.draw(self, renderer)
   3067 if artists_rasterized:
   3068     _draw_rasterized(self.figure, artists_rasterized, renderer)
-> 3070 mimage._draw_list_compositing_images(
   3071     renderer, self, artists, self.figure.suppressComposite)
   3073 renderer.close_group('axes')
   3074 self.stale = False

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/image.py:132, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    130 if not_composite or not has_images:
    131     for a in artists:
--> 132         a.draw(renderer)
    133 else:
    134     # Composite any adjacent images together
    135     image_group = []

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/artist.py:72, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     69     if artist.get_agg_filter() is not None:
     70         renderer.start_filter()
---> 72     return draw(artist, renderer)
     73 finally:
     74     if artist.get_agg_filter() is not None:

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/axis.py:1394, in Axis.draw(self, renderer, *args, **kwargs)
   1391     tick.draw(renderer)
   1393 # Shift label away from axes to avoid overlapping ticklabels.
-> 1394 self._update_label_position(renderer)
   1395 self.label.draw(renderer)
   1397 self._update_offset_text_position(tlb1, tlb2)

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/axis.py:2609, in YAxis._update_label_position(self, renderer)
   2605     return
   2607 # get bounding boxes for this axis and any siblings
   2608 # that have been set by `fig.align_ylabels()`
-> 2609 bboxes, bboxes2 = self._get_tick_boxes_siblings(renderer=renderer)
   2610 x, y = self.label.get_position()
   2611 if self.label_position == 'left':

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/axis.py:2160, in Axis._get_tick_boxes_siblings(self, renderer)
   2158 for ax in grouper.get_siblings(self.axes):
   2159     axis = ax._axis_map[name]
-> 2160     ticks_to_draw = axis._update_ticks()
   2161     tlb, tlb2 = axis._get_ticklabel_bboxes(ticks_to_draw, renderer)
   2162     bboxes.extend(tlb)

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/axis.py:1306, in Axis._update_ticks(self)
   1304         pass
   1305     else:
-> 1306         if mtransforms._interval_contains_close(interval_t, loc_t):
   1307             ticks_to_draw.append(tick)
   1309 return ticks_to_draw

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/transforms.py:2919, in _interval_contains_close(interval, val, rtol)
   2897 def _interval_contains_close(interval, val, rtol=1e-10):
   2898     """
   2899     Check, inclusively, whether an interval includes a given value, with the
   2900     interval expanded by a small tolerance to admit floating point errors.
   (...)
   2917         Whether *val* is within the *interval* (with tolerance).
   2918     """
-> 2919     a, b = interval
   2920     if a > b:
   2921         a, b = b, a

KeyboardInterrupt: 

Die Empfindlichkeit von Laserinterferometern kann mittels optischen Resonatoren enorm gesteigert werden. Dafür baut man in dem Interferometer weitere Spiegel mit bestimmten Reflektivitäten ein, die das Licht auf der Wegstrecke einfangen. Dadurch wird die Strecke künstlich länger gemacht. Da das Licht nun mehrere Male an dem sich bewegenden Objekt reflektiert wird, wird die Positionsänderung mehrere Male gemessen, was man als Empfindlichkeitssteigerung interpretieren kann. Die Kennlinie zeigt den Effekt noch mal deutlicher.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML
plt.rcParams['font.size'] = 10; # Schriftgröße


# Initialize the figure and axis
fig, ax = plt.subplots(figsize=(5, 3), tight_layout=True)


# Funktion zur Berechnung der Intensität in Abhängigkeit von der Phasenverschiebung
def calculate_intensity(reflectivity, phase_difference):
    finesse = np.pi * reflectivity / (1 - reflectivity)
    intensity = 1 / (1 + finesse * np.sin(phase_difference / 2.0)**2)
    return intensity

# Funktion zum Aktualisieren der Grafik
def update(reflectivity):
    x = np.linspace(0, 6 * np.pi, 1000)  # Phasenverschiebung von 0 bis 6*pi
    phase_difference = x
    intensity = calculate_intensity(reflectivity, phase_difference)
    
    ax.plot(phase_difference, calculate_intensity(0.9, phase_difference), color='tab:blue', lw=4, alpha=0.5, label='Resonator Reflektivität: R = 0.9')
    ax.plot(phase_difference, intensity, color='tab:red', label='Resonator Reflektivität: R =%5.2f'%(reflectivity))
    # Set plot labels and legend
    #ax.set_title('Analog zeitdiskret: Abgetastete Sinuswelle')
    ax.set_xlabel('Phasenverschiebung (rad)')
    ax.set_ylabel('Intensität')
    ax.set_ylim([0, 1])
    ax.grid(True)
    ax.legend(loc='upper right')


# Funktion zur Aktualisierung der Animation
def animate(reflectivity):
    ax.clear()
    update(reflectivity)

# Create an animation by varying reflectivity from 0.01 to 0.99 with a step of 0.01
ani = FuncAnimation(fig, animate, frames=np.arange(0.01, 0.999, 0.01), repeat=False)

ani.save('laser_resonator_empfindlichkeit.mp4', writer='ffmpeg', dpi=600)


# Anzeigen der Animation
#plt.tight_layout()
plt.close()
HTML(ani.to_jshtml())

Once Loop Reflect

Je nach Reflektivität der Spiegel, wird die Kennlinie stellenweise extrem steil, das heißt die Ableitung (= Empfindlichkeit) extrem groß. Man erkennt allerdings auch den Nachteil von sehr hohen Empfindlichkeiten: Der Messbereich wird sehr klein. Sollte sich die Länge nun sehr stark ändern, so kann dies von diesem Messinstrument nicht mehr aufgelöst werden. Anders ausgedrückt: Das Laserinterferometer an sich muss extrem ruhig sein und die Spiegel dürfen sich nur noch minimal bewegen.

Siehe auch

Mehr zur Laserinterferometrie und optischen Resonatoren findest du hier.

Schlussfolgerung

Wir sehen ins unseren Beispielen, dass Kennlinien in den seltensten Fällen von Natur aus ideal sind. Was also tun?