Messung von Kapazitäten und Induktivitäten#

Manche Sensoren ändern ihr kapazitives oder induktives Verhalten aufgrund der Messgröße \(x\). Das Auslesen diese Änderung basiert auf den gleichen Verfahren, die wir schon im Kapitel Widerstandsmessungen kennen gelernt haben. Jedoch müssen wir jetzt mit Wechselspannungen arbeiten, da Kapazität oder Induktivität ansonsten nicht existieren. Fast ausschließlich werden wir hierfür ein Sinussignal ohne Gleichanteil verwenden. Um die Kapazität \(C\) bzw. Induktivität \(L\) zu bestimmen, wird wieder eine gleichzeitige Messung von Strom und Spannung benötigt, bzw. deren Effektivwerten!

Stromrichtige und spannungsrichtige Anschaltung#

Abb. 105 zeigt wie man Kapazität bzw. Induktivität direkt messen kann in dem Spannungs und Strom gemessen werden.

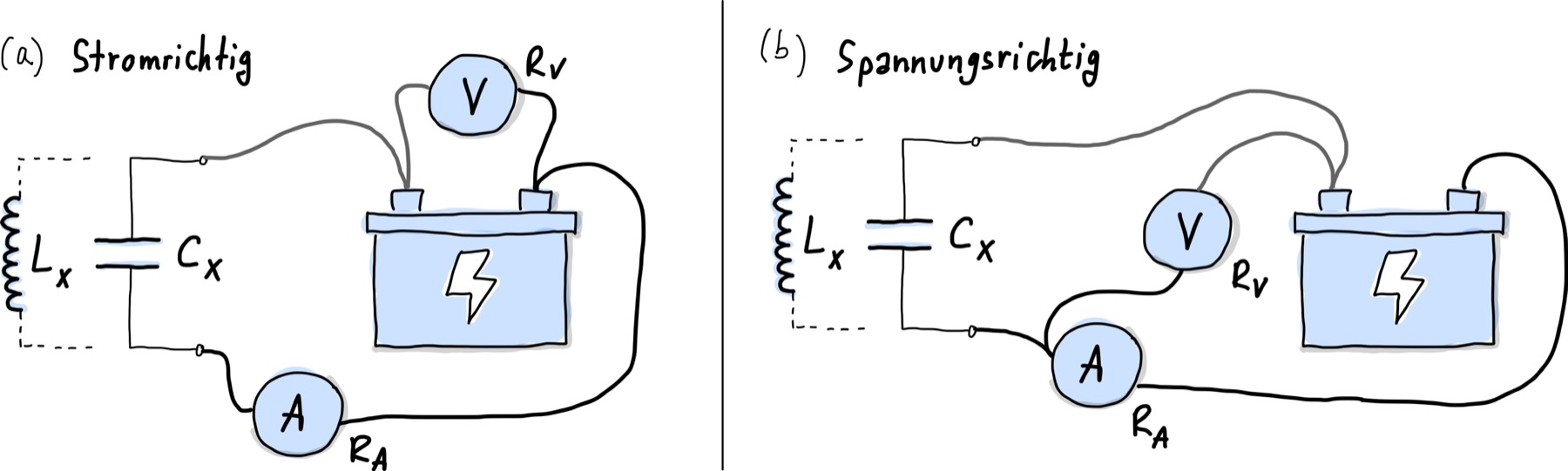
CL_stromspannungsrichtig

Abb. 105 Schaltung zur Messung von Kapazitäten, bzw. Induktivitäten. Links ist die spannungsrichtige Anschaltung gezeigt, rechts die stromrichtige.#

Mit beiden Messeingängen werden die Effektivwerte \(u_\mathrm{eff}\) und \(i_\mathrm{eff}\) ermittelt. Aus dem Blindwiderstand,

\[X = \frac{u_\mathrm{eff}}{i_\mathrm{eff}}\]

können Kapazität und Induktivität bestimmt werden:

  • Kapazität:

\[X_{C_x} = \frac{1}{\omega C_x} = \frac{1}{2\pi f C_x} \Rightarrow C_x = \frac{1}{\omega X_{C_x}} = \frac{i_\mathrm{eff}}{\omega \cdot u_\mathrm{eff}}\]

  • Induktivität:

\[X_{L_x} = \omega L_x = 2\pi f L_x \Rightarrow L_x = \frac{X_{L_x}}{\omega} = \frac{u_\mathrm{eff}}{\omega \cdot i_\mathrm{eff}}\]

Neben den Effektivwerten wird noch die Frequenz benötigt, die entweder als konstant angenommen wird oder, wenn man es genauer wissen möchte, gemessen wird wie in Kapitel Frequenzmessung. Auf die Herleitung der Messabweichung bei strom- bzw. spannungsrichtiger Anschaltung wollen wir dieses mal verzichten. Es gilt die gleiche Auswertung wie in Kapitel Widerstandsmessungen.

Induktiver Verlustwiderstand#

Eine weitere Unsicherheit, die es so bei ohmschen Widerständen nicht gab, ist der Verlustwiderstand der Spule, der aufgrund der Spulenwicklung existiert. Der hierbei entstehende Verlustwiderstand kann bis zu \(100\,\Omega\) annehmen und wir können nicht mehr das einfach ohm’sche Gesetz für Blindwiderstände benutzen und müssen in die komplexe Schreibweise wechseln. Für den Widerstand gilt also nun, dass er einen Realteil (der ohmsche Widerstand) und einen Imaginärteil aufweist:

\[X_L = R_L + j \cdot \omega L_x = \frac{\underline u_\mathrm{eff}}{\underline i_\mathrm{eff}}\]

Die Effektivwerde sind mit einem Unterstrich gekennzeichnet um zu verdeutlichen, dass es sich hierbei um komplexe Zahlen handelt. \(R_L\) ist der ohmsche Widerstand, \(L_x\) ist die ideale Spule, welche in einem Ersatzschaltbild in Reihe geschaltet werden würden.

Von der obigen Formel bilden wir den Betrag und erhalten nach Umstellen für die Induktivität ein genaueres Ergebnis, wenn wir folgende Formel benutzen:

\[L_x = \frac{\sqrt{ \left( \frac{u_\mathrm{eff}}{i_\mathrm{eff}} \right)^2}-R_L^2 }{\omega}\]

Aufgabe

Beweise die Formel für die Induktion.

Diese Formel sollte prinzipiell benutzt werden. \(R_L\) erhält man aus dem Datenblatt der Spule oder durch eine zusätzliche Messung.

Messung mittels 2 Spannungsmessungen#

Wie auch schon bei Widerstandsmessungen können wir auf die ungenaue Strommessung verzichten, wenn uns eine Referenz-Kapazität bzw. -Induktivität zur Verfügung steht. Das Referenzelement muss hierbei einen festen Kapazitäts- bzw. Induktionswert aufweisen.

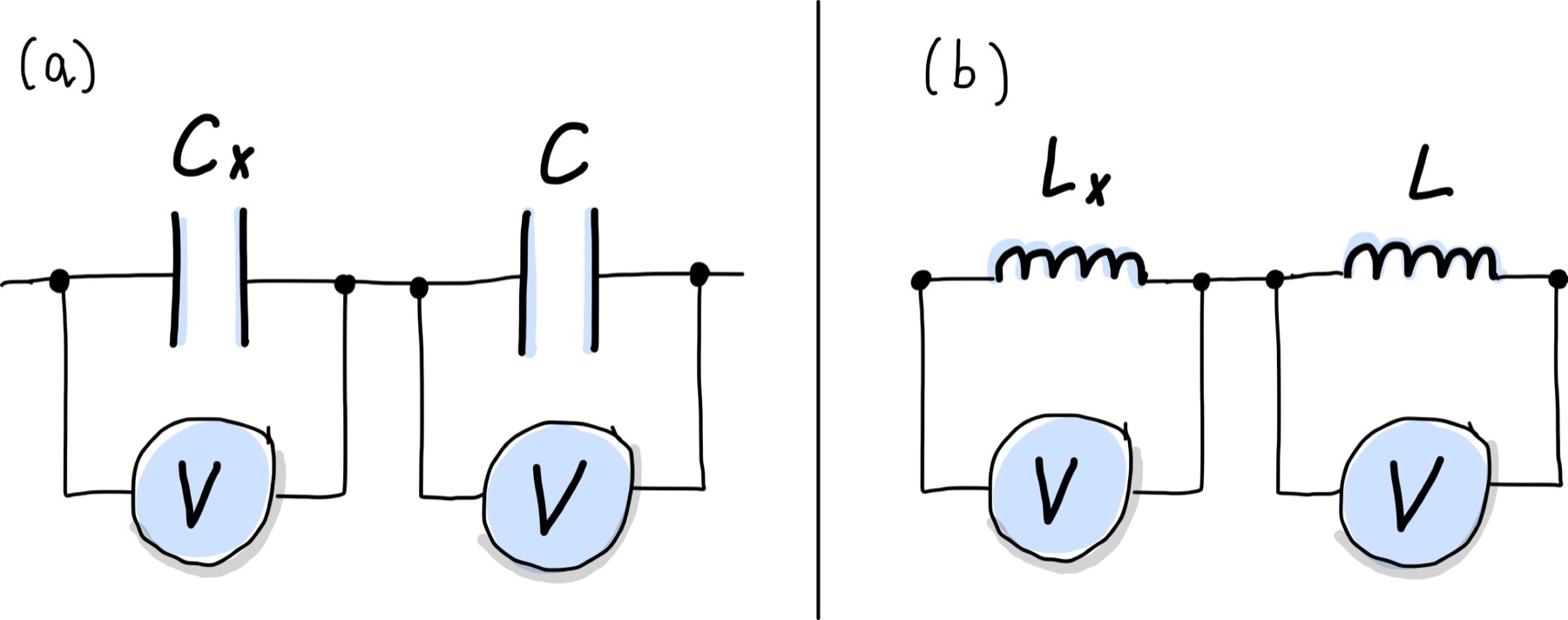
LC_2volt

Abb. 106 Schaltung zur Messung von Kapazitäten (links), bzw. Induktivitäten (rechts) mit 2 Spannungsmesseingängen.#

Die Spannung wird an beiden Elementen gemessen und der gesuchte Werte, \(C_x\) bzw. \(L_x\), können aus dem Spannungsverhältnis berechnet werden:

  • Kapazität:

\[\frac{u_{\mathrm{eff}}}{u_{{x,\mathrm{eff}}}} = \frac{\frac{1}{\omega C}}{\frac{1}{\omega C_x}} = \frac{C_x}{C} \Rightarrow C_x = C \cdot \frac{u_\mathrm{eff}}{u_{x,\mathrm{eff}}}\]

  • Induktivität:

\[\frac{u_{\mathrm{eff}}}{u_{{x,\mathrm{eff}}}} = \frac{\omega L}{\omega L_x} = \frac{L}{L_x} \Rightarrow L_x = L \cdot \frac{u_{x,\mathrm{eff}}}{u_\mathrm{eff}}\]

Die Messabweichung aufgrund der Innenwiderstände der Spannungsmesseingänge gelten auch hier.

Brückenschaltung#

Genauso wie für Widerstände können wieder verschiedene Brückenschaltungen benutzt werden um Kapazitäten und Induktivitäten zu messen um ggf. Störeffekte minimieren.

Viertelbrücke#

Abb. 107 zeigt die Viertelbrückenschaltung. Der Spannungsteiler, indem die zu messende Kapazität- bzw. Induktivitätsänderung ist, befindet sich außerdem ein zweites Element mit festem Wert. Der andere Spannungsteiler kann aus ohmschen Widerständen gebaut werden. Da die Messbrücke mit Wechselspannung betrieben wird, kann das Vorzeichen der Messgröße \(x\) nicht durch Umpolung umgekehrt werden.

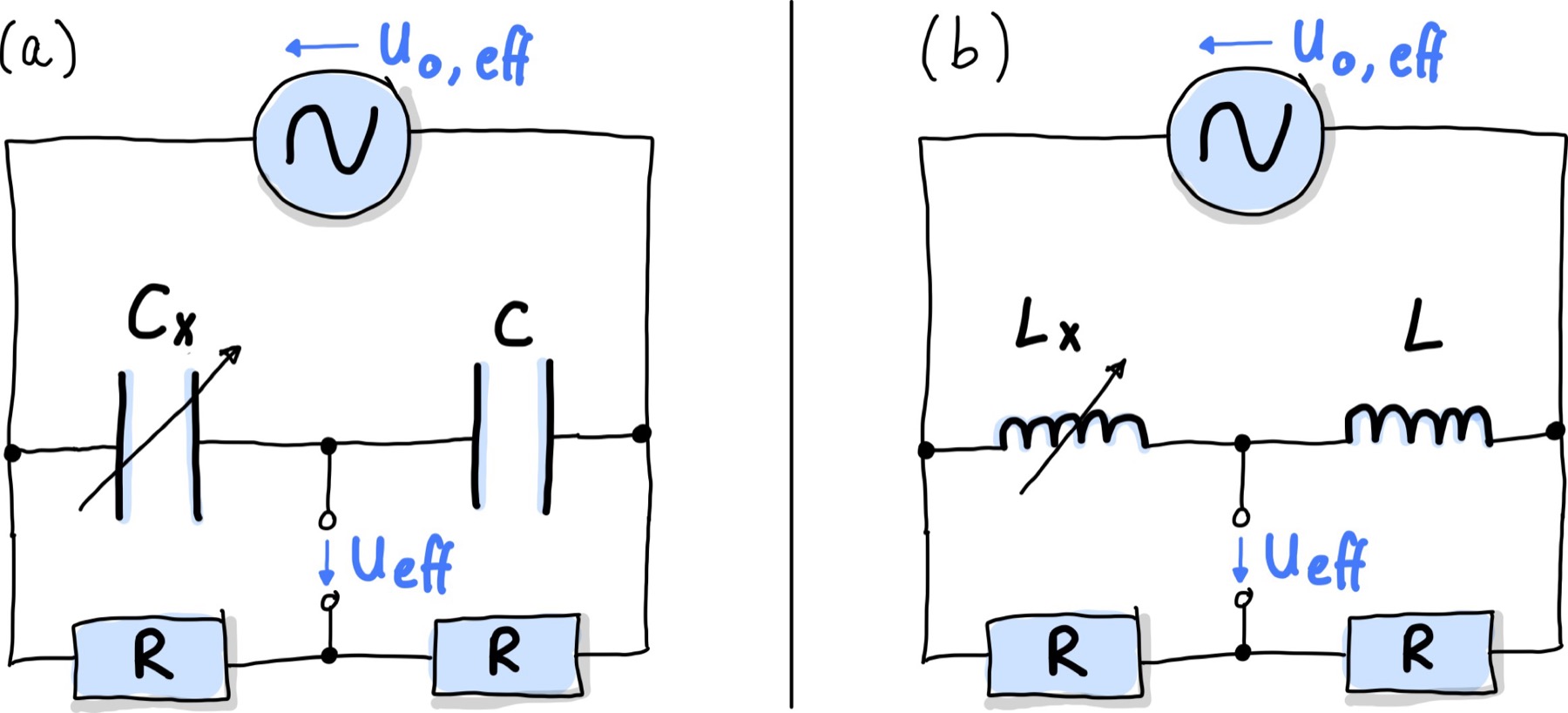
LC_viertel

Abb. 107 Schaltung zur Messung von Kapazitäten (links), bzw. Induktivitäten (rechts) mit einer Viertelbrücke.#

Für die Kennlinien erhalten wir ähnliche Ergebnisse, wie schon im Kapitel Widerstandsmessungen hergeleitet.

  • Kapazität:

\[C_x = C(x) = C + \Delta C(x) \]
\[\begin{split} \begin{align} \frac{u(x)_{\mathrm{eff}}}{u_{0,\mathrm{eff}}} &= \left| \frac{C}{C+C_x} - \frac{1}{2} \right| \\ &= \left| \frac{\Delta C(x)}{2 [2C + \Delta C(x)]} \right|\\ &\approx \frac{\left|\Delta C(x) \right|}{4C} \end{align} \end{split}\]

  • Induktivität:

\[L_x = L(x) = L + \Delta L(x)\]
\[\begin{split} \begin{align} \frac{u(x)_{\mathrm{eff}}}{u_{0,\mathrm{eff}}} &= \left| \frac{L_x}{L+L_x} - \frac{1}{2} \right| \\ &= \left| \frac{\Delta L(x)}{2[2L + \Delta L(x)]} \right| \\ &\approx \frac{\left|\Delta L(x) \right|}{4L} \end{align} \end{split}\]

Im letzten Schritt der Umformung wurde angenommen, dass sich die Messgröße nur wenig ändert, d.h. \(\left|\Delta C(x)\right|<<C\), bzw. \(\left|\Delta L(x)\right|<<L\).

Folgende Unterschiede und Anmerkungen sollten im Vergleich zur Brückenschaltung von rein ohmschen Komponenten erwähnt werden:

  • Beim Betrieb mit Wechselspannung geht das Vorzeichen der Messgröße verloren

  • Um das Vorzeichen zu bekommen muss die Phasenverschiebung zwischen Eingangs- und Ausgangssignal gemessen werden. Bei einer positiven Kapazitätsänderung \(\Delta C(x)\) wäre diese -180°.

Halbbrücke#

Um Störgrößen zu reduzieren können Kapazitäts- und Induktionsmessung in Halbbrücken integriert werden. Die anschaltung ist in Abb. 108 dargestellt.

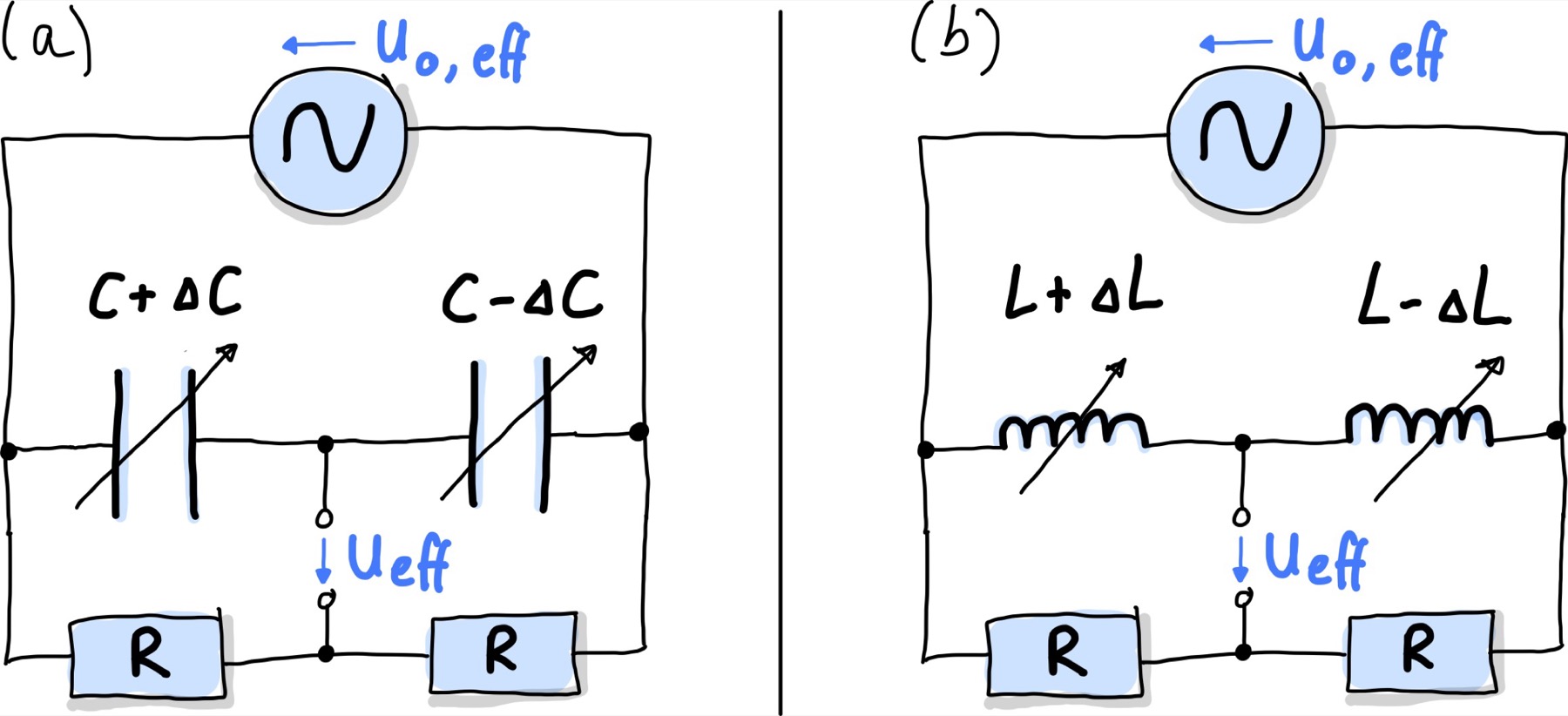
LC_halbbr

Abb. 108 Schaltung zur Messung von Kapazitäten (links), bzw. Induktivitäten (rechts) mit einer Halbbrücke.#

Die Herleitung der Kennlinien ist wieder analog zur Viertelbrücke, bzw. analog zur Widerstandsbrücke und liefert folgende Ergebnisse:

  • Kapazität:

\[ \frac{u(x)_{\mathrm{eff}}}{u_{0,\mathrm{eff}}} = \frac{\left|\Delta C(x) \right|}{2C} \]

  • Induktivität:

\[ \frac{u(x)_{\mathrm{eff}}}{u_{0,\mathrm{eff}}} = \frac{\left|\Delta L(x) \right|}{2L} \]

Unter dem Einfluss einer externen Störgröße, \(\Delta C(T)\) bzw. \(\Delta L(T)\), ergeben sich folgende Formeln, wobei im letzten Schritt wieder eine sehr kleine Änderung, \(\Delta C(T) << C\) bzw. \(\Delta L(T) << L\) angenommen wird, wodruch die Temperaturabhängigkeit wieder verschwindt (oder die Abhängigkeit zu einer anderen externen Größe):

  • Kapazität:

\[ \frac{u(x)_{\mathrm{eff}}}{u_{0,\mathrm{eff}}} = \frac{\left|\Delta C(x) \right|}{2[C + \Delta C(T)]} \approx \frac{\left|\Delta C(x) \right|}{2C} \]

  • Induktivität:

\[ \frac{u(x)_{\mathrm{eff}}}{u_{0,\mathrm{eff}}} = \frac{\left|\Delta L(x) \right|}{2[L + \Delta L(T)]} \approx \frac{\left|\Delta L(x) \right|}{2L} \]

Vollbrücken#

Vollbrücken werden bei Kapazitäts- bzw. Induktivitätsmessungen eigentlich nicht verwendet. Bereits unterschiedliche Kabellängen verursachen starke Messabweichungen, da die verursachten Kapazität- und Induktivitätsbeiträge in der Schaltung wirken. Allgemein sollten lange Kabel vermieden werden!