Reale Kennlinie#
Der Verlauf einer Kennlinie hängt nicht nur von dem Hersteller des Messgerätes ab, sondern auch von äußeren Einflüssen während des Messprozesses. Genauigkeit in der Messung ist daher das Ergebnis der Wechselwirkung zwischen der Herstellung und der Anwendung eines Messsystems.
In Abb. 30 sind sowohl eine ideale als auch eine beispielhafte reale Kennlinie dargestellt. Für jede gemessene Größe gibt es eine entsprechende Messabweichung. Für jede gemessene Größe \(y\) gibt es eine spezifische Messabweichung \(A\) in Bezug auf ihren realen oder idealen Wert \(y_i\):
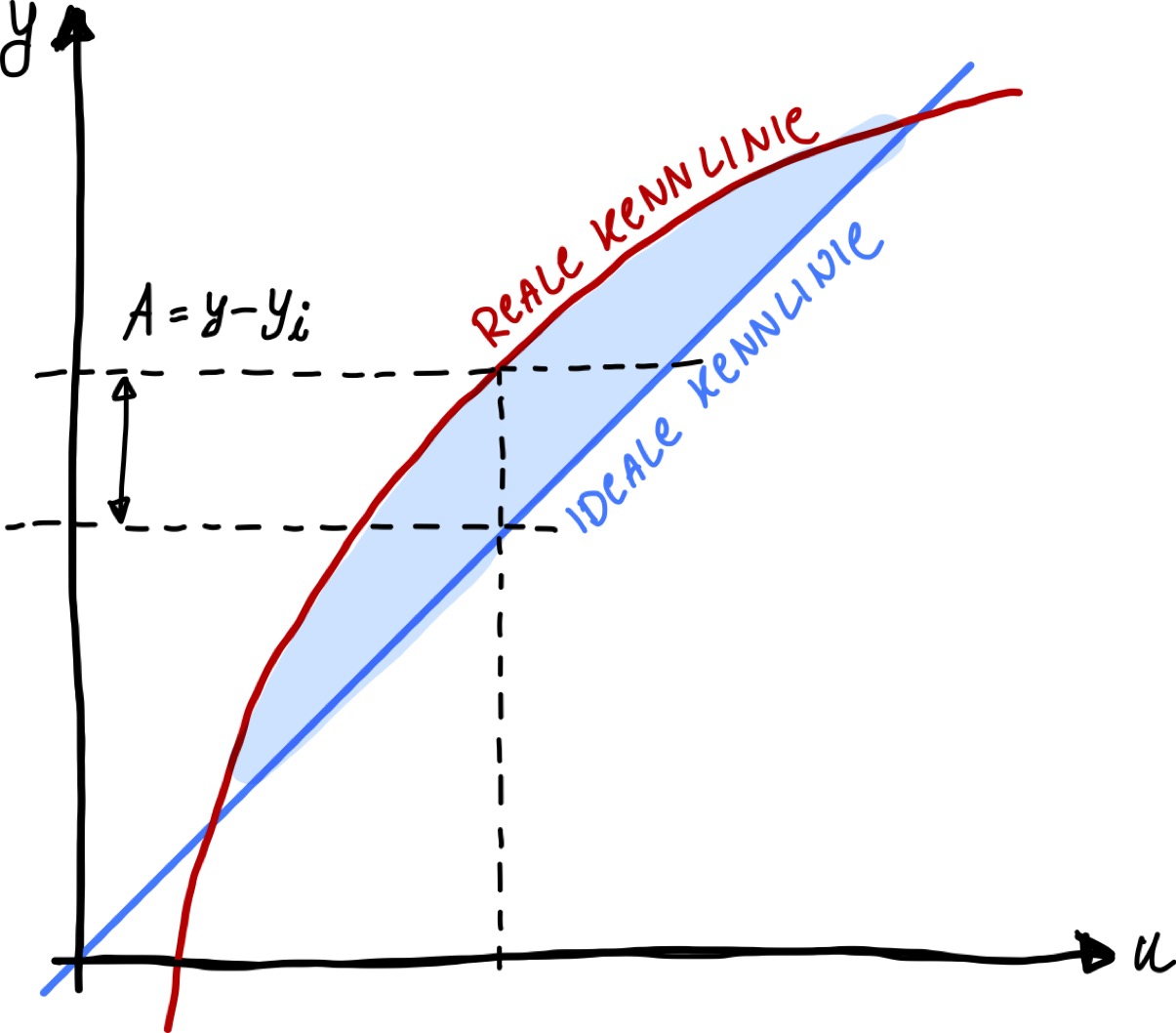
Abb. 30 Darstellung einer realen Messkennlinie.#
Die reale oder tatsächliche Kennlinie in Abb. 30 macht einen Bogen. Zwischen ihr und der idealen (linearen) Kennlinie kann die Fläche eingezeichnet werden, die ein Maß für den Linearisierungsfehler ist.
Kennlinienfehler#
Auf den grundsätzlichen Kennenlinienverlauf können durch verschiedene Einflusseffekte im Prinzip vier elementare Auswirkungen beobachtet werden. Es hängt dabei sehr stark von der konkreten Situation ab, ob ein einzelner Einflusseffekt sich primär in nur einer Art der Kennlinienabweichung zeigt oder in mehreren, d.h. es entstehen Abhängigkeiten zwischen den Komponenten. Auch wirken derartige Einflusseffekte meist auf jede einzelne Komponente eines Messsystems mit ihrer zugehörigen Einzelkennlinie. Summiert man alle diese Einflusseffekte auf alle Teilkomponenten auf, dann ergibt sich für ein konkretes Messsystem unter einer bestimmten Kombination und Anzahl von Störungen, eine ganz bestimmte reale Kennlinie.
Nach der Justierung sind alle systematischen Fehler Kennlinienfehler. Hierzu gehören Nichtlinearitäten (Abweichungen von der idealen Kennlinie) und Einfluss von Störgrößen. In Summe aller Einflüsse auf alle Teilkomponenten ergibt sich eine ganz bestimmte reale Kennlinie.
Nullpunktabweichung (Offset)#
Dieser Kennlinienfehler ist additiv. Es handelt sich daher um eine absolute Messgeräteabweichung unabhängig von der Aussteuerung einer Messeinrichtung und wird auch Offset (-fehler) genannt. An jeder Stelle des Messbereiches wird eine Abweichung mit gleichem Betrag und Vorzeichen sowohl durch systematische, als auch durch zufällige Fehlerwirkungen verursacht. Die Beschreibung der idealen Übertragungsfunktion wird durch den additiven Fehler \(A\) verändert:
wobei \(y\) das Ausgangssignal ist, was durch die Empfindlichkeit \(S\) der Kennlinie und dem Eingangssignal \(u\) bestimmt ist.
Man erkennt, dass der relative Fehler für kleine Messwerte steigt, d.h. man möchte diese Messeinrichtungen möglichst groß aussteuern.
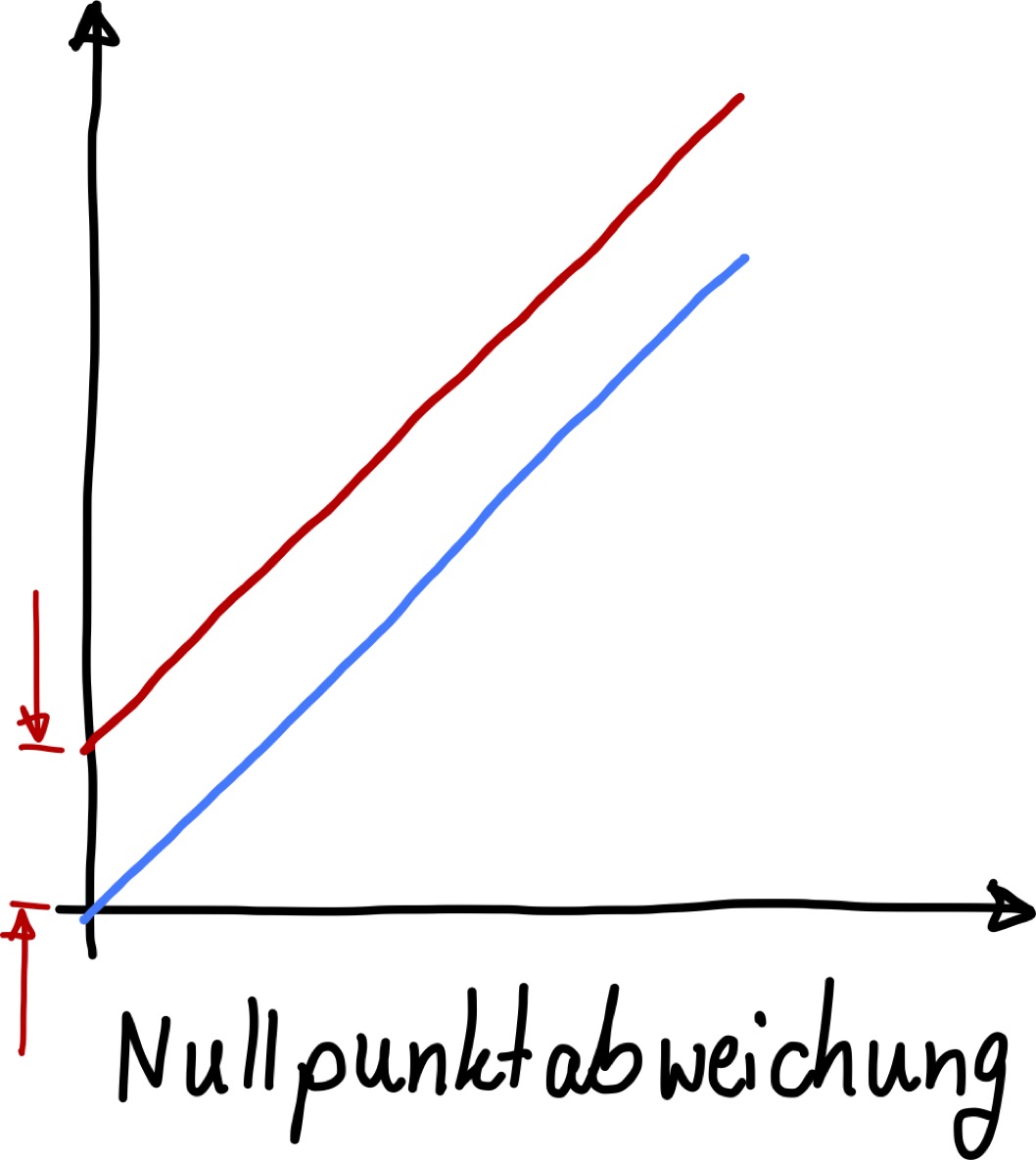
Abb. 31 Abweichung von der Idealkennlinie aufgrund eines Nullpunkt-Offsets.#
Beispiel
Angenommen man hat einen Temperatursensor. Idealerweise sollte der Sensor bei 20°C genau 20°C anzeigen und bei 25°C genau 25°C. Ein Offsetfehler sorgt dafür, dass der Messwert zu hoch oder zu niedrige ist. Statt 20°C werden 22°C und statt 25°C werden 27°C angezeigt. In diesem Fall beträgt der Offset-Fehler 2°C. Die relative Messabweichung ist bei 20°C größer (2°C/20°C = 10%) als bei 25°C (2°C/25°C = 8%).
Steigungasbweichung (Empfindlichkeitsfehler)#
Hierbei handelt es sich um eine absolute Abweichung der Anzeigegröße als Funktion ihrer Aussteuerung. Technisch wird dieser Fehlertyp auch als Verstärkungsfehler bezeichnet, d.h. man beobachtet eine unerwünschte Veränderung des Übertragungsfaktors, also die Verstärkung einer Messeinrichtung ändert sich!
Hier ist \(S_\mathrm{real}\) die reale Empfindlichkeit des Geräts, die nicht der idealen entspricht, und sowohl größer (\(S_\mathrm{real} > S\)) als auch niedriger (\(S_\mathrm{real} < S\)) als die ideale Empfindlichkeit sein kann. Auch der multiplikative Fehler kann systematische und zufällige Ursachen besitzen. Diese Art von Abweichungen verlaufen aber immer durch den Nullpunkt und sind daher eher tolerierbar, auch bei kleinen Aussteuerungen.
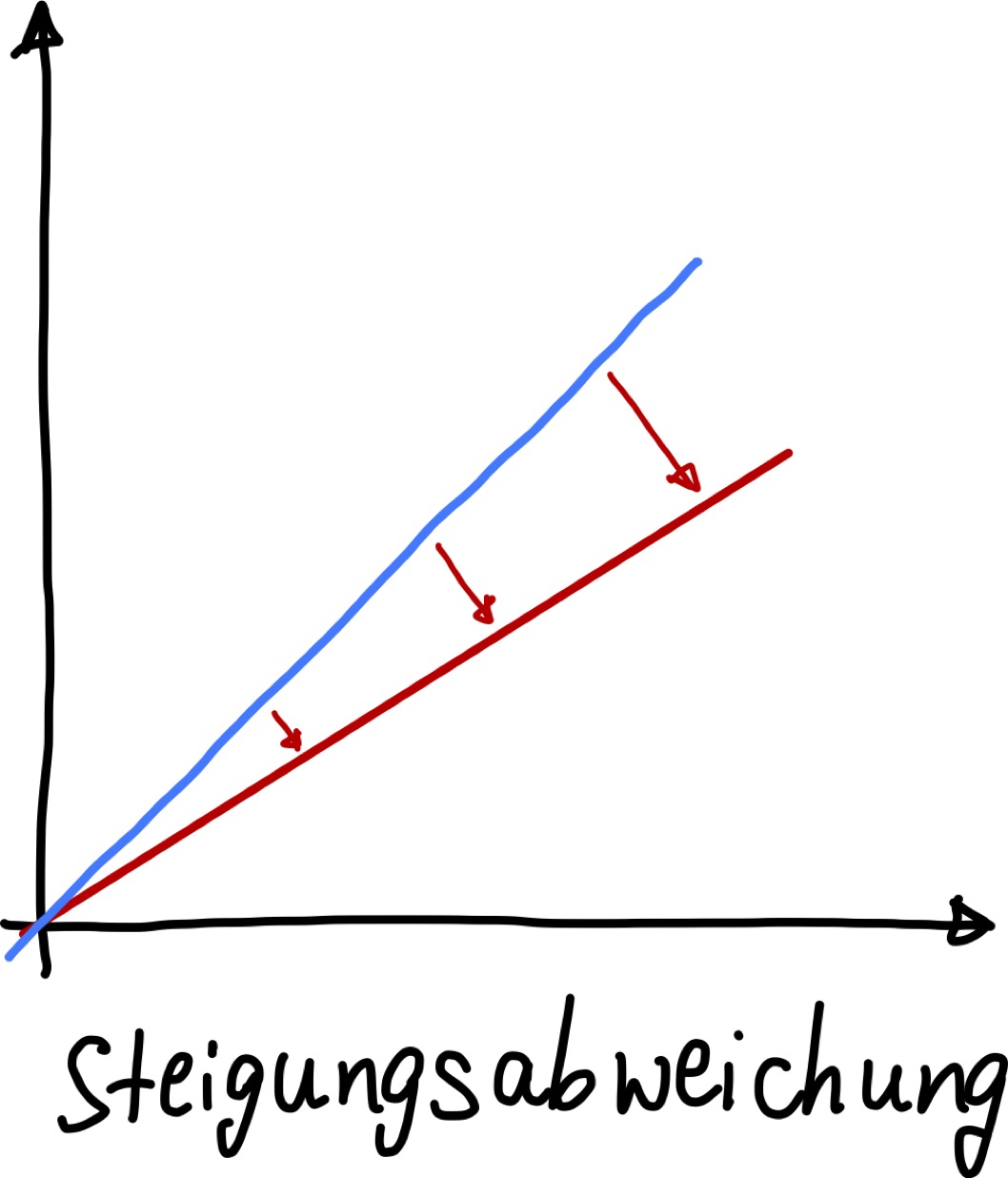
Abb. 32 Abweichung von der Idealkennlinie aufgrund einer verfälschten Steigung.#
Beispiel
Angenommen man hat einen Temperatursensor. Bei 0°C (Nullpunkt) zeigt der Sensor idealerweise und auch tatsächlich 0°C an. Bei 20°C jedoch wird aufgrund der falschen Empfindlichkeit (Steigung) ein verfälschter Messwerte angezeigt, z.B. 22°C.
Nichtlinearität#
Die oben genannten zwei Fehlertypen werden bei realen Messeinrichtungen fast immer gleichzeitig auftreten. Überlagerung der beiden Kurven führt immer zu unerwünschten Nichtlinearitäten im System.
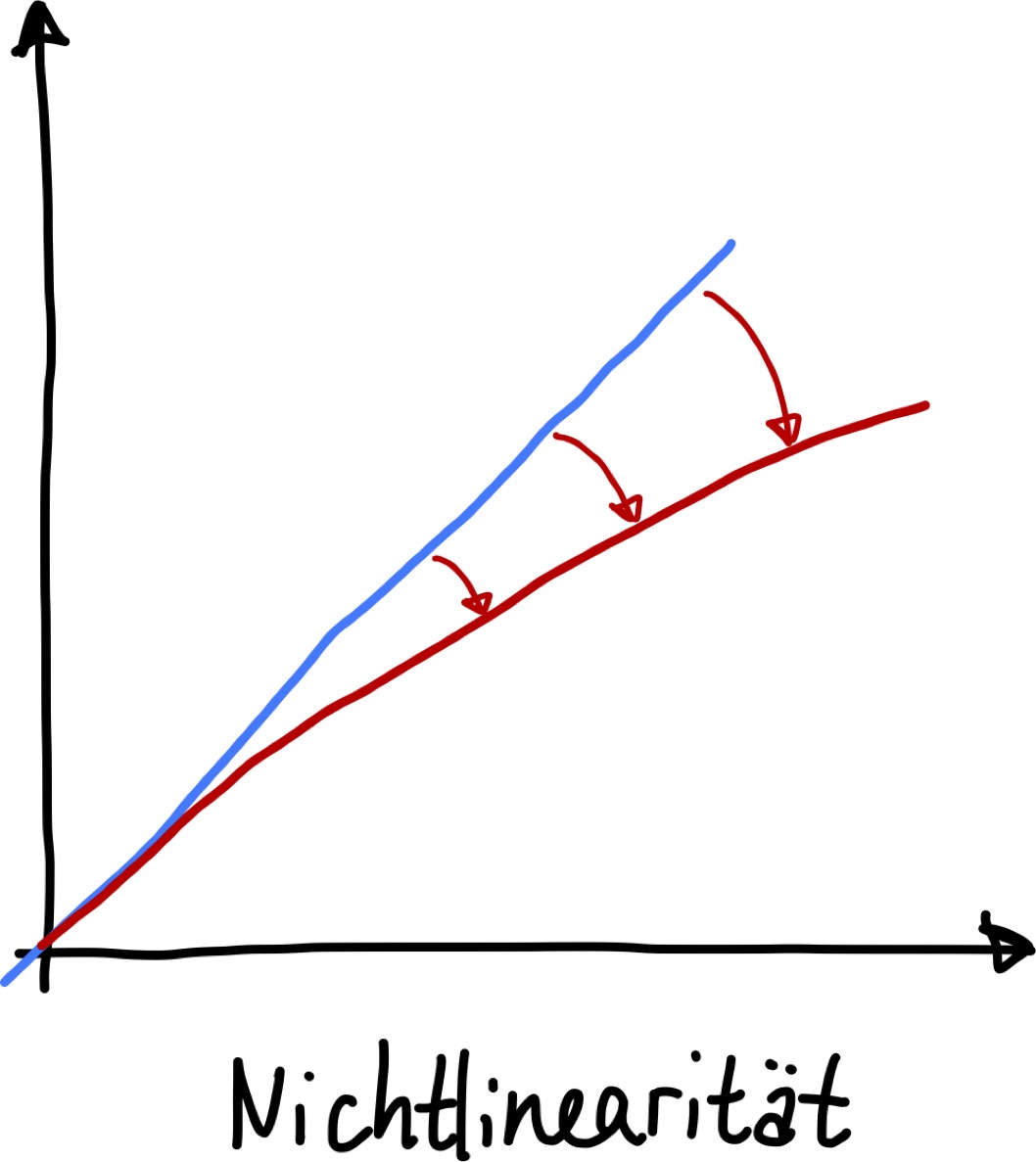
Abb. 33 Eine Kombination von Nullpunktabweichung und Steigungsabweichung führen zu Nichtlinearitäten.#
Hysterese#
Die Kennlinie unterscheidet sich, je nachdem ob die Messgröße ansteigt oder abfällt. Die Komponente hat damit gewissermaßen ein Gedächtnis. Hier sollte man sich einmal vor Augen führen, dass dies nicht bedeutet, dass das System zwei Kennlinien bestitzt. Es hat vielmehr unendlich viele Kennlinien, da die Kennlinie nicht nur von der Richtung, in die sich die Messgröße ändert, variiert, sondern sie hängt auch von der aktuellen Position der Messgröße ab.
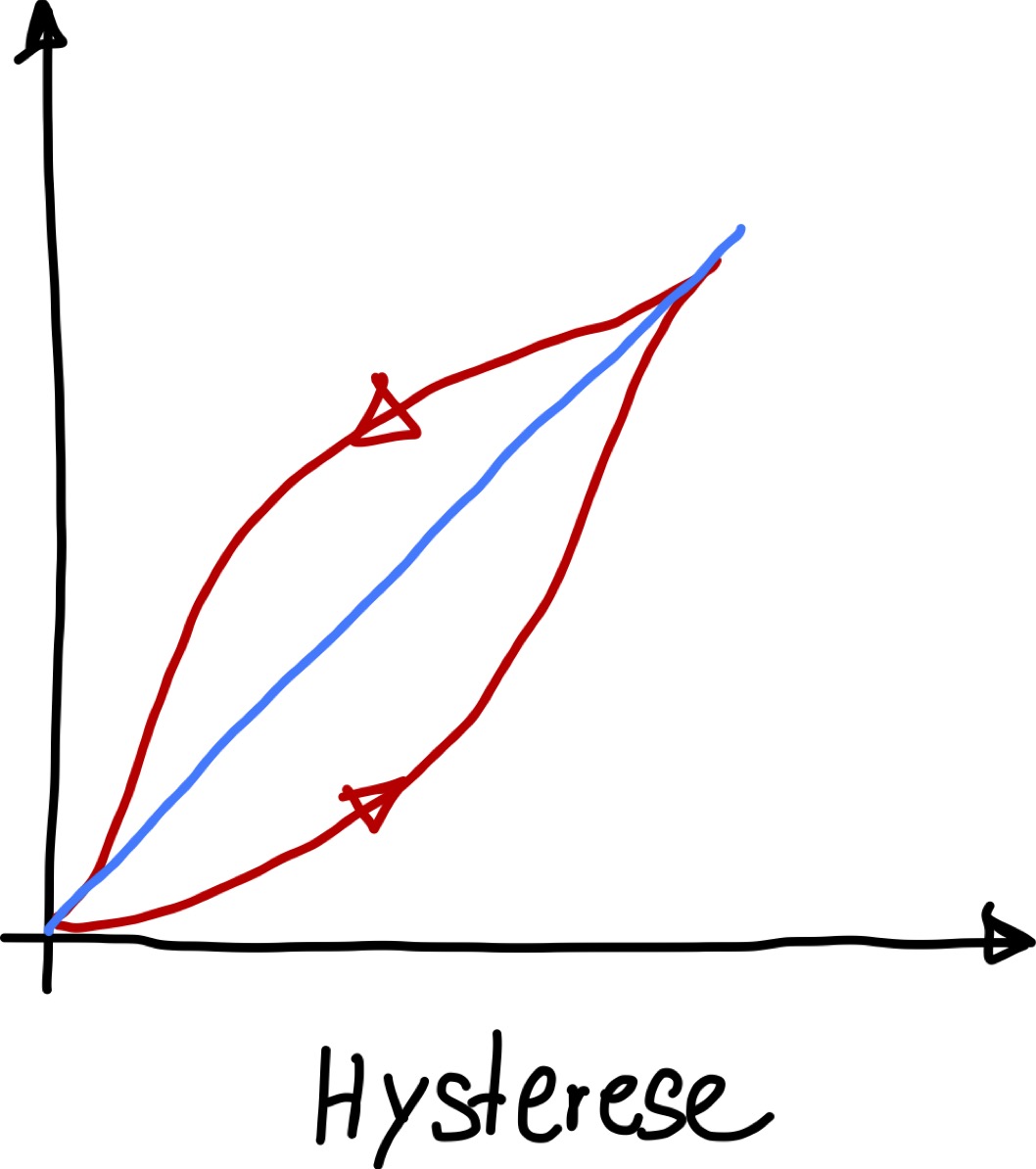
Abb. 34 Bei der Hyterese existieren unendlich viele Kennlinien, je nachdem wo man mit der Messung startet.#
Je nachdem, von welchem Umkehrpunkt aus sich die Messgröße in die jeweils andere Richtung weiter bewegt, muss man eine andere Kennlinie erwarten. Dieses Verhalten beobachtet man häuft bei mechanischen Sensorkonstruktionen (Beispiel: Druckmembran in einem Drucksensor) oder wenn magnetische Werkstoffe verbaut sind. In reinen Analogelektroniken ist die Hysterese meist nicht relevant bzw. eher relativ gering ausgeprägt.
Alle diese Kennlinienfehler…
… werden typischerweise in den Datenblättern der einzelnen Messinstrumente angegeben und müssen mitberücksichtigt werden.
Kennlinienkorrektur#
Nullpunktkorrektur#
Die Korrektur von systematischen Messabweichung erfolt über Kalibrierung von Kennlinien. Am häufigsten und am einfachsten kann eine Nullpunktkorrektur (auch Fixpunktjustierung oder Offsetkorrektur genannt) vorgenommen werden. Die Abweichung vom Nullpunkt wird hierbei korrgiert, wobei zum Zeitpunkt der Kalibrierung bestimmte Umgebungsbedingungen herrschen müssen. Störgrößen, wie Temperatur und Feuchte, müssen den allgemeinen Betriebsedingungen folgen. Was man mit dieser Nullpunktkorrektur besonders gut korrigieren kann sind Nullpunktabweichungen, die durch Streuungen im Fertigungsprozess entstanden sind.
Grundsätzlich gilt, dass eine Referenz benötigt, entweder in Form einer definierten Messgröße, oder in Form eines Referenz-Messgeräts, welches seinerseits vorher kalibriert wurde. Bei der Erstinbetriebnahme an einem Kalibrierpunkt wird einmalig also beispielsweise eine wohlbekannte Messgröße angelegt. Das Messgerät wird nun mit einem Messwert antworten, der von der aktuell herrschenden realen Kennlinie bestimmt wird. Er wird vermutlich leicht über oder unter der idealen (gestrichelten) Kennlinie verschoben sein. Im nachfolgenden Bild ist der Kalibrierpunkt am Nullpunkt des Messbereichs. Für viele Messgeräte ist der Nullpunkt ein geeigneter Kalibrierpunkt, Beispiele sind:
Wägesystem: hier wird schlichtweg einfach kein Wägegut aufgebracht. Auch Leergewichte von Wägebehältern können so wegkalibriert werden.
Abstandsmessungen: ein Abstand von Null ist meist relativ einfach einstellbar
elektrische Größen: auch bei Spannung, Strom oder Widerstand ist die Nullpunktkalibrierung einfach realisierbar.
Beschleunigungssensoren: diese werden typischerweise parallel zur Erdoberfläche auf einer Ebene gelagert, sodass nicht einmal die Erdbeschleunigung auf diesen Sensor wirkt
Temperaturmessungen: hier ist es tatsächlich schwierig. Für 0°C müssten gefrierendes Wasser oder eine Klimakammer genutzt werden. Wurde die Nullpunktabweichung einmal bestimmt, müssen alle nachfolgenden Messungen vorzeichenrichtig korrigiert werden. Fällt die Nullpunktabweichung positiv aus (es wird immer ein zu hoher Messwert ausgegeben), muss der Betrag später vom Messwert abgezogen werden. In der Regel verfügt das Messgerät über eine eingebaute Funktion, sodass die Kalibrierung nicht in der Nachverarbeitung berücksichtigt werden muss. Sollten sich Betriebsbedingungen ändern, ist eine Rekalibrierung nötig.
Fixpunktjustierung oder auch Offsetkorrektur genannt
Nach der Fixpunktjustierung geht die Kennlinie durch den Anfangspunkt und durch den Endpunkt.
Der Messbereich wird auf den Anzeigebereich abgebildet.
Im Messanfang und Messende ist damit der Fehler null.
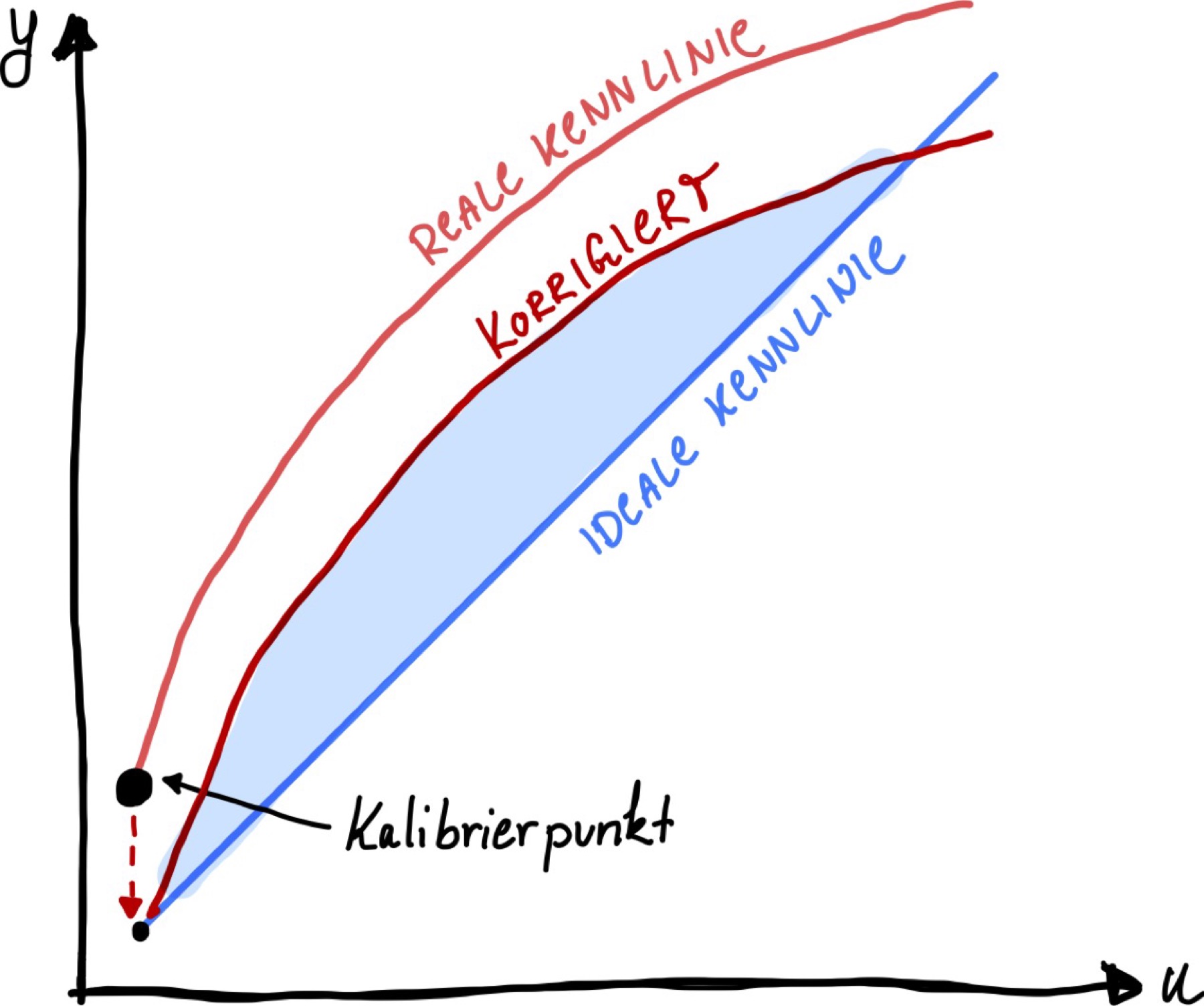
Abb. 35 Offset-Korrektur einer realen Kennlinie.#
Toleranzbandjustierung#
Eine Erweiterung der Nullpunktkorrekt ist die Toleranzbandjustierung, die den Fehler um einen Faktor 2 gegenüber der Nullpunktkorrektur reduziert, indem die Kennlinie einfach noch weiter additiv verschoben wird. Trotz der Fehlerreduktion hat die Methode den Nachteil, dass die Kennlinie nicht mehr durch den Nullpunkt geht.
Die Toleranzbandjustierung entsteht durch eine zusätzliche additive Verschiebung der Fixpunktjustierung.
Ziel ist es, den maximalen Fehler im Messbereich möglichst klein zu gestalten.
Der maximale Fehler wird im Vergleich zur Fixpunktjustierung auf die Hälfte reduziert.
Kennlinie geht allerdings nicht mehr zwangsläufig durch Anfangs- und den Endpunkt.
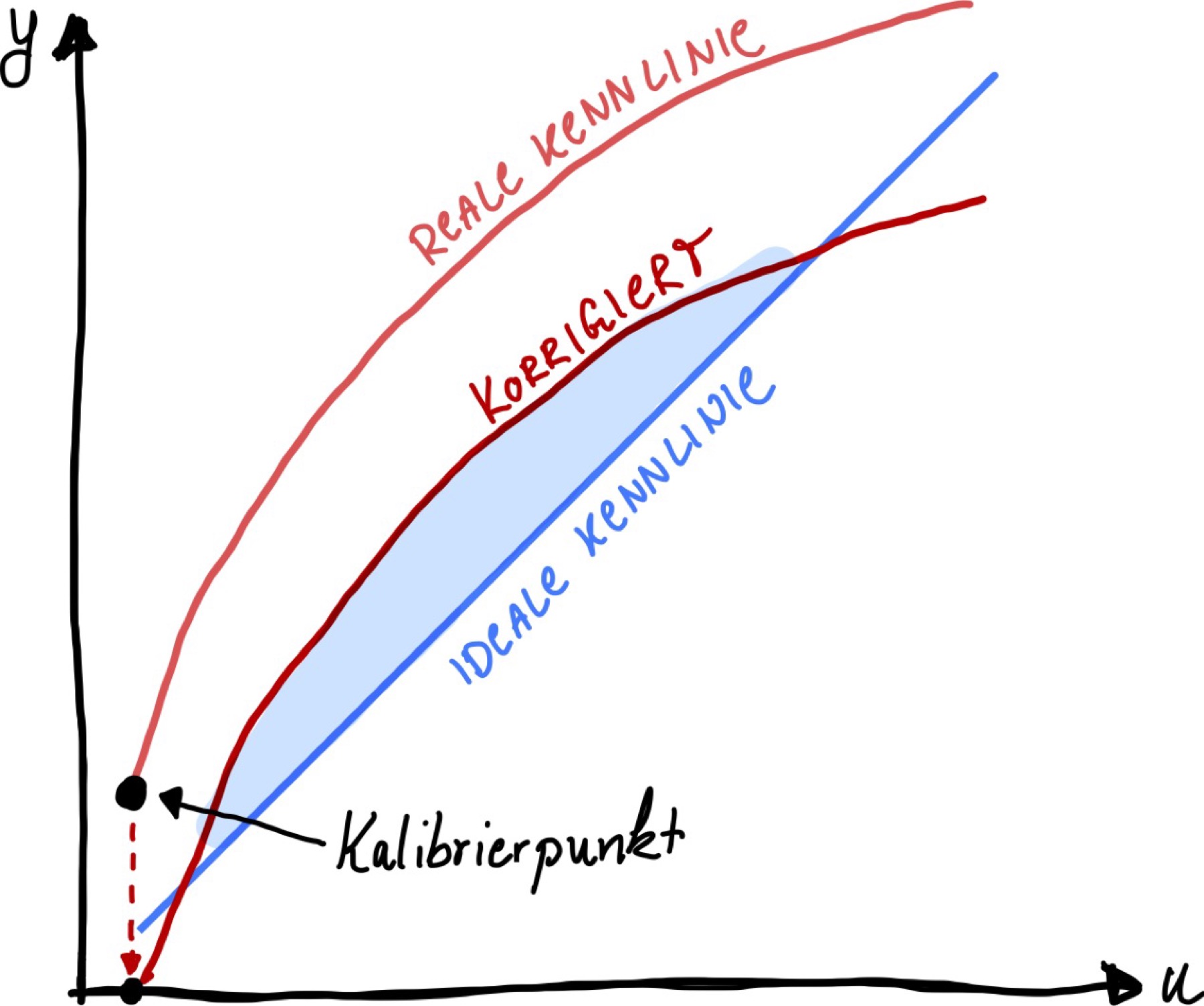
Abb. 36 Toleranzband-Justierung einer realen Kennlinie.#
Steigungskorrektur#
Die Nullpunktkorrektur kann auch mit einer sogenannten Steigungskorrektur vorgenommen werden, wie es im nachfolgenden Bild dargestellt ist. Für die Steigungskorrektur sind zwei Kalibriermessungen notwendig, d.h. es werden zwei Datenpunkte benötigt. Häufig ist der eine Datenpunkt der Messwert der Nullpunktkalibrierung. Der zweite Datenpunkt sollte möglichst nah am Messbereichsendwert liegen, sodass eine große Spanne abgedeckt wird. Die reale Kennlinie wird nun wieder unter Betriebsbedingungen in zwei Schritten korrigiert: Sie wird einerseits vertikal verschoben und zusätzlich um ihren Nullpunkt gedreht, sodass in beiden Kalibrierpunkten keine Messabweichung mehr besteht (siehe Bild). Anschaulich kann man sich Hilfsgeraden durch die Kalibrierpunkte vorstellen. Die Steigung einer Hilfsgerade durch die Kalibrierpunkte weicht von der Steigung der idealen Kennlinie ab (im Bild ist sie steiler). Mittels Korrektur werden die beiden Steigungen einander angepasst.
Am ersten Kalibrierpunkt, dem Nullpunkt \(u_0 = 0\) wird folgender Wert gemessen:
Dann beträgt die Messabweichung an diesem Punkt:
Bei einer einfachen Nullpunktkorrektur müsste die reale Kennlinie folglich um diesen Wert verschoben werden, damit am Nullpunkt die Abweichung verschwindet. Am zweiten Kalibrierpunkt, an der Stelle \(u_1\), gilt das Gleiche. Wir messen den folgenden Wert:
und berechnen die Messabweichung, bzw. den Korrekturwert, wie folgt, wobei wir den richtigen Wert \(y_r\) an der Stelle miteinbeziehen:
Dieser Wert müsste also von allen nachfolgenden Messungen abgezogen werden. Für alle Messwerte dazwischen, ändert sich die Messabweichung linear. Wir berechnen also eine Gerade durch die beiden Kalibrierpunkte und können alle anderen Messabweichungen interpolieren:
Die Nullpunkt- und Steigungskorrektur ist sehr aufwendig: Es werden zwei Kalibriermessungen benötigt.
Zweiter Kalibrierpunkt ist meist der Messbereichsendwert (MBE), da hier die größte Spanne erreicht wird.
Die reale Kennlinie geht durch Nullpunkt und wird anschließend noch rotiert
Korrigierte Kennlinie hat eine kleinere Steigung und ist somit weniger empfindlich!
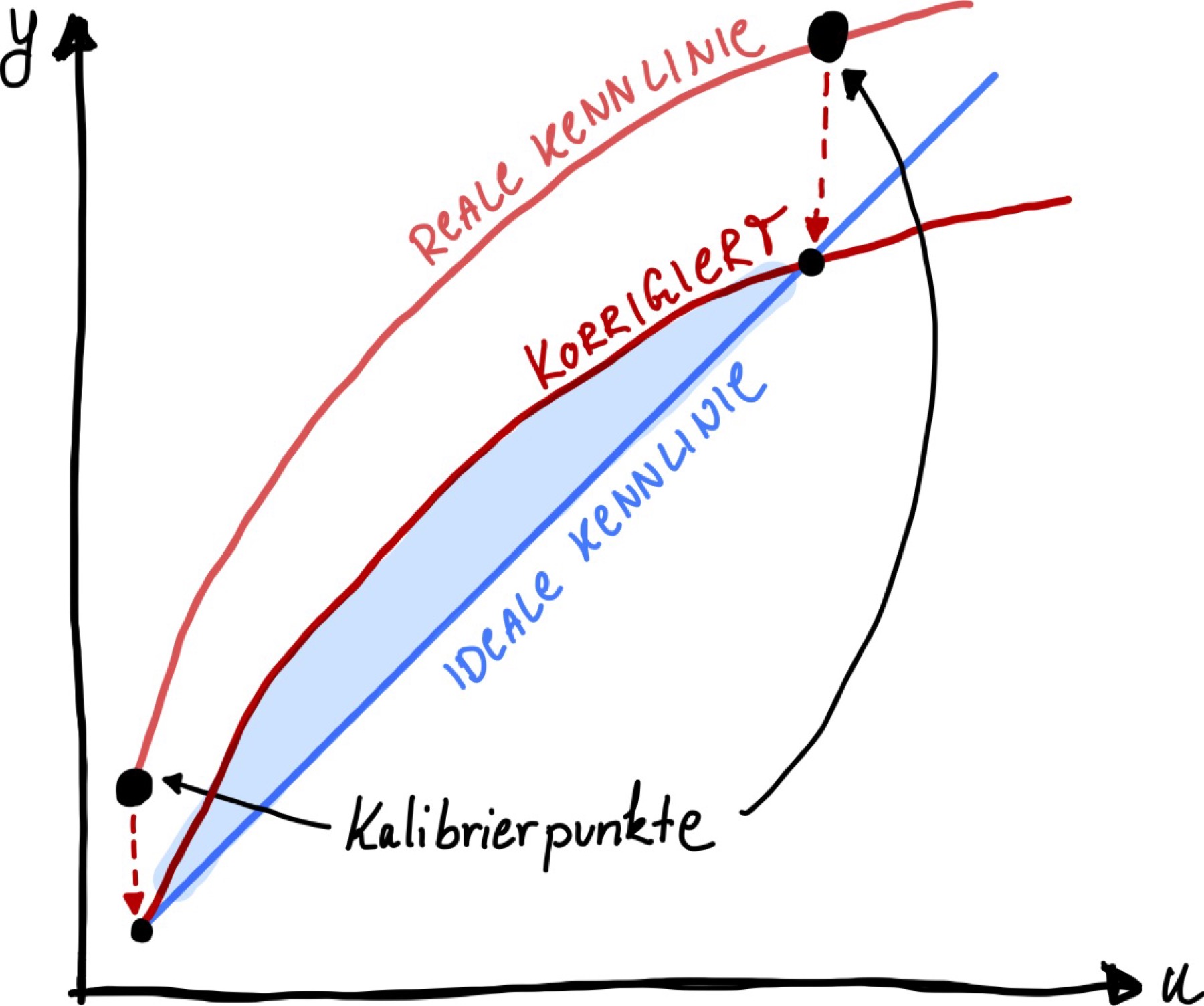
Abb. 37 Offset und Steigungskorrektur einer realen Kennlinie.#
Digitalisierung#
Im Zuge der Digitalisierung wird der unendliche Wertebereich einer analogen Größe, wie z.B. einer elektrischen Spannung, auf einen endlichen, diskreten Wertebereich abgebildet:
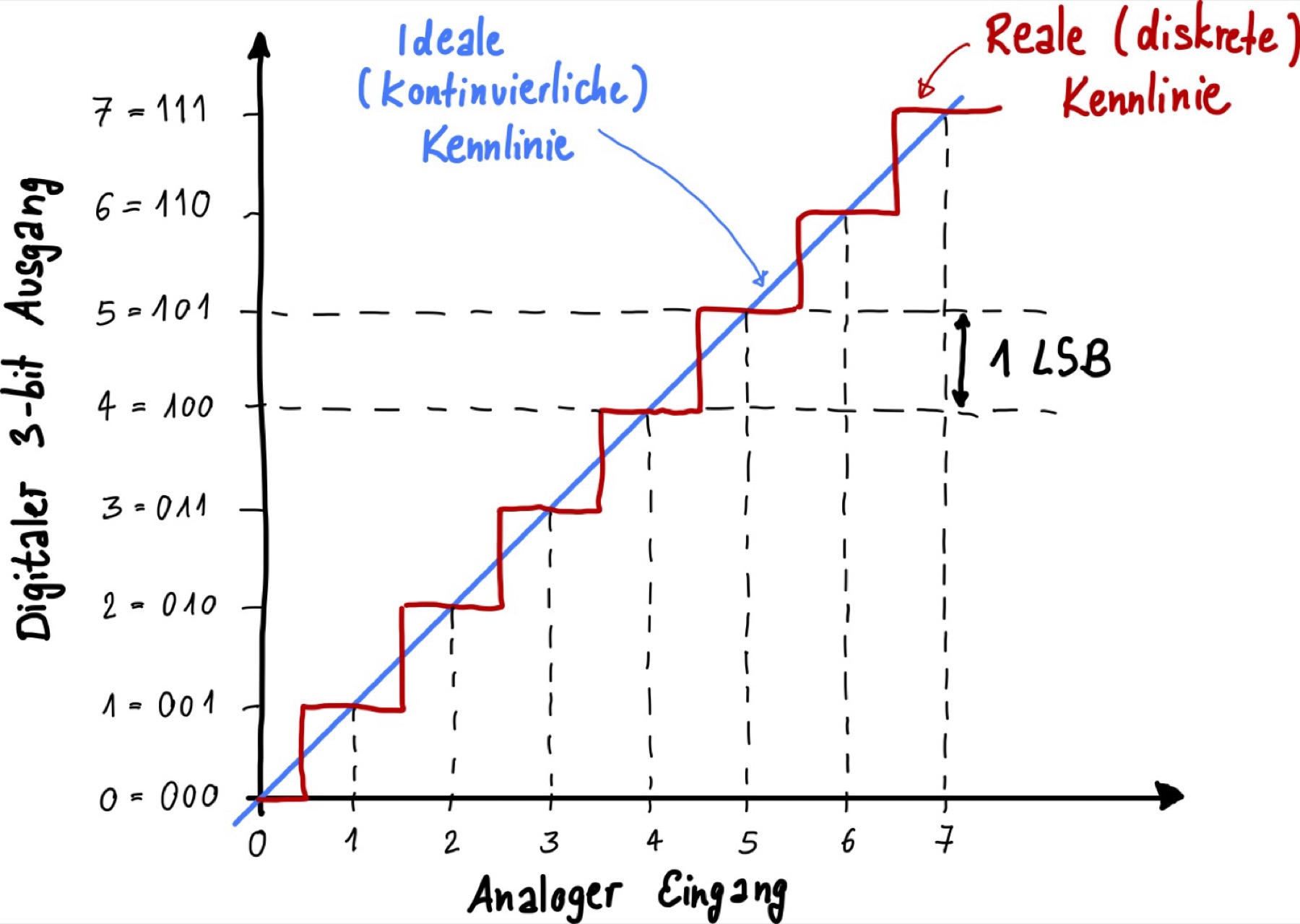
Die kontinuierliche analoge Spannung wird in viele kleine Stufen unterteilt. Die gestufte (Treppen-)Kurve in der obigen Abbildung zeigt die reale Übertragungskurve eines 3-Bit-Analog-Digital-Umsetzers (ADU). Das digitale Ausgangssignal bleibt konstant bei einem festen Wert, solange sich das analoge Eingangssignal innerhalb eines Inkrements, also 1 LSB (least significant bit), verändert. Wenn sich das Eingangssignal nur minimal ändert, z.B. von 1,1V auf 1,9V, ändert sich der digitale Ausgangswert nicht und bleibt konstant auf 001.
Auflösung#
Es ist offensichtlich, dass bei der Digitalisierung Informationen verloren gehen. Die analogen Spannungswerte sind beliebig genau und haben unendlich viele Nachkommastellen, werden jedoch nur auf einen begrenzten, diskreten Wertebereich mit einer begrenzten Anzahl von Stufen projiziert. Je feiner diese Stufen sind (also je mehr Bits verwendet werden), desto besser ist die Auflösung. Erst wenn ein Grenzwert überschritten wird, wird die nächste Stufe erreicht, und der Computer zeigt einen neuen Spannungswert an. Die Zwischenschritte werden jedoch nicht angezeigt.
Es ist wichtig zu beachten, dass es in der Praxis nicht möglich oder sinnvoll ist, eine beliebig hohe Auflösung zu verwenden. Der technische Aufwand steigt mit der Anzahl der Bits erheblich an. Daher ist es wichtig, vor der Messaufgabe zu überlegen, welche Auflösung benötigt wird, insbesondere wenn die Auflösung durch andere Parameter begrenzt ist, wie z.B. die Genauigkeit der Referenzmessung und Kalibrierung.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML
from matplotlib.widgets import Slider
plt.rcParams['font.size'] = 13; # Schriftgröße
# Initialize the figure and axis
fig, ax = plt.subplots(figsize=(7, 4))
f = 1
# Create a function to update the plot for each frame of the animation
def animate(bit):
ax.clear() # Clear the previous frame
# Set the signal frequency and time axis
t = np.linspace(0, 1, 150)
# Generate the analog signal
analoges_signal = np.sin(2 * np.pi * f * t)
# Digitalisierung des analogen Signals
quantisierungs_bits = bit # Anzahl der Quantisierungsbits
digitalisiertes_signal = np.round(analoges_signal * (2**(bit-1)))
max_amplitude = 2**(bit-1) # Maximaler Amplitudenwert
digitalisiertes_signal = digitalisiertes_signal / max_amplitude
# Initialisierung des Plots
ax.plot(t, analoges_signal, label='Analoges Signal', alpha=0.3, lw = '3')
ax.stem(t, digitalisiertes_signal, 'tab:red', markerfmt='ro', basefmt=" ", linefmt='r-', label = '%d Bit Digitalwandler'%(bit))
# Set plot labels and legend
#ax.set_title('Analog zeitdiskret: Abgetastete Sinuswelle')
ax.set_xlabel('Zeit (s)')
ax.set_ylabel('Amplitude')
ax.set_xlim([0, 1])
ax.set_ylim([-1.1, 1.1])
ax.grid(True)
ax.legend(loc='upper right')
# Create an animation by varying fs from 1 to 10 with a step of 1
ani = FuncAnimation(fig, animate, frames=range(1, 17), repeat=False)
ani.save('digital_bit.mp4', writer='ffmpeg', dpi=300)
# Display the animation
plt.tight_layout()
plt.close()
HTML(ani.to_jshtml())
Quantisierungsabweichung#
Dadurch dass der Wertebereich begrenzt ist, ergeben sich absolute Messabweichungen beim Digitalisierungsprozess. Dies wird auch absoluter Digitalisierungsfehler genannt. Aus der Kennlinie kann man diesen Fehler ablesen, er ergibt sich aus dem Digitalwert und dem idealisierten Kennlinienwert. Im worst case beträgt die maximale Abweichung:
Die relative Messabweichung bezogen auf den Wertebereich ist dadurch:
Für einen A-D-Wandler mit einer Auflösung von 10 Bit ist die relative Abweichung infolge der Quantisierung anzugeben:
Show code cell source
n_bits = 10
print('rel. Abweichung: \t\t\t', 1/(2**n_bits-1)*100, '%')
print('rel. Abweichung (Näherungsformel): \t', 1/2**n_bits*100, '%')
rel. Abweichung: 0.09775171065493646 %
rel. Abweichung (Näherungsformel): 0.09765625 %
Mehr zur Digitalisierung kommt noch mal später in der Vorlesung.
Gesamtkennlinie#
Nachdem wir uns einige Beispiele von Kennlinien, also Empfindlichkeitskurven, angesehen haben, können wir diese natürlich auch hintereinander schalten. Dies ist insbesondere wichtig, da Messsysteme eigentlich immer aus mehreren Komponenten bestehen, wie wir am Anfang des Kapitels in der Grundstruktur bereits gesehen haben. Wie in Abb. 38 dargestellt, hat jede einzelne Komponenten ihre eigene Kennlinie und wandelt eine Eingangsgröße in eine Ausgangsgröße um. Diese Kennlinien werden nun hintereinander geschaltet, sodass daraus eine Kennlinie resultiert, die das gesamte Messsystem beschreibt. Die einzelnen Kennlinien werden hierfür einfach aneinander multipliziert.
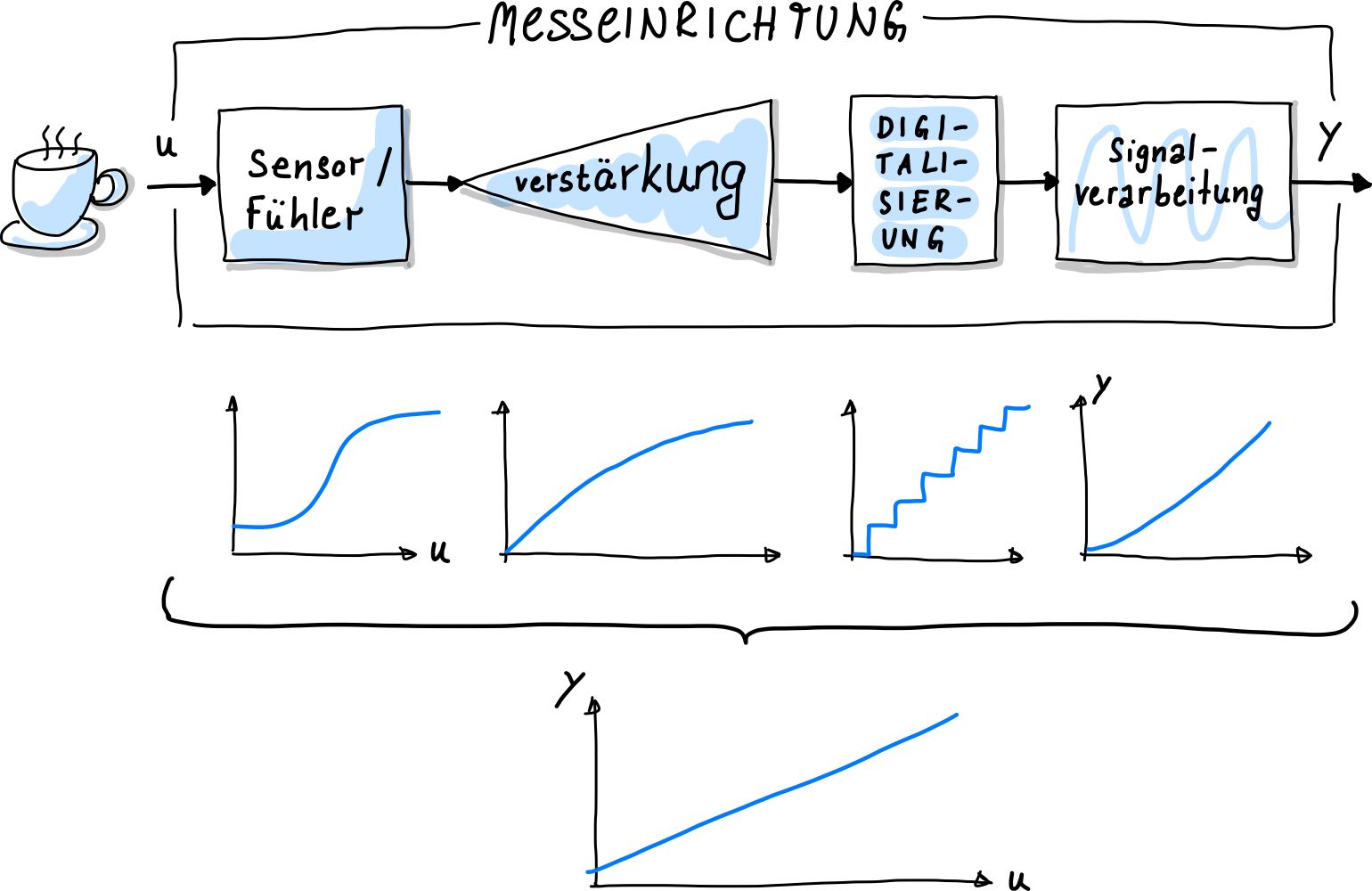
Abb. 38 Gesamtkennlinie eines Messsystems ergibt sich aus der Muliplikation der Einzelkennlinien#
Optimalerweise möchte man erreichen, dass die Gesamtkennlinie eines System über einen möglichst großen Eingangsbereich für \(u\) linear ist, d.h. dass die einer Geraden entspricht. Dafür müssen die individuellen Kennlinien der Komponenten nicht zwangsläufig alle linear sein, sondern können sich am Ende kompensieren. Dies ist die große Kunst des Herstellens von Messsystemen.
Nun hängt allerdings der Verlauf einer Kennlinie nicht nur von der Herstellung ab, sondern auch von (äußeren) Einflusseffekten während des Messprozesses. Es hängt folglich immer von der Herstellung und Anwendung eines Messsystems ab, wie genau man wirklich messen kann.
Aufgabe
Versuche im nächsten Code-Block eine ideale Gesamtkennlinienfunktion in einem bestimmten Bereich zu erhalten, ohne dass alle einzelnen Kennlinien linear sind. Verändere hierfür die Funktionen f1, f2, f3 und deren Parameter a_i, b_i, c_i
.
Show code cell source
#Benötigte Libraries:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
import seaborn as sns
import time
import warnings
warnings.filterwarnings('ignore')
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
def f1(x):
a_1 = .0
b_1 = 1.0
return b_1 * x + a_1
def f2(x):
a_2 = 0.0
b_2 = 1.0
c_2 = 1.0
return c_2 * x**2 + b_2 * x + a_2
def f3(x):
a_3 = 1.0
b_3 = 1.0
return b_3 * x + a_3
start = 0.0
stop = 10.0
u = np.linspace(start, stop, num=50)
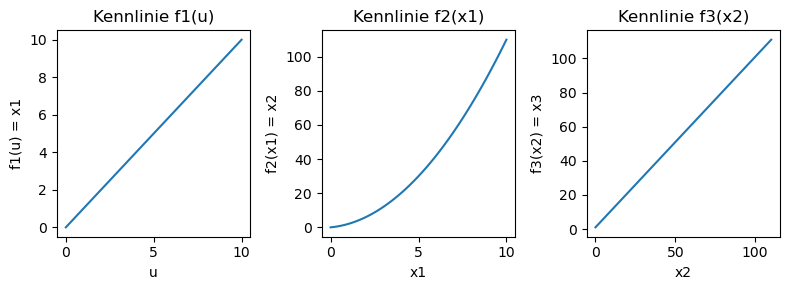
## Hintereinanderschaltung:
x1 = f1(u)
x2 = f2(x1)
x3 = f3(x2)
f, axs = plt.subplots(1,3,figsize=(8,3))
axs[0].plot(u, x1)
axs[0].set_xlabel('u')
axs[0].set_ylabel('f1(u) = x1')
axs[0].set_title('Kennlinie f1(u)')
axs[1].plot(x1, x2)
axs[1].set_xlabel('x1')
axs[1].set_ylabel('f2(x1) = x2')
axs[1].set_title('Kennlinie f2(x1)')
axs[2].plot(x2, x3)
axs[2].set_xlabel('x2')
axs[2].set_ylabel('f3(x2) = x3')
axs[2].set_title('Kennlinie f3(x2)')
plt.tight_layout()
plt.show()
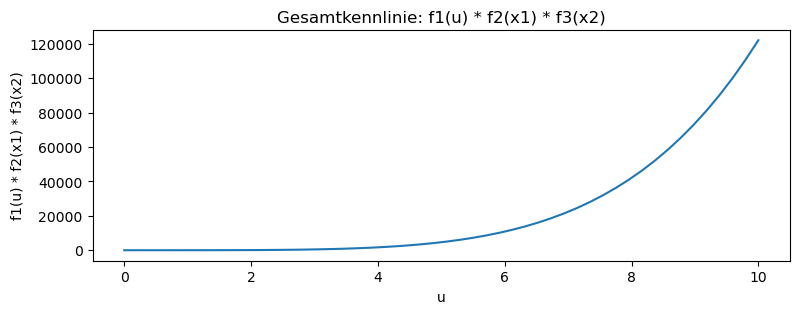
## Gesamtkennlinie:
f, axs = plt.subplots(1,1,figsize=(9,3))
axs.plot(u, x1*x2*x3)
axs.set_xlabel('u')
axs.set_ylabel('f1(u) * f2(x1) * f3(x2)')
axs.set_title('Gesamtkennlinie: f1(u) * f2(x1) * f3(x2)')
plt.show()
Messketten-Empfindlichkeit und Auflösung#
Die wichtigste Kenngröße, die Empfindlichkeit der Messkette, kann analog einfach über Multiplikation berechnet werden. Das folgende Beispiel, in Abb. 39 dargestellt, zeigt, wie eine Temperatur über die Umwandlung in zuerst eine Spannung und dann in Stromstärke am Ende in eine analoge Anzeige gewandelt wird. Die Messketten-Empfindlichkeit ist
wobei \(n\) die Anzahl der Messglieder ist. Im Beispiel in Abb. 39 bewegt sich der Zeiger um 10 Skaleneinheiten weiter, wenn sich die Temperatur um 1°C verändert. Die Auflösung des Messsystems, also 0,5 Skaleneinheiten (was man typischerweise per Auge noch ablesen könnte) beträgt somit 0,05°C = 50mK.

Abb. 39 Beispiel für die kombinierte Empfindlichkeit einer Messkette.#
Optimale Kennlinien#
Messbereich herabsetzen#
Ziel ist es, eine möglichst optimale Kennlinie zu erhalten, welche einer Geraden entspricht. Dadurch entstehen auch die wenigsten Kennenlinienfehler. Am Beispiel des Dehnungsmessstreifens (DMSs) soll dies einmal erläutert werden. Dehnungsmessstreifen (DMS; englisch strain gauge) sind Messeinrichtungen zur Erfassung von dehnenden und stauchenden Verformungen. Sie ändern schon bei geringen Verformungen ihren elektrischen Widerstand und werden als Dehnungssensoren eingesetzt. Hierbei wird ein Draht in einer Meanderstruktur hin- und zurück gelegt und gibt je nach seiner Länge einen anderen Widerstandswert aus.
Ein DMS ist nur für kleine Dehnungen linear, das heißt er zeigt ein stark nicht-lineares Verhalten wenn sich seine relative Länge um mehr als 0,1% ändert. Die Idee ist nun, den DMS ausschließlich in diesem Bereich zu benutzen. Dafür wird eine weitere Komponente in der Messkette benötigt, die die an den DMS angelegte Eingsangsgröße auf einem bestimmten Bereich limitiert. Sollen auch größere Auslenkungen als 1 mm gemessen werden, so wird diese Komponente außerdem dafür sorgen, dass eine Verminderung der Auslenkung statt findet. Dies kann beispielsweise über eine Blattfeder realisiert werden. Diese nimmt große Auslenkungen auf und projiziert sie auf kleine Auslenkungen (in Abb. 40 verkörpert durch eine Komponenten mit Empfindlichkeit \(S_0\) << 1), die dann mittels DMS gemessen werden können. Damit die Messgröße unverändert bleibt, dürfen wir am Ende die Verstärkung (\(S_1\) >> 1) nicht vergessen, sodass \(S_0 \cdot S_1 = 1\). Dies nennt man auch Kompensations-Bedingung.
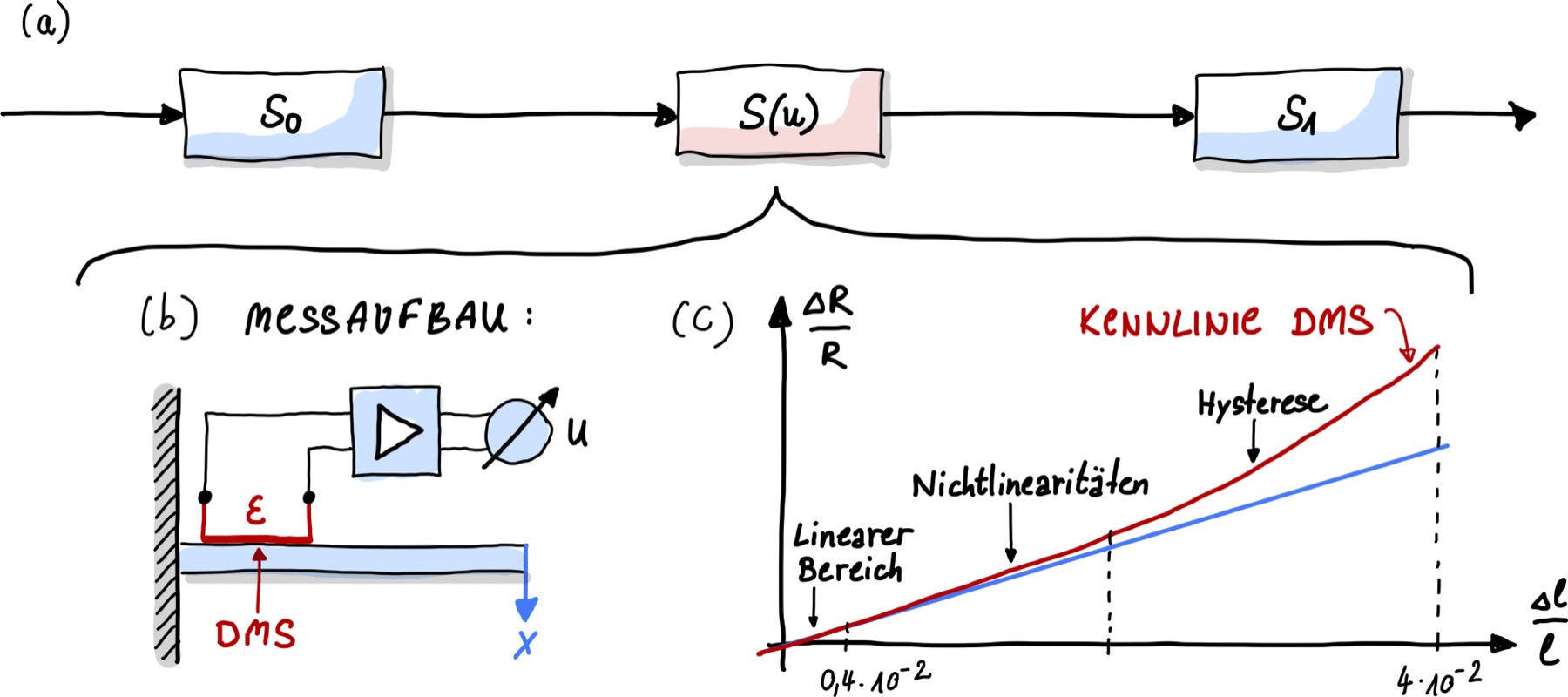
Abb. 40 Beispiel für das Herabsetzen des Messbereichs. Die Messung mit einem Dehnungsmessstreifen (DMS) ist nur für kleine relative Längenänderungen \(\Delta l / l\) linear. Zusätzliche Komponenten, \(S_1, S_2\), in der Messkette können so gewählt werden, dass auch größere Änderungen in \(x\) messbar werden, z.B. indem der DMS an eine Blattfeder angebracht wird, der die Messgröße \(x\) aufnimmt und in eine Änderung \(\varepsilon\) überführt. Eine Verstärker-Stufe sorgt für die Kompensation, sodass \(S_0 \cdot S_1 = 1\) gilt.#
Ein detaillierte Herleitung für die Kompensationgsbedingung ist im Punte Leon Kapitel 3 zu finden.
Zwei nicht-lineare Komponenten hintereinander schalten#
Angenommen, man habe zwei nicht-lineare Komponenten in einem Messsystem, die hintereinander geschaltet werden (in Reihe). Die Komponenten haben jeweils die Empfindlichkeiten \(S_1(u_1)\) und \(S_2(u_2)\), wobei \(u_1\) und \(u_2\) die jeweiligen Eingangssignale der Komponente sind.

Abb. 41 Reihenschaltung zweier Komponenten mit nicht-linearem Übertragungsverhalten.#
Die Gesamt-Empfindlichkeit lässt sich über das Produkt der Einzel-Empfindlichkeiten berechnen und es folgt:
Möchte man nun eine lineare Gesamtkennlinie erhalten, so muss gelten
Formal erhält man eine exakte Lösung die obigen Bedingung, wenn die eine Kennlinie \(f_2\) genau der Umkehrfunktion der ersten Kennlinie entspricht, \(f_1^{-1}\). Für den allgemein Fall, kann man die Bedingung in Abhängigkeit von \(u_1\) wird als eine Taylor-Reihe um den Arbeitspunkt herum entwickeln. Höhere Ordnungen der Taylor-Reihenentwicklung (2., 3., … Ableitungen) werden gleich Null gesetzt. Hat man jedoch höhere Ansprüche, was die Linearisierung betrifft, so müssen diese in der Taylor-Entwicklung miteinbezogen werden.
Es folgt die allgemeine Linearitätsbedingung
Beispiele sind wieder im Punte Leon zu finden.
Messbereich klever auswählen#
Stehen mehrere Kennlinien zur Verfügung bietet es sich an, einen gewünschten kleinen Messbereich auszuwählen, nämlich dort, wo die Kennlinie möglichst linear ist und eine hohe Empfindlichkeit aufweist. Wenn man besonders hohe Ansprüche hat bietet es sich auch an, die Empfindlichkeit gegenüber der Eingangsgröße aufzutragen, und nicht nur die Kennlinie. Dort, wo die Empfindlichkeit möglichst hohe Werte annimmt und möglichst flach ist, hat man den optimalen Arbeitspunkt des Messgerätes gefunden.
Tatäschlich kann man sich dies auch mathematisch herleiten, indem wieder ein Gütemaß definiert wird, was die quadratischen Abweichungen der Empfindlichkeit von der mittleren Empfindlichkeit über den gewünschten Messbereich integriert. Das Gütemaß soll möglichst minimal sein, d.h. die Ableitung soll Null werden, und so kann man für verschiedene Messbereiche die maximale Abweichung zur idealen (hier mittleren) Empfindlichkeit analytisch berechnen und optimieren!
Differentielle Methode#
Bei zwei gleichartigen Teilsystemen, welche mittels einer Parallelschaltung zusammengeschlossen werden, kann über Gleichtaktunterdrückung auch die Kennlinie linearisiert und zugleich eine Steigerung der Empfindlichkeit erreicht werden (ähnlich wie die differentielle Signalübertragung, wo sich gemeinsame Fehlerquellen aufheben können). Die Teilsysteme, oder z.B. gleichartige Sensoren, sind so angeordner, dass Abweichungen gegensinnig wirken. Dies ist nur für systematische Abweichungen möglich, wo das Vorzeichen bekannt ist.
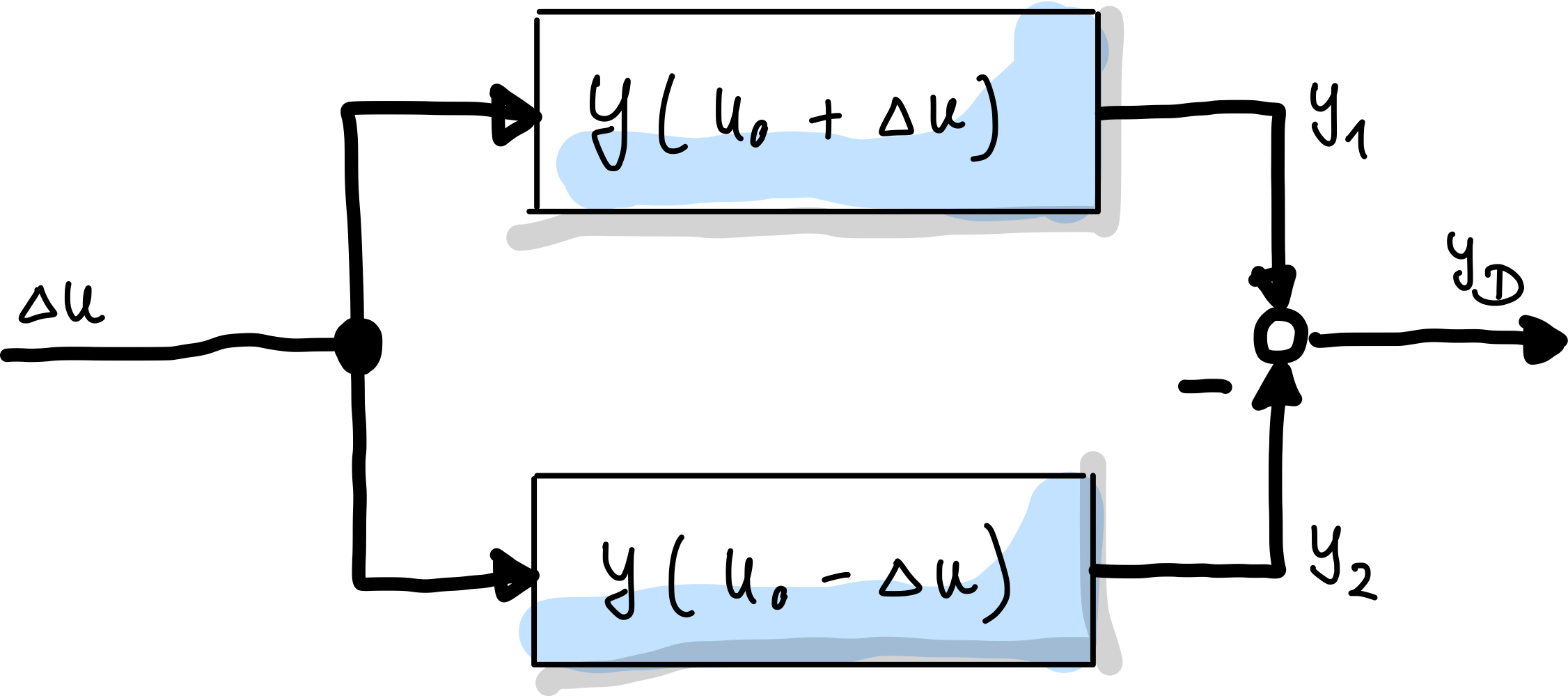
Abb. 42 Struktur eines differentiellen Systems.#
Gegenkopplung#
Um eine wirklich nahezu ideale Kennlinie zu erreichen muss das Prinzip der Gegenkopplung angewendet werden. Hierbei wird der Messkreis geschlossen, und wir haben keine einfache Messkette mehr. Die Messgröße \(u\) am Anfang der Messkette wird mit dem Ausgangssignal \(y\) verglichen, bzw. \(K(y)\), da möglicherweise eine Verstärkung vorliegt. Die Differenz \(u-K(y)\) sollte gleich Null sein, dann hat man ein System mit Kompensationsverfahren. Hierfür benötigt man jedoch ein Übertragungsglied ebenfalls im Rückkopplungspfad für \(K(y)\), da man \(y\) in das gleiche physikalische Größe wie die Messgröße umwandeln muss.
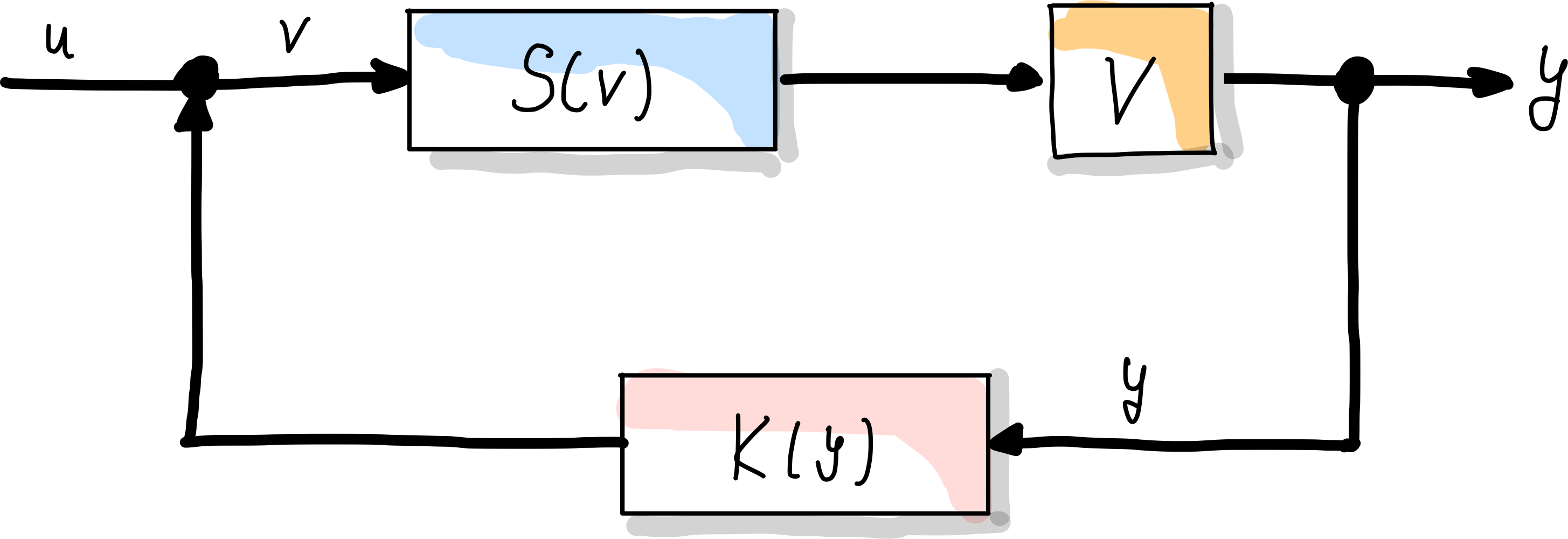
Abb. 43 Struktur eines Gegenkopplungs- und Rückkopplungssystems.#


