Piezoelektrische Sensoren

Unter Kraft- oder Druckeinwirkung wird in bestimmten Materialien, wie z.B. Quarzen, eine Ladungsumverteilung generiert, wie als Spannung gemessen werden kann. Dadurch können Kräfte und Drücke anhand einer Spannungsmessung beobachtet werden.

Abb. 114 Piezoelektrischer Kristall mit Ladungsverteilung (a). In (b) sind die positiven und negatigen Ladungsschwerpunkte eingezeichnet, die ohne externe Krafteinwirkung am gleichen Punkt vereint sind und noch kein Dipolmement und somit keine Spannung erzeugen.

Grundlagen

In pieozoelektrischen Stoffen, wie z.B. Quarzen, sind positive und negative Ladungen im Kristall zunächst ungleich verteilt, man nennt sie daher auch polarisiert. Wird der Stoff oder Quarz nun deformiert, so ändert sich das sogenannte Dipolmoment, was durch die unterschiedlichen Ladungsträger hervor gerufen wird. Dies ändert widerum die Polarisation und setzt weitere Ladungsträger an der Oberfläche des Stoffes frei. Die Menge der freien Ladungsträger, \(Q\), is propotional zur Kraft, \(F\):

\[Q = k_P \cdot F\]

wobei \(k_P\) eine materialspezifische Konstante, die unter Umständen auch von der Geometrie des Quarzes und den angebrachten Elektroden abhängt. Die so erzeugte Ladung führt an zwei Elektroden, die entsprechend am Quarz angebracht sind, zu einer elektrischen Spannung \(U\)

\[U = \frac{Q}{C} = \frac{k_P \cdot F}{C}\]

und folgt dem Gesetz eines Kondensators mit der Kapazität \(C\).

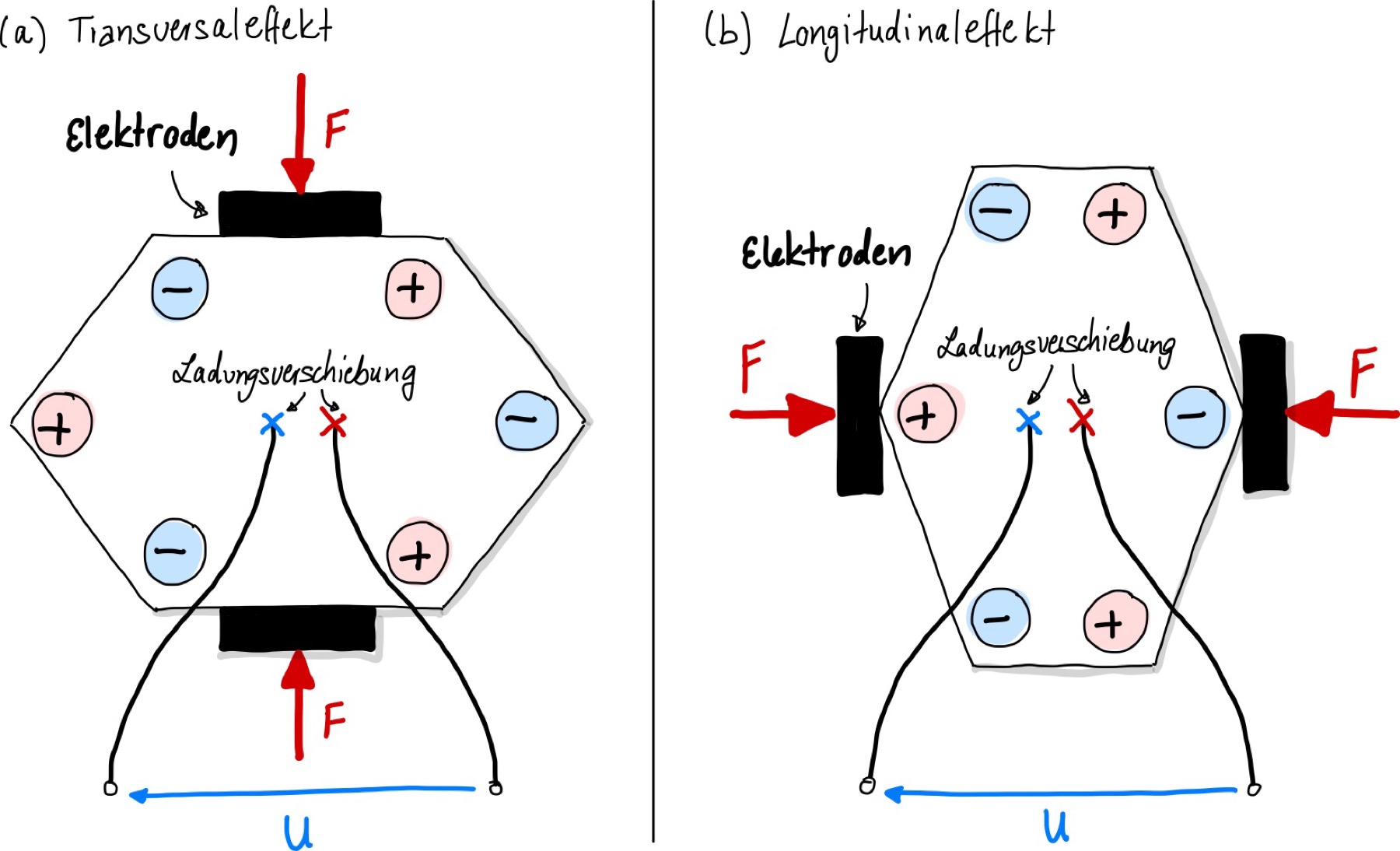
Abb. 115 Longitudinal- und Transversaleffekt in einem Piezoelektrischen Sensor.

Bei dem Anbringen der Elektroden muss auf deren Orientierung geachtet werden die davon abhängig ist, ob man den Longitudinaleffekt, Schub-/Schereffekt oder Transversaleffekt (Quereffekt) ausnutzen möchte. Auch die Richtung der Krafteinwirkung muss hierbei natürlich berücksichtigt werden. Longitudinal- und Schubeffekte sind von der Geomtrie unabghängig und \(k_P\) ist eine rein materialspezifische Konstanten. Beim Transversaleffekt kann der \(k_P\)-Wert verändert werden, indem die Fläche und Dicke des Quarzes geändert werden. Möchte man z.B. die Empfindlichkeit erhöhen, also die Verstärkung \(k_P\) vergrößern, so würde man die Fläche vergrößern und die Quarzdicker verkleinern.

Dadurch können Messbereiche von etwa 1N bis hin zu mehreren MN erreicht werden und haben im Gegensatz zu DMSs eine höhere Empfindlichkeit, sind jedoch auch teurer.

Das so generierte Messsignal \(U\) bleibt jedoch nicht dauerhaft erhalten, auch wenn weiterhin eine Kraft \(F\) einwirkt. D.h. ein piezoelektrischer Sensor erzeugt unter einer Krafteinwirkung \(F\) nur einmalig (!) eine Ladungsträgermenge \(Q\) und somit eine messbare Spannung \(U\), die danach sofort wieder abfällt. Das liegt daran, dass die Ladung über den Innenwiderstand des Quarzes über eine bestimmte Zeit \(t\) abfällt:

\[t = R_i C_i\]

wobei \(R_i\) und \(C_i\) der Innenwiderstand und -Kapazität des Quarzes sind. Typische Werte liegen hier bei \(R_i \approx 10^{12}\,\Omega\) und \(C_i \approx 10\,\mathrm{pF}\), wodurch das Messsignal um die \(t = 10\,\mathrm s\) gespeichert wird. Werte von 10 Milisekunden bis hin zu mehreren Stunden sind hierbei möglich.

Zusammengefasst bedeutet dies, dass Piezoelektrische Kraftsensoren zwar höhere Empfindlichkeiten haben, aber sich nicht für statische Kraftmessungen eignen, da sich die Kraft kontinuierlich ändern muss um ein Spannungssignale abgreifen zu können. Piezoelektrische Kraftsensoren haben im Unterschied zu einem DMS außerdem praktisch keine Längenänderung und verformen sich nur minimal, weshalb sie über große Messbereiche gut funktionieren.

Spannungsmessung

Die Spannungsmessung an einem piezoelektrischen Sensor kann mitunter sehr anspruchsvoll sein, da Quarze sehr hohe Innenwiderstände aufweisen. Spannungsmesseingänge haben mitunter kleinere Innenwiderstände was dazu führt, dass hier keine Spannung mehr abfallen würde und somit keine Spannung messbar ist.

Abb. 116 Ersatzschaltbild der Spannungsmessung an einem piezoelektrischen Sensor.

Hierbei gilt zu beachten, dass alle Kapazitäten, die im Messsystem auftregen, miteinbezogen werden, wie es im Ersatzschaltbild in Abb. 116 dargestellt ist.

• \(C_P\) ist die Kapazität des Piezosensors

• \(C_L\) ist die Kapazität der Anschlussleitung (Kabel)

• \(C_e\) ist die Eingangskapazität der Verstärker-Schaltung

Da es sich um eine Parallelschaltung von Kondensatoren handelt wird die Gesamtkapazität wiefolgt beschrieben:

\[C_\mathrm{ges} = C_P + C_L + C_e\]

und es folgt:

\[U = \frac{k_P \cdot F}{C_P + C_L + C_e}\]

Das heißt das vorliegende Messsignal (in Form der Spannung \(U\)) ist abhängig von der internen Verschaltung und der verwendeten Komponenten und muss erneut kalibriert werden, wenn Komponenten ausgetauscht werden. Außerdem besteht die Gefahr die Empfindlichkeit zu verändern, wenn externe Kapazitäten noch hinzu kommen, z.B. aufgrund weiterer unvermeidbarer Anschlussleitungen.

Für das Ersatzschaltbild können wir erneut die Zeitkonstanten \(t\) bestimmen:

\[t = R_\mathrm{ges} \cdot C_\mathrm{ges} = \frac{R_P \cdot R_e}{R_P + R_e} \cdot (C_P + C_L + C_e)\]

Um zu vermeiden, dass sich die Ladung sofort über \(R_P\) und \(R_e\) ausgleicht müssen diese beiden Widerstände sehr hoch-ohmig sein. Die Messung von dynamischen Kräften wird bevorzugt, doch auch stationäre Prozesse können gemessen werden, wenn man die Zeitkonstante \(t\) beachtet.

Elektrometer

Für die Spannungsmessung eignen sich sogenannte Elektrometer-Schaltungen, wie sie in Kapitel Operationsverstärker behandelt wurden. Diese verfügen aufgrund ihres internen Aufbaus über sehr hohe Eingangswiderstände. Neben den eben erwähnten Innenwiderständen und -kapazitäten kommen hier nun doch die Widerstände \(R_1\) und \(R_2\) für die Verstärkerschaltung hinzu, wie in Abb. 117 dargestellt.

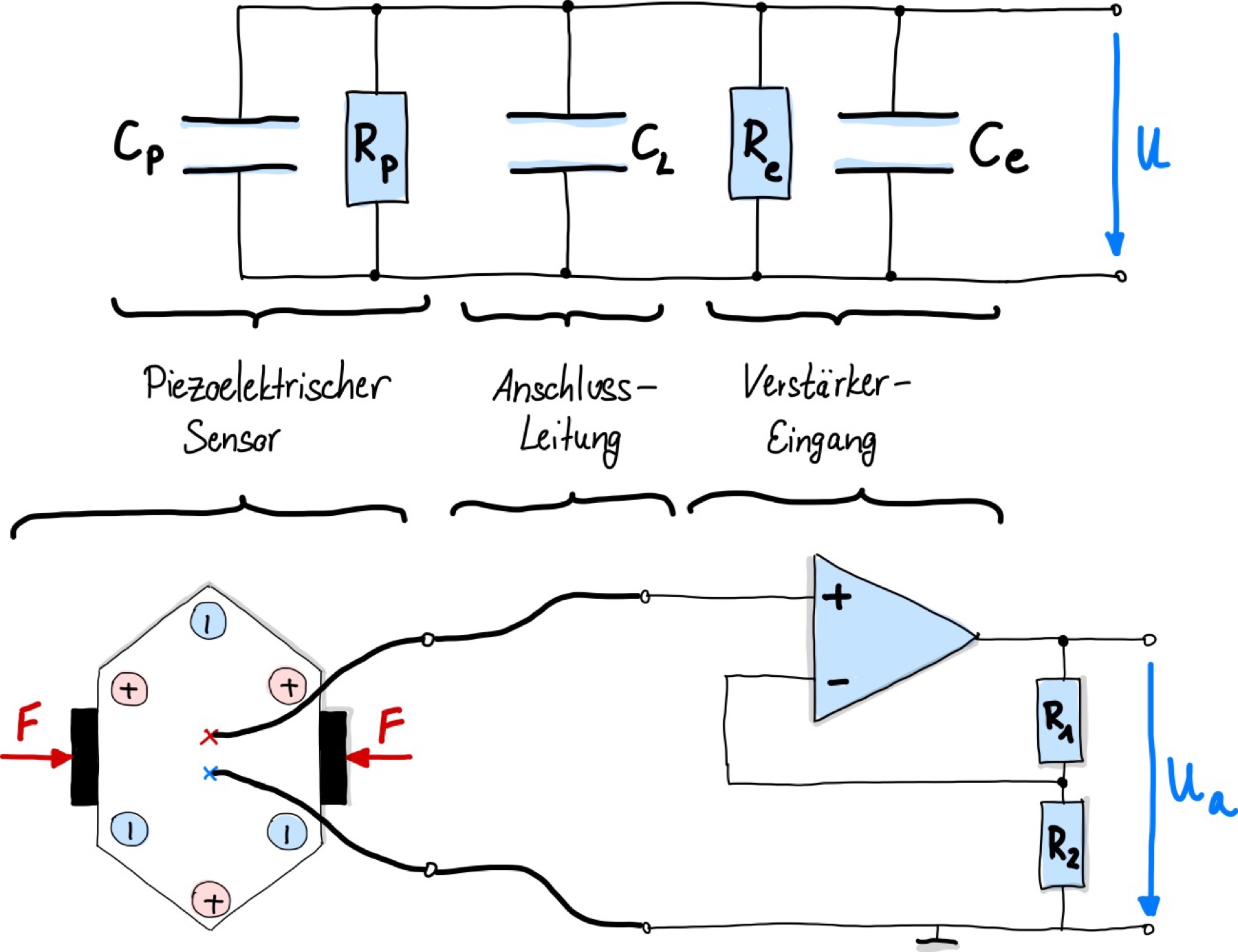
Abb. 117 Ersatzschaltbild der Elektrometer-Schaltung an einem piezoelektrischen Sensor.

Es gilt wie bisher

\[C_\mathrm{ges} = C_P + C_L + C_e\]

und

\[R_\mathrm{ges} = \frac{R_P \cdot R_e}{R_P + R_e} \rightarrow \infty\]

Dadurch folgt für die Ausgangsspannung \(U_a\) am OP-Ausgang:

\[U_a = U \cdot \left( 1 + \frac{R_2}{R_1} \right) = \frac{Q}{C_\mathrm{ges}} \cdot \left( 1 + \frac{R_2}{R_1} \right) = \frac{k_P \cdot F}{C_\mathrm{ges}} \cdot \left( 1 + \frac{R_2}{R_1} \right)\]

Ladungsverstärker

Eine weitere Möglichkeit bieten sogenannten Ladungsverstärker, die häufig mit dem Sensor direkt zusammen verkauft werden. Hierbei handelt es sich um eine Integratorschaltung, die wieder mittels einem Operationsverstärker realisiert wird. Die Idee bei dieser Methode ist, dass sie dank ihres sehr niederigen Eingangswiderstands alle freien Ladungsträger sofort aufnimmt, dem Quarz entzieht und diese auf einen internen Kondensator mit Kapazität \(C_B\) abspeichert.

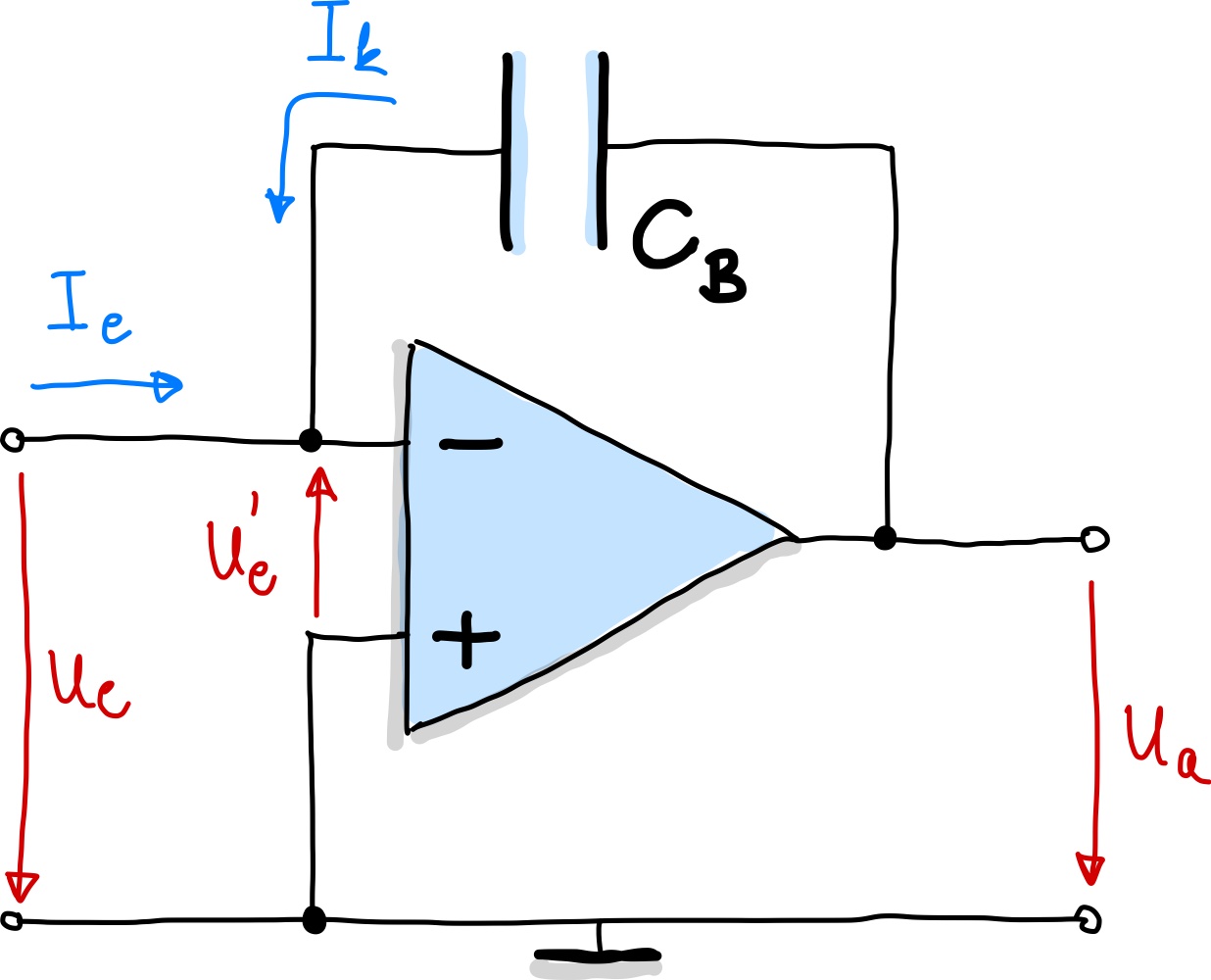
Abb. 118 Ladungsverstärker mittels Operationsverstärkerschaltung.

Der Eingangsstrom \(I_e\) wird von der zeitlich-veränderten Ladungsverschiebung im Piezoelektrischen Sensor hervorgerufen

\[I_e = \frac{dQ}{dt}.\]

Der Strom \(I_k\) wird von der Ausgangsspannung des OPs abgeleitet, welche durch den Kondensator \(C_B\) abgegriffen wird:

\[I_k = C_B \cdot \frac{dU_a}{dt}\]

Mit der Knotenregel folgt

\[I_e + I_k = 0 \Rightarrow -I_e = I_k\]

Einsetzen der obigen Formeln liefert:

\[- \frac{dQ}{dt} = C_B \cdot \frac{dU_a}{dt}\]

Integrieren beider Seiten führt zu:

\[- \int \frac{dQ}{dt} dt = C_B \cdot \int \frac{dU_a}{dt} dt\]

Integrale lösen führt zu:

\[- Q = C_B \cdot U_a\]

Damit folgt für die Ausgangsspannung:

\[U_a = \frac{-Q}{C_B} = - \frac{k_P \cdot F}{C_B}\]

D.h. dadurch wären auch quasi-statische Kraftmessungen prinzipiell möglich. Die Empfindlichkeit und Driftzeit kann über die Kapazität \(C_B\) eingestellt werden. Die Kapazitäten von Piezosensor, Leitung und Verstärkereingang sind vernachlässigbar. Nachteil dieser Schaltung ist jedoch, dass nur Wechselgrößen gemessen werden können (dynamische Kraftänderungen), da andernfalls keine Ladungsänderung über die Zeit auftritt und somit kein Messsignal abgreifbar ist.

Empfindlichkeit

• SiO2 (Quarz) ist ein Einzelquarzelement für den \(k_P = 2,3 \cdot 10^{-12}\,\mathrm{As/N}\) im Longitudinaleffekt beträgt.

• Ein weiteres sehr häufig benutztes piezoelektrisches Material ist Bariumtitant (BaTiO3) mit \(k_P = 250 \cdot 10^{-12}\,\mathrm{As/N}\).

Für beide Systeme können die Empfindlichkeiten berechnet werden, indem die obige Kennlinie abgeleitet wird:

\[E = \frac{U_a}{F} = \frac{k_P}{C}\]

Für eine Gesamtkapazität der Messschaltung von \(C=120\,\mathrm{pF}\) ergeben sich Empfindlichkeiten von

• SiO2: \(E = 19,2\,\mathrm{V/kN}\)

• BaTiO3: \(E = 2,08\,\mathrm{kV/kN}\)

Referenzen