Spannungsmesseingang

In Abb. 70 ist dargestellt, wie elektrische Spannungen gemessen werden. \(R_L\) stellt hierbei einen Lastwiderstand, z.B. den einen Motors oder eines anderen Verbrauchers, dar.

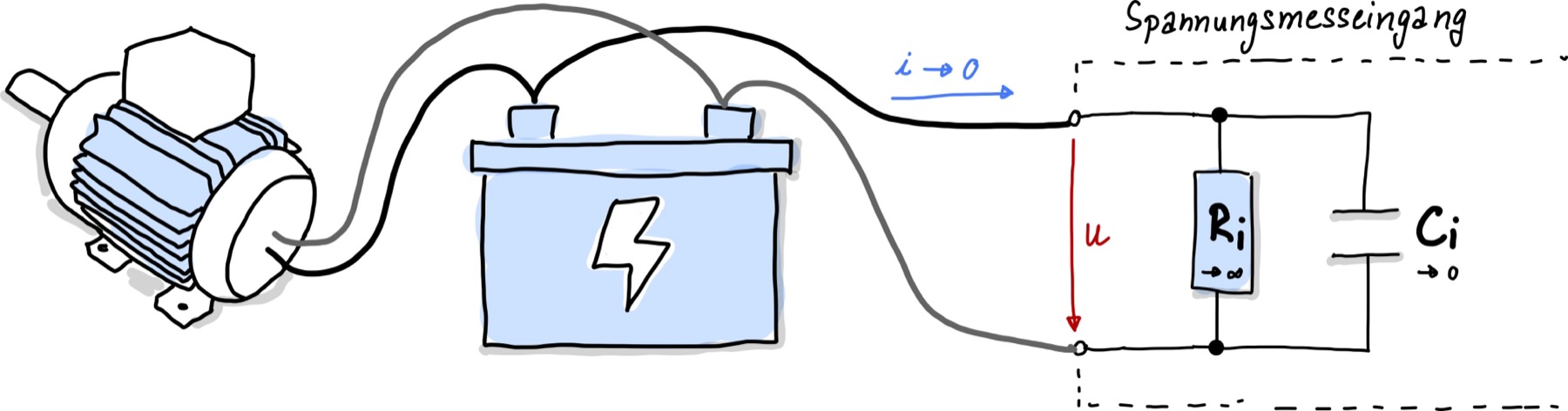
Abb. 70 Schaltung zur Messung elektrischer Spannungen.

Um den Motor zu betreiben wird eine Spannung angelegt. Parallel zu dieser angelegten Spannung wird der Spannugnsmesseingang angelegt. Dies gilt immer, egal ob es sich um eine Wechsel- oder Gleichspannung handelt.

Den Spannungsmesseingang wurde mittels eines Ersatzschaltbildes dargestellt und kann aus einer Parallelschaltung eines ohmschen Widerstands, \(R_i\) (der sogenannte Innenwiderstand), und einer Kapazität, \(C_i\), beschrieben werden. \(R_i\) und \(C_i\) sind nicht wirklich in dieser Anordnung so aufgebaut, sie resultieren vielmehr aus den elektrischen Eigenschaften der verbauten Bauelemente und werden durch den Hersteller des zugehörigen Messsystems spezifiziert.

Ziel bei der Spannungsmessung ist es zu erreichen, dass möglichst kein Strom durch den Spannungsmesseingang ließt. Das bedeutet, dass der Hersteller des Spannungsmessgeräts einen möglichst hohen Innenwiderstand \(R_i\) wählen wird. Typischerweise liegt \(R_i\) zwischen \(1-10\,\mathrm{M\Omega}\).

Gleichspannungsmessung

Bei Gleichspannungsmessungen spielt die Innenkapazität \(C_i\) keine Rolle. Die recht kleine Kapazität lädt sich sofort nach Anlegen der zu messenden Gleichspannung auf und hat ab dann keinerlei Einfluss mehr auf die Messung.

Die Bedeutung der Innenwiderstände eines Messeingangs hängt von der Schaltung ab, die vermessen werden soll. Als Beispiel soll eine einfache Spannungsteilerschaltung aus der Reihenschaltung von zwei Widerständen \(R_1\) und \(R_2\), wie in Abb. 71 dargestellt, dienen.

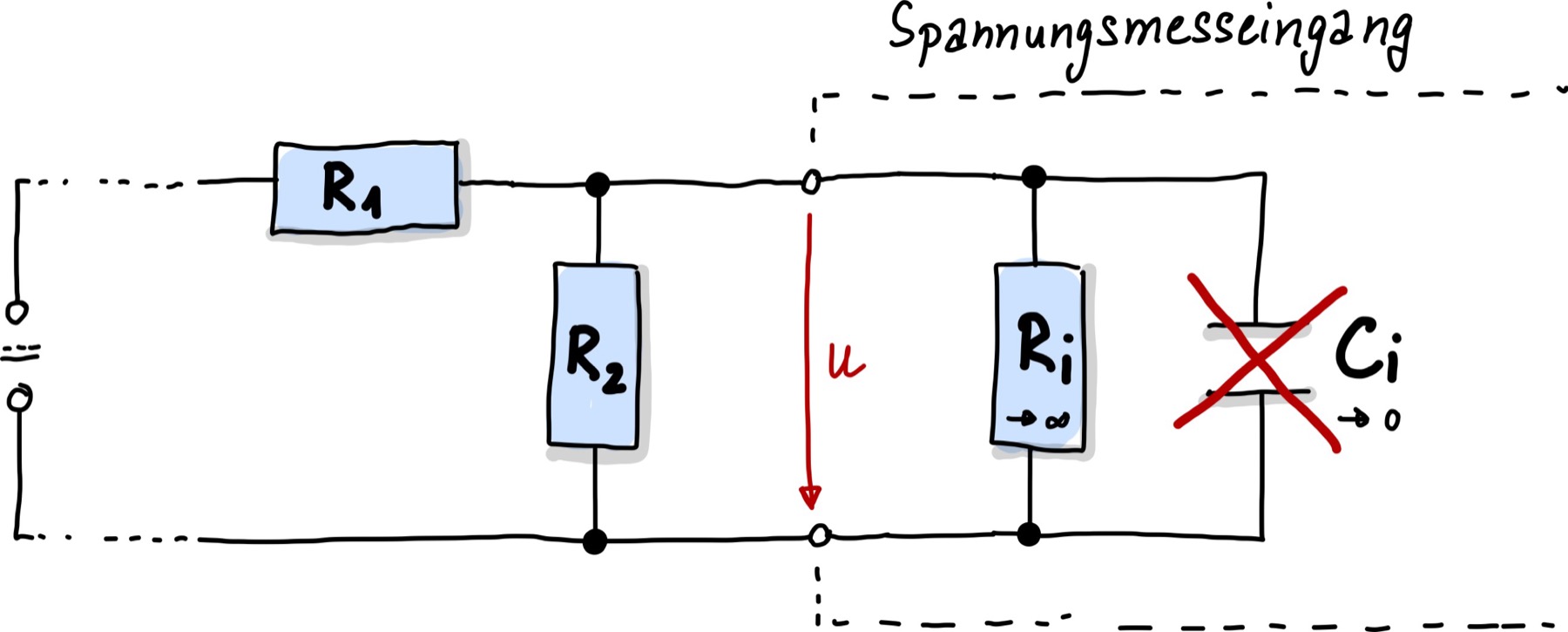
Abb. 71 Spannungsmesseingang an einer Schaltung mit Gleichspannung.

Man nehme an, beide Widerstände sind gleich, d.h. \(R_1 = R_2 = R\). Dann berechnet sich das Spannungsteilerverhältnis wiefolgt:

\[r = \frac{R_2}{R_\mathrm{ges}} = \frac{R_2}{R_1 + R_2} = \frac{R}{2R} = 0{,}5\]

Die Spannung wird genau geteilgt. Wird nun ein Spannungsmesseingang angeschlossen, so wird ein weiterer Widerstand \(R_i\) parallel zu \(R_2\) geschaltet:

\[R_\mathrm{2,ges} = \frac{R_2 \cdot R_i}{R_2 + R_i}\]

Der Gesamtwiderstandswert ist nun die Reihenschaltung aus \(R_1\) und \(R_\mathrm{2,ges}\). Daraus folgt für das Spannungsteilerverhältnis:

\[r = \frac{R_\mathrm{2,neu}}{R_\mathrm{ges,neu}} = \frac{R_i}{R + 2R_i}\]

Je kleiner \(R_i\), desto größer ist die Messabweichung, wie folgendes Beispiel zeigt. Je kleiner \(R\) (Widerstände im Schaltkreis), desto kleiner die Messabweichung.

Das Spannungsteilerverhältnis hat sich verändert, obwohl die eigentlich Schaltung, bestehend aus \(R_1\) und \(R_2\) nicht verändert wurde. Das Verhältnis zu klein gemessen. Da es sich hierbei um einen systematischen Fehler handelt, kann mittels Kenntnis des Innenwiderstandes das Spannungsteilerverhältnis korrigiert werden.

Beispiel

Bestimme die Messabweichung von \(u\), die bei der Spannungsmessung an einem Spannungsteiler mit \(R_1 = R_2 = 100\,\mathrm{k\Omega}\) auftritt. Der Innenwiderstand beträgt \(R_i = 1\,\mathrm{M\Omega}\), bzw. \(R_i = 10\,\mathrm{M\Omega}\).

Der Wert für \(R_2\), nämlich \(100\,\mathrm{k\Omega}\) ist im Vergleich zum Innenwiderstand von \(R_i = 1\,\mathrm{M\Omega}\) sehr viel kleiner. D.h. wir bestimmen zunächst den Widerstandswert der Parallelschaltung bestehend aus \(R_2\) und \(R_i\):

\[R_\mathrm{2||i} = \frac{R_2 \cdot R_i}{R_2 + R_i} \approx 90{,}9\,\mathrm{k\Omega}\]

Dies ist schon mal etwas kleiner als der eigentlich Wert von \(R_2\). Ohne Anlegen eines Messeingangs liegt das klassische Spannungsteilerverhältnis von

\[r_0 = \frac{R_2}{R_1+R_2} = 0{,}5\]

Mit Messeingang liegt es bei:

\[r_1 = \frac{R_\mathrm{2||i}}{R_1+R_\mathrm{2||i}} = 0{,}48\]

Eine zu messende Spannung von \(u=10\,\mathrm V\) würde entsprechend verringert ausfallen:

\[\frac{r_1}{r_0}\cdot u = 9{,}523\,\mathrm{V}\]

Die Messabweichung beträgt -4,76% bzw. -0,476 V.

Für \(R_i = 10\,\mathrm{M\Omega}\) gehen wir analog vor und erhalten:

\[r_1 = \frac{R_\mathrm{2||i}}{R_1+R_\mathrm{2||i}} = 0{,}497\]

Die Messabweichung beträgt -0,497% bzw. -0,0497 V.

Show code cell source Hide code cell source

R_1 = 10e3
R_2 = 10e3
R_i = 10e6
u = 10

r_0 = R_2 / (R_1 + R_2)
R_ges = (R_2 * R_i) / (R_2 + R_i)
r_1 = R_ges / (R_1 + R_ges)

print('Innenwiderstand der Parallelschaltung aus R_2 und R_i: ', R_ges/1000, 'kOhm')
print('Klassisches Spannungsteilerverhältnis ohne Messeingang: ', r_0)
print('Spannungsteilerverhältnis mit Messeingang: ', r_1)
print('Verhältnis der beiden Verhältnisse zueinander: ',  r_1/r_0)
print('Spannungsmessung bei ',u,'V eigentlicher Spannung: ', r_1/r_0*u, 'V')
print('Die Messabweichung beträgt: ', (1-r_1/r_0)*100, '% = ', r_1/r_0*u-u,'V')

Innenwiderstand der Parallelschaltung aus R_2 und R_i:  9.990009990009991 kOhm
Klassisches Spannungsteilerverhältnis ohne Messeingang:  0.5
Spannungsteilerverhältnis mit Messeingang:  0.4997501249375313
Verhältnis der beiden Verhältnisse zueinander:  0.9995002498750626
Spannungsmessung bei  10 V eigentlicher Spannung:  9.995002498750626 V
Die Messabweichung beträgt:  0.04997501249374148 % =  -0.004997501249373926 V

Wechselspannungsmessung

Erst bei der Messung von Wechselspannungen wird die Innenkapazität \(C_i\) relevant. Legt man beispielsweise eine periodische Sinusspannung an, so besitzt \(C_i\) einen Wechselstromwiderstand \(X\) (auch Blindwiderstand, Impedanz), der abhängig von der angelegten Frequenz \(f\) der Sinusspannung ist:

\[X = \frac{1}{\omega C_i} = \frac{1}{2 \pi f C_i}\]

(normalerweise steht hier noch ein Minuszeichen in der Gleichung, was wir vernachlässigen, da uns lediglich die Beträge interessieren.)

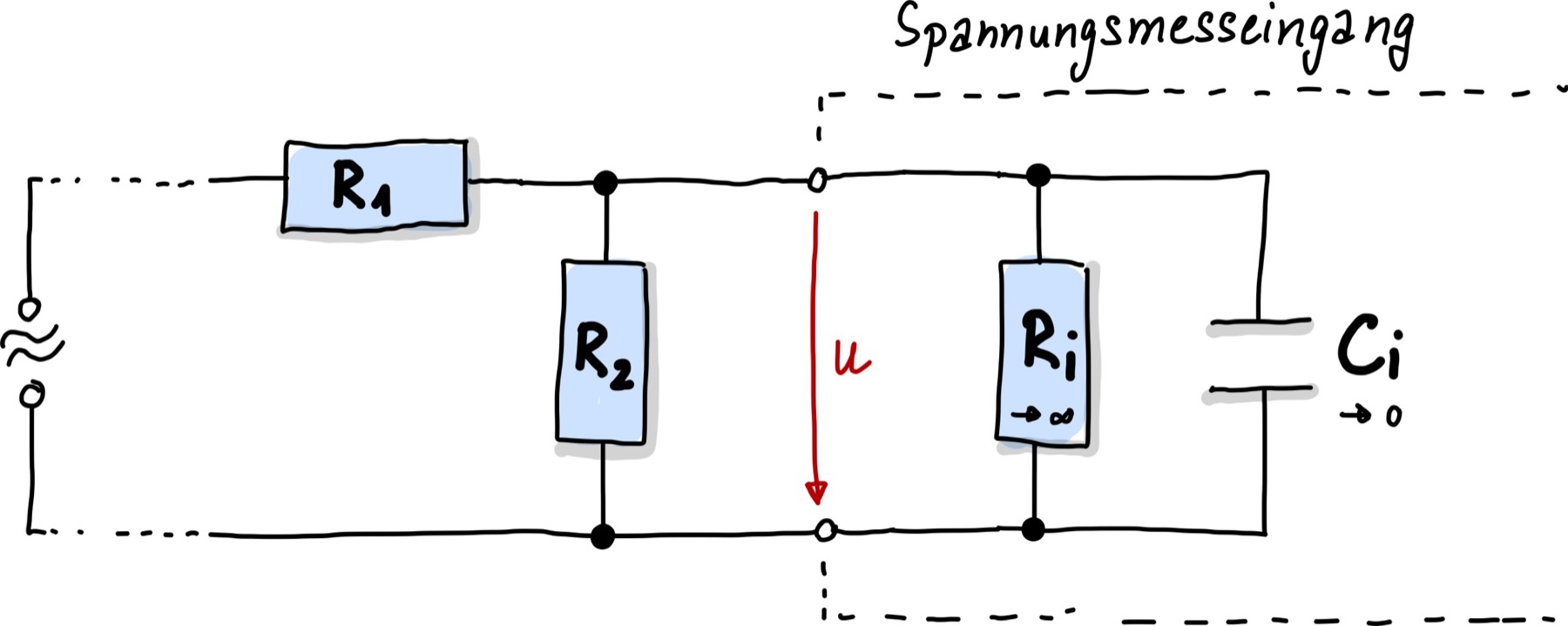
Abb. 72 Spannungsmesseingang an einer Schaltung mit Wechselspannung.

Typischerweise liegen die Werte von \(C_i\) bei etwa \(\approx 100\,\mathrm{pF}\), wenn es sich um höherwertige Messgeräte handelt.

Aufgabe

Wie hoch ist der Wechselstromwiderstand \(X\) bei einer Frequenz von \(1\,\mathrm{kHz}\)?

Nach dem Lösen der letzten Aufgabe werdet ihr feststellen, dass der Wechselstromwiderstand bei \(f=1\,\mathrm{kHz}\) etwa in der Größenordnung von \(R_i\) liegt und somit keine nennentwerte Messabweichung verursachen wird. Ein anderes Ergebnis erhalten wir, wenn wir die Frequenz auf \(f=100\,\mathrm{kHz}\) erhöhen.

Aufgabe

Wie hoch ist der Wechselstromwiderstand \(X\) bei einer Frequenz von \(100\,\mathrm{kHz}\)?

Bei Wechselspannungen sollte man zunächst immer sicherstellen, dass die Frequenz noch vom Messeingang laut Hersteller noch unterstützt wird. Da hierbei der Wechselstromwiderstand im \(\mathrm{k\Omega}\)-Bereich liegt, wird ein deutlicher Strom durch den Messeingang fließen und der Widerstand muss ebenfalls berücksichtig werden.

Aufgabe

Bestimme die Messabweichung von \(u\), die bei der Spannungsmessung an einem Spannungsteiler mit \(R_1 = R_2 = 100\,\mathrm{k\Omega}\) bei einer Wechselspannung mit einer Frequenz von \(f = 50\,\mathrm{kHz}\) und einer Amplitude von \(10\,\mathrm V\) auftritt. Der Innenwiderstand beträgt \(R_i = 1\,\mathrm{M\Omega}\) und die Innenkapazität \(C_i = 100\,\mathrm{pF}\). Im folgende Code-Block findest du wieder Hinweise auf das Vorgehen, wobei hier mit komplexen Zahlen berechnet wurde um auch die Phasenverschiebung darzustellen.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal 

# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
plt.figure(figsize=(7,3)) # Plot-Größe
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße

R_1 = 100e3
R_2 = 100e3
R_i = 1e6
u = 10
C_i = 100e-12
f = 100e3

SAMPLE_RATE = 10e6  # Hertz
DURATION = 1e-4  # mSeconds
t = np.linspace(0, DURATION, int(SAMPLE_RATE * DURATION), endpoint=False)
y = u * np.sin(2 * np.pi * f * t)

# Widerstände berechnen:
X = 1/(1j*2*np.pi*f*C_i)
r_0 = R_2 / (R_1 + R_2)
R_ges_1 = (R_2 * R_i) / (R_2 + R_i)
R_ges = (R_ges_1 * X) / (R_ges_1 + X)
r_1 = R_ges / (R_1 + R_ges)

# Frequenzgang berechnen für f
r_ampl = np.abs(r_1)
r_phase = np.arctan(r_1.imag/r_1.real)

# Sinuswelle am Ausgang:
y_out = r_ampl/r_0 * u * np.sin(2 * np.pi * f * t + r_phase)

plt.subplot(1,2,1)
plt.plot(t*1000,y, 'tab:blue',label = 'ohne Messeingang')
#plt.xlim([0,0.1])
plt.xlabel('Zeit (ms)')
plt.ylabel('Spannung (V)')
plt.legend(loc='upper right')

plt.subplot(1,2,2)
plt.plot(t*1000,y, 'tab:blue', alpha = 0.5, ls=':', label = 'ohne Messeingang')
plt.plot(t*1000,y_out, 'tab:red', lw=2, label = 'mit Messeingang')
#plt.xlim([0,0.1])
plt.xlabel('Zeit (ms)')
plt.ylabel('Spannung (V)')
plt.legend(loc='upper right')
plt.tight_layout()

print('Innenwiderstand der Parallelschaltung aus R_2, R_i und C_i: ', np.abs(R_ges)/1000, 'kOhm')
print('Klassisches Spannungsteilerverhältnis ohne Messeingang: ', r_0)
print('Spannungsteilerverhältnis mit Messeingang: ', r_ampl)
print('Verhältnis der beiden Verhältnisse zueinander: ',  r_ampl/r_0)
print('Spannungsmessung bei ',u,'V eigentlicher Spannung: ', r_ampl/r_0*u, 'V')
print('Die Messabweichung beträgt: ', (1-r_ampl/r_0)*100, '% = ', r_ampl/r_0*u-u,'V')

Innenwiderstand der Parallelschaltung aus R_2, R_i und C_i:  15.677059256043355 kOhm
Klassisches Spannungsteilerverhältnis ohne Messeingang:  0.5
Spannungsteilerverhältnis mit Messeingang:  0.1509471920753415
Verhältnis der beiden Verhältnisse zueinander:  0.301894384150683
Spannungsmessung bei  10 V eigentlicher Spannung:  3.0189438415068297 V
Die Messabweichung beträgt:  69.8105615849317 % =  -6.98105615849317 V

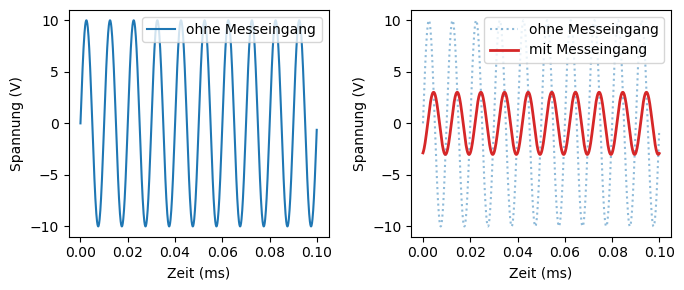
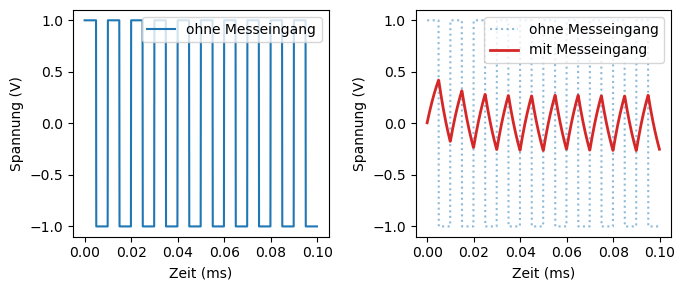
Die beiden obigen Plots zeigen, dass sich zwar wieder ein stationäres Sinussignal ergibt, die Amplitude jedoch deutlich kleiner als das ursprüngliche Signal ist. In einem realen Messsystem würde man außerdem einen Einschwingvorgang beobachten, der etwa eine Periode dauern kann. Das heißt man würde beobachten, wie die Amplitude zu Beginn noch etwas höher ist, bis sie sich auf einen konstanten Wert einpendelt. In diesem konkreten Fall erhalten eine Relativabweichung in der Spannungsmessung von 70% (!), bezogen auf den Messwert. Zusätzlich erhalten wir eine Phasenverschiebung. Dies wird aber erst wichtig, wenn Momentanmesswerte aufgenommen werden. Für die Messung eines Gleichrichtwerts oder Effektivwerts, wo ja über eine Periode gemittelt wird, ist eine Phasenverschiebung egal.

Würde man anstelle einer Sinusspannung ein Rechtecksignal anlegen, so ändert sich auch Signalform signifikant, wie es in den folgenden Diagrammen dargestellt ist. Das Rechtecksignal ähnelt nun eher einem Dreiecksignal, die Amplitude ist etwas eingebrochen, allerdings ist kaum eine Phasenverschiebung ersichtlich.

Show code cell source Hide code cell source

from scipy.signal import butter, lfilter, freqz
from scipy import signal 
plt.style.use('default') # Matplotlib Style wählen
plt.figure(figsize=(7,3)) # Plot-Größe
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße

f = 100e3
SAMPLE_RATE = 10e6  # Hertz
DURATION = 1e-4  # mSeconds
t = np.linspace(0, DURATION, int(SAMPLE_RATE * DURATION), endpoint=False)

y = signal.square(2 * np.pi * f * t)

def butter_lowpass(cutoff, FS, order=5):
    nyq = 0.5* FS
    normal_cutoff= cutoff/nyq
    b,a = butter(order, normal_cutoff, btype = 'low', analog = False)
    return b,a

def butter_lowpass_filter(data, cutoff, FS, order=5):
    b,a = butter_lowpass(cutoff, FS, order=order)
    y = lfilter(b,a,data)
    return y

order = 1
cutoff = 1/(2*np.pi*R_ges_1*C_i)
y_filt = butter_lowpass_filter(y,cutoff, SAMPLE_RATE, order)

plt.subplot(1,2,1)
plt.plot(t*1000,y, 'tab:blue',label = 'ohne Messeingang')
#plt.xlim([0,0.1])
plt.xlabel('Zeit (ms)')
plt.ylabel('Spannung (V)')
plt.legend(loc='upper right')

plt.subplot(1,2,2)
plt.plot(t*1000,y, 'tab:blue', alpha = 0.5, ls=':', label = 'ohne Messeingang')
plt.plot(t*1000,y_filt, 'tab:red', lw=2, label = 'mit Messeingang')
#plt.xlim([0,0.1])
plt.xlabel('Zeit (ms)')
plt.ylabel('Spannung (V)')
plt.legend(loc='upper right')
plt.tight_layout()

Innerer Aufbau und zu berücksichtigende Messabweichungen

Die oben genannten Messabweichungen resultieren lediglich daraus, dass ein Spannungsmesseingang an eine Schaltung angeschlossen wurde, um eben eine Spannung zu messen. Hinzu kommen aber noch weitere Messabweichungen, die wie schon in den vorangegangenen Kapiteln beschrieben, berücksichtig werden müssen. Viele Spannungsmesseingänge beinhalten weitere Komponenten, wie in Abb. 73 dargestellt.

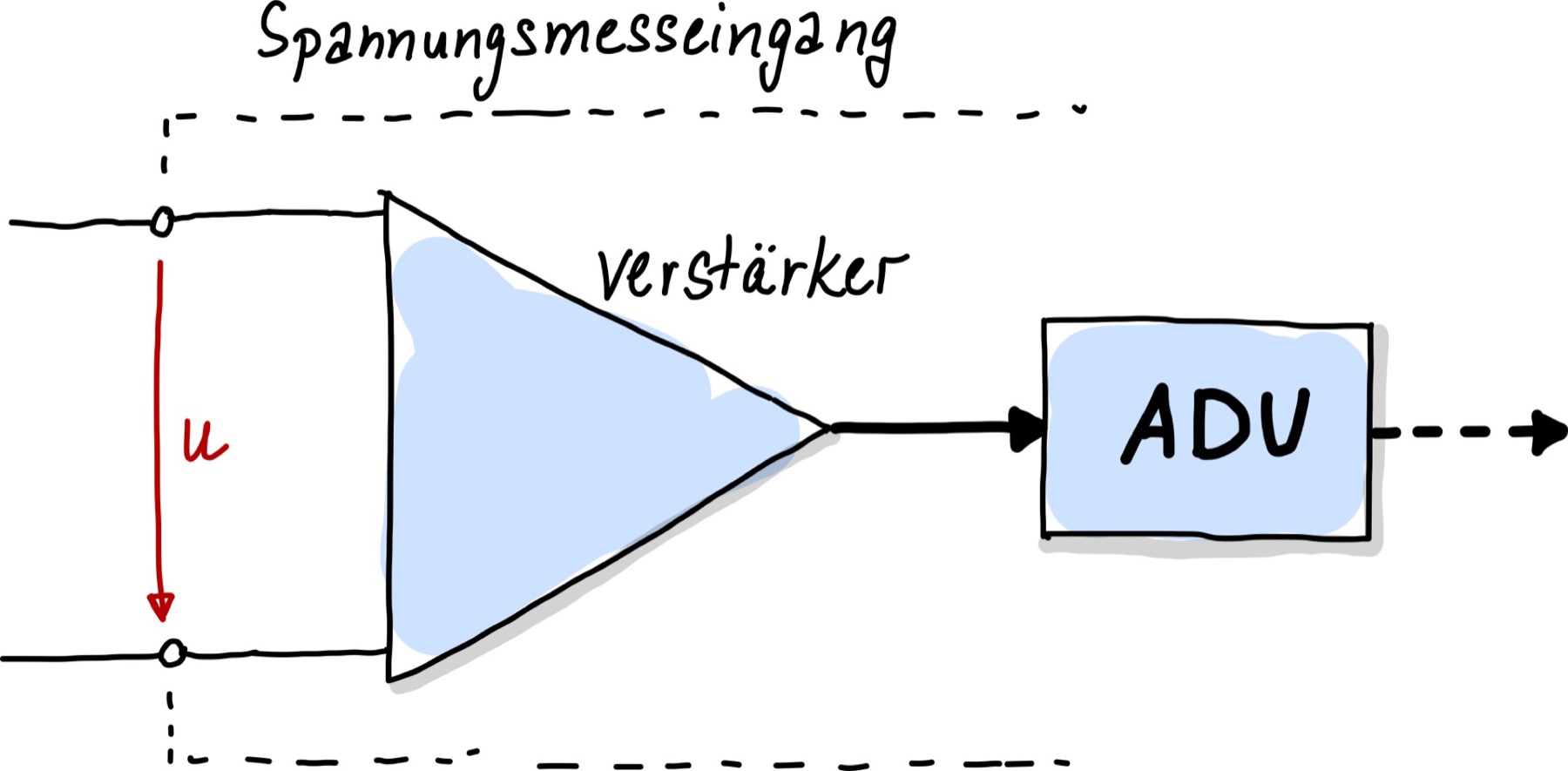
Abb. 73 Grober interner Aufbau eines Spannungsmesseingangs.

• Eine Verstärkung wird insbesondere bei kleinen Spannungssignalen (\(<1\,\mathrm V\)) benötigt. Verstärker besitzen häufig einen konkreten Frequenzgang, sodass insbesondere bei Wechselspannungen wieder besonders aufgepasst werden muss. Typischerweise nimmt der Verstärkungsfaktor mit zunehmender Frequenz ab. Auf vielen Messgeräten wird eine Maximalfrequenz spezifiziert, die unter anderem aufgrund der Verstärker-Komponente existiert.

• Die Angabe einer Grenzfrequenz oder Bandbreite eines Messsystems beinhaltet meistens nicht die Verstärkerstufe und Frequenzgänge müssen extra gemessen und abgeschätzt werden.

• Eine Dämpfung wird bei der Messung von hohen Spannungssignalen eingebaut. Im einfachsten Fall wird ein Spannungeteiler, bestehend aus 2 ohmschen Widerständen, eingebaut. Auch hier treten wieder frequenzabhängige Verhaltensweisen auf.

• Bei Messgeräten für Wechselspannungen werden u.a. auch Gleichrichter und Glättungen eingebaut, wie in Abb. 74 dargestellt.

• Ein Analog-Digital-Umsetzer (ADU) wandelt das analog variierende Eingangssignal in ein Digitalwort um. Hier treten Messabweichungen infolge die Digitalisierung auf. Einmal wird der Wertebereich diskret und es können nicht mehr beliebig kleine Messwertsprünge gemessen werden. Zudem können Aliasing-Effekte auftreten, wenn die Abtastrate unterhalb der zweifachen Nyquist-Shannon-Frequenz fällt.

• Die Abweichungen, die wir in den vorangegegangenen Abschnitten berechnet werden, können vom Gerätehersteller gar nicht angegeben werden, da hierfür immer genaue Kenntnis der Schaltung benötigt wird, an der die Spannung gemessen werden soll. Lediglich die Innenwiderstände werden spezifiziert, mittels welcher dann die Messabweichung berechnet werden muss.

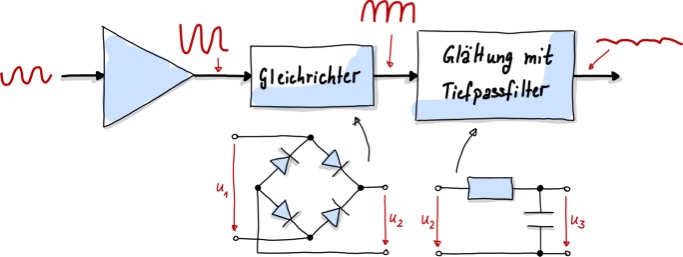
Abb. 74 Grober interner Aufbau eines Verstärkermoduls in einem Spannungsmesseingangs.

Messung des Gleichrichtswerts

Zur Messung des Gleichrichtwerts einer Wechselspannung kann eine Diodenschaltung wie in Abb. 74 benutzt werden.

Funktionsweise einer Diode

Die Diode ist ein Halbleiterbauelement, welches aus p- und n-dotierten Schichten besteht. Im Schaltbild sieht das Symbol aus wie ein Pfeil. Sie hat eine Durchlass- (in Pfeilrichtung) und eine Sperrichtung (gegen Pfeil). So ist eine Diode beispielsweise erst für 0,7V leitend, unterhalb die Schwellspannung ist sie gesperrt und leitet keinen Strom. Dies liegt an den n- und p-dotierten Schichten. Um eine Silizum-Diode herzustellen, wird Silizium zum Halbleiter verarbeitet:

• Die Anode wird mit Bor verunreinigt, wodurch dem Bor Elektronen fehlen und somit eine p-dotierte Schicht mit Elektronenmangel entsteht.

• Die Kathode wird mit Phosphor verunreinigt, welches ein Elektron mehr in der Hülle besitzt, wodurch eine n-dotierte Schicht mit **Elektronüberschuss **entsteht.

Freie Elektronen können jetzt in Richtung der Löcher diffundieren, und die Löcher diffundieren in Richtung des Elektronenüberschuss. Elektronen und Löcher treffen sich also in der Mitte und rekombinieren, wodurch dieser Bereich neutral ist. Die Ränder werden jedoch positiv bzw. negativ geladen. Durch diese Ladung am Rand werden wiederum Elektronen bzw. Löcher angezogen. Außerdem entsteht in der zentralen Zone ein elektrisches Feld, wie zwischen zwei geladenen Kondensatorplatten. Die Größe der elektrischen Feldes hängt davon ab, wie viele Elektronen und Löcher rekombiniert sind. Außerdem verstärkt das äußere elektrische Feld das elektrische Feld. Ab 0,7V wird das elektrische Feld gebrochen und aufgehoben.

Die Schwellspannung (Diffusionsspannung, Durchbruchspannung) ist die wichtigste Kenngröße einer Diode. Sie gibt an, ab welcher Spannung eine Halbleiterdiode in Durchlassrichtung leitend wird. Das bedeutet auch, dass eine Diode in Durchlassrichtung nicht immer leitend ist, sondern erst ab einer bestimmten Schwellspannung. Es spielt dabei keine Rolle, in welchem Spannungsbereich sich eine Diode befindet: Die Anode der Diode muss in Durchlassrichtung nur um die Schwellspannung positiver sein als die Kathode. Die Schwellspannung ist also als Potential zu sehen. Die Schwellspannung ist abhängig vom Halbleitermaterial und entspricht nur einem ungefähren Wert. Ein paar Beispiele häufiger Halbleitermaterialien sind:

• Germanium ~ 0,3V

• Silizium ~ 0,7V

• Selen ~ 0,6V

• Kupferoxydul ~ 0,2V In Abb. 75 sind zwei Beispiele für Dioden-Kennlinien grafisch dargestellt.

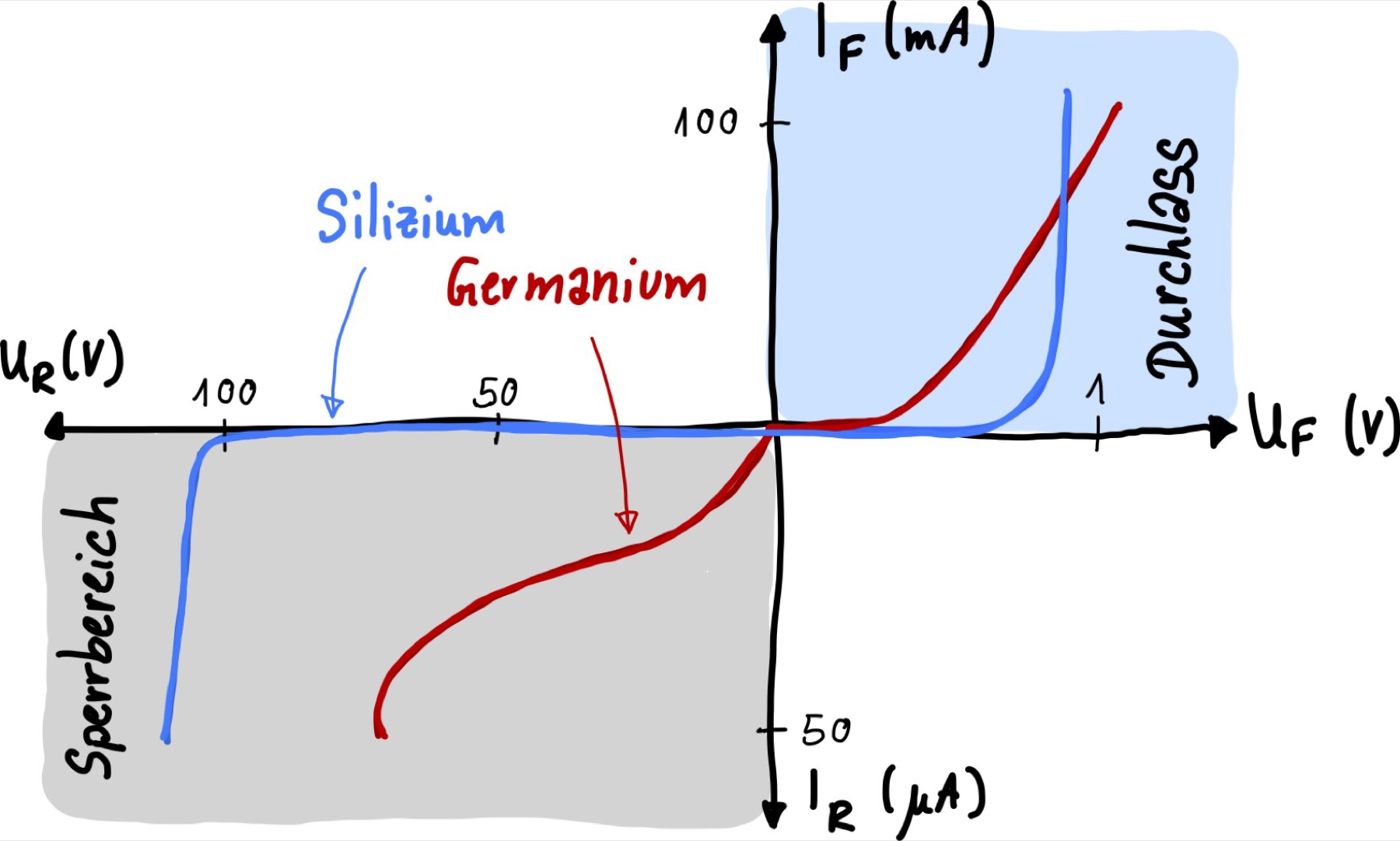
Abb. 75 Kennlinie einer Silizium und Germanium-Diode.

Hinweis: Schwellspannungen gelten nicht nur für Halbleiterdioden, sondern zum Beispiel auch für Transistoren. Hier gibt es auch einen pn-Übergang.

Bei der Silizium-Diode haben wir einen sehr kleinen Sperrstrom \(i_R\). Ab einer bestimmten Sperrspannung \(u_R\) werden die Elektronen aus ihren Kristallbindungen gelöst. Dann kommt es zum so genannten Zenerdurchbruch (Durchbruchspannung). Dabei steigt der Strom schlagartig an. Wird dieser Strom nicht begrenzt, dann zerstört sich die Diode. Bei Germanium-Dioden kommt der Zenerdurchbruch nicht zum Tragen. Dafür steigt der Sperrstrom \(i_R\) bei steigender Spannung langsam an. Ab einer bestimmten Spannung erhitzen sich die Halbleiterkristalle so stark, dass es zum Wärme-Durchbruch und zur Zerstörung kommt. Die Zerstörung der Halbleiterkristalle ist auch im Durchlassbereich möglich, wenn der maximale Strom überschritten wird.

Hierbei handelt es sich um eine Dioden-Brückenschaltung, welche in Abb. 76 skizziert ist, inklusive Spannungsverlauf.

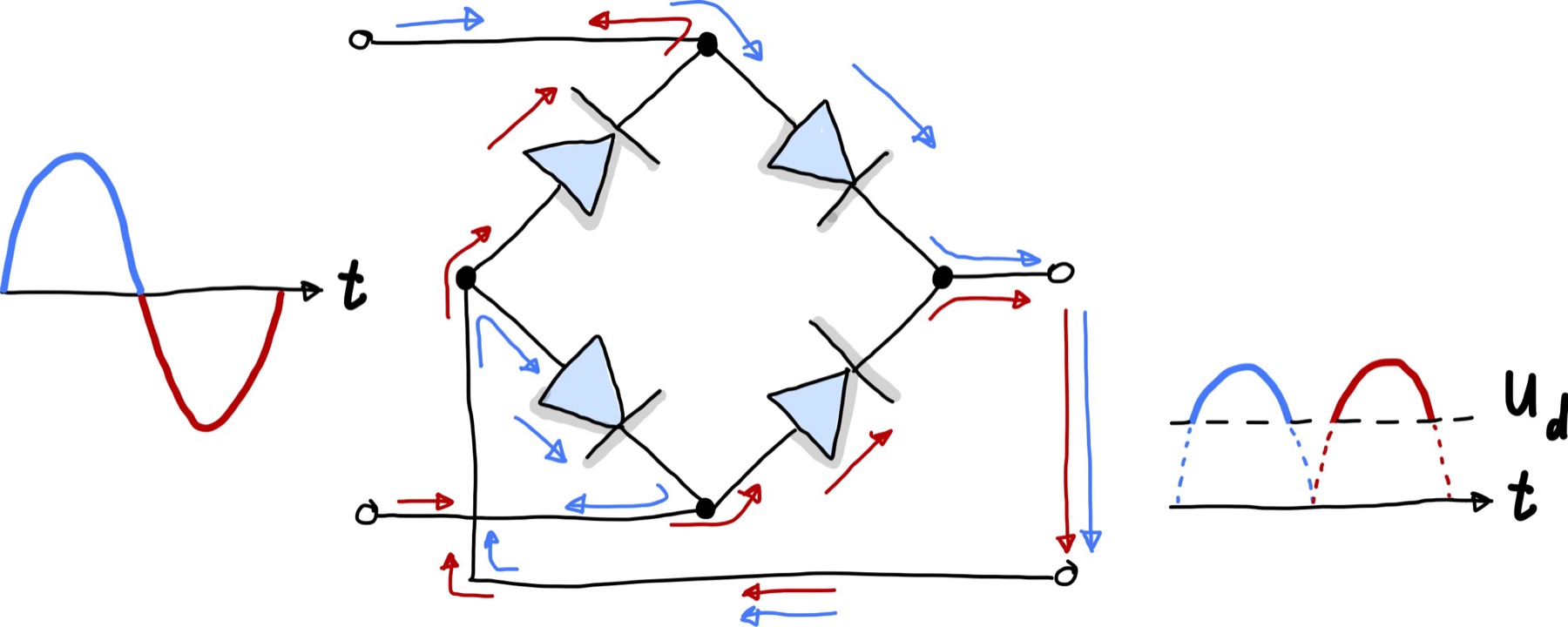
Abb. 76 Dioden-Brückenschaltung zur Messung des Gleichrichtswerts

Eine positive Eingangsspannung führt zu einem Durchfluss durch die rechte obere Diode, geht durch den Ausgang von oben nach unten und abschließend über die Diode unten links zurück. Eine negative Eingangsspannung durchfließt die anderen beiden Dioden, wobei sie den Ausgang jedoch in der gleichen Richtung verlässt, wie bei einer positiven Eingangsspannung. Der Ausgang gibt also nur positive Spannungen aus. Aufgrund der Durchbruchspannung werden außerdem kleine Spannung abgeschnitten, wodruch bei einer eingehenden Wechselspannung nur noch die Spitze der Berge, bzw. umgekehrten Täler, ausgegeben werden.

Für einen Präzisions-Gleichrichter würde man diese Grundschaltung optimieren und Operationsverstärker verwenden.

Glättung

Um den Gleichrichtwert zu erhalten, muss das Signal zusätzlich zu einer Brückenschaltung geglättet werden. Die einfachste Möglichkeit um hohe Frequenzen, also schnelle Schwingungen, abzuschwächen oder komplett loszuwerden, ist die Benutzung eines Tiefpassfilters, wie in dargestellt. Dieser besteht aus einem Widerstand \(R\) und einem Kondensator mit der Kapazität \(C\).

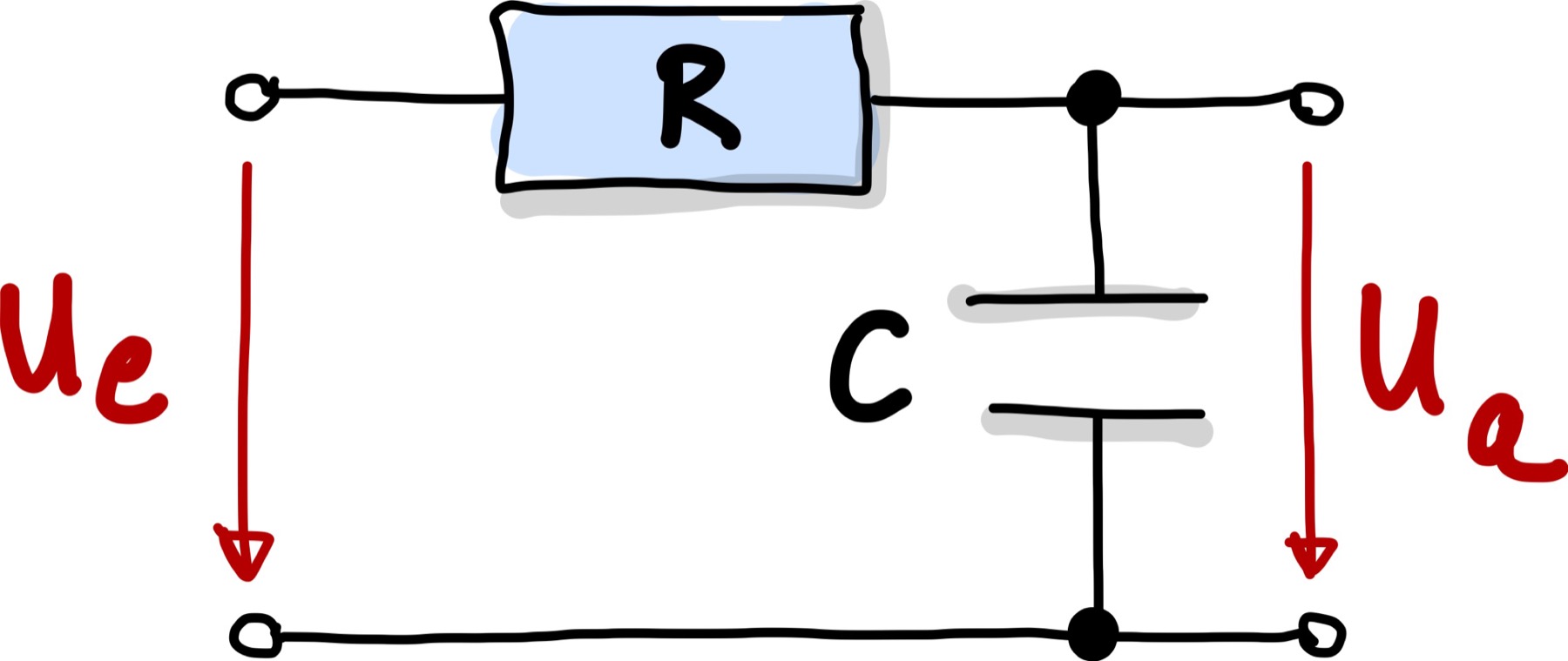
Abb. 77 Tiefpass aus R und C zur Unterdrückung hoher Frequenzen.

Diese Schaltung verzögert den Eingangsspannungsverlauf \(u_e\). Die Kondensatorspannung \(u_a\) passt sich mit einer Verzögerung aufgrund von Lade- und Entladeströme dem Eingangssignal \(u_e\) an. Die Verzögerung ist eine Art Mittelung der Eingangsspannung. Die Lade- und Entlade-Prozesse der Kondensators sind nicht beliebig schnell und können schnellen Änderungen in der Eingangsspannung nur bedingt folgen. Je schneller die Änderungen der Eingangsspannung sind, desto weniger können diese hoch-frequenten Anteile von dem System weitergegeben werden. Nur langsame Änderungen, tief-frequente Anteile, bleiben erhalten (Tiefpass).

Mit komplexere Schaltungen, bestehend aus mehreren passiven Tiefpässen (Tiefpass höherer Ordnung) oder aus aktiven Tiefpässen mit Operationsverstärken, kann der Mittelungseffekt optimiert werden.