Dehnungsmessstreifen (DMS)#

Grundlagen#

Ein Dehnungsmessstreifen (DMS) ist lediglich eine elektrische Leiterbahn, die auf einer kleinen Trägerfolie z.B. mäanderförmig aufgebracht ist, wie in Abb. 110 dargestellt. Meistens besteht diese Folie aus einem chemisch sehr robusten Material, wie z.B. Kapton (Polyimid), welches auch bei hohen Temperaturen verwendet werden kann. Hierauf wird die Leiterbahn mit einem speziellen Kleber aufgebracht, sodass diese den Oberflächendehnungen eines Körpers folgen kann. Dadurch können Dehnungen, Stauchungen, Kräfte oder Drücke auf der Oberfläche gemessen werden. Die Dehnung wird dann in Richtung des Leiterbahnabschnittes gemessen, dessen ohm’scher Widerstand sich ändert:

\[R = \frac{\rho \cdot l}{r^2 \pi}\]

\(\rho\) ist der spezifische Widerstand, der vom Material der Leiterbahn abhängt und \(l\) und \(r\) sind Länge und Radius der Leiterbahn. In der Formel wird durch die Querschnittsfläche geteilt, die näherungsweise dem kreisförmigen Querschnitt \(A = \pi r^2\) entspricht.

dms

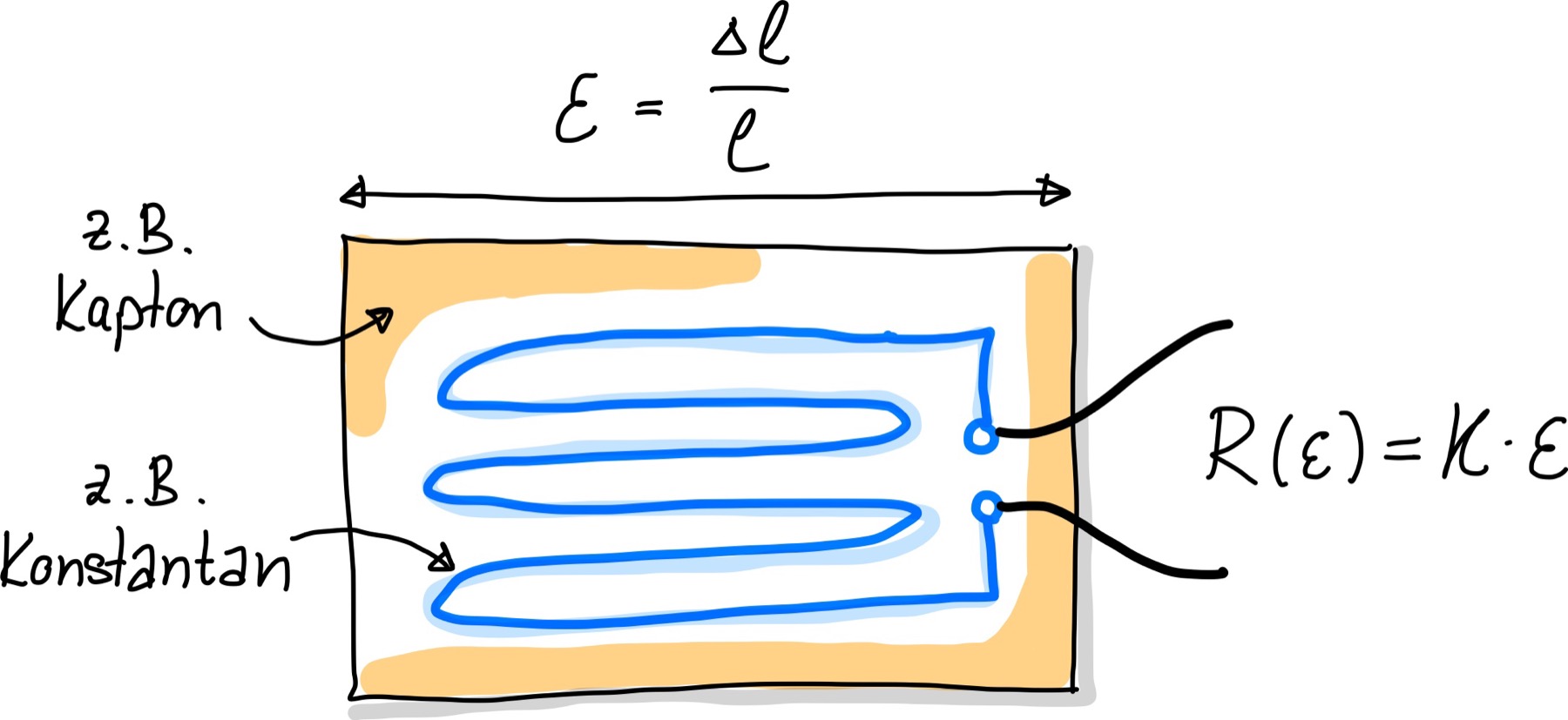
Abb. 110 Dehnungsmessstreifen (DMS).#

Für

  • Leiter ist \(\rho < 100\,\mathrm{\frac{\Omega mm^2}{m}}\),

  • Halbleiter liegt \(\rho\) zwischen \(100\,\mathrm{\frac{\Omega mm^2}{m}}\) bis \(10^{12}\,\mathrm{\frac{\Omega mm^2}{m}}\),

  • Isolatoren oder Nichtleiter ist \(\rho > 10^{^12}\,\mathrm{\frac{\Omega mm^2}{m}}\)

Als Material für die Leiterbahn wird beispielsweise Konstanten, eine Legierung aus 55% Cu, 44% Ni, 1 % Mn, verwendet, deren spezifischer Widerstand kaum von der Temperatur abhängt und \(\rho = 0,5\,\mathrm{\frac{\Omega mm^2}{m}}\) beträgt.

Nehmen wir nun, dass es sich um sehr kleine Änderungen handelt, können wir die obige Gleichungs wieder mittels Taylor-Entwicklung abschätzen, wie wir es auch bei der Fehlerfortpflanzung gemacht haben:

\[\frac{\Delta R}{R} \approx \frac{\Delta \rho}{\rho} + \frac{\Delta L}{L} - 2\cdot \frac{\Delta r}{r} = \left( \eta + 1 + 2\cdot \mu\right) \cdot \epsilon = k\cdot \epsilon\]

wobei

\[\epsilon = \frac{\Delta l}{l}\]

die Dehnung \(\epsilon\) des zu untersuchenden Stücks ist,

\[\mu = - \frac{\frac{\Delta r}{r}}{\frac{\Delta l}{l}} = - \frac{\frac{\Delta r}{r}}{\epsilon}\]

die Poisson-Zahl \(\mu\) und:

\[\eta = \frac{\frac{\Delta \rho}{\rho}}{\frac{\Delta l}{l}} = \frac{\frac{\Delta \rho}{\rho}}{\epsilon}\]

die Änderung des spezifischen Widerstands.

\(k\) ist der K-Faktor und ist für Konstantan 2,05:

\[k = 1 + 2\mu + \eta\]

Die Änderung des spezifischen Widerstands, \(\eta\), ist für die Bestimmung der \(k\)-Faktors meist vernachlässigbar:

Schon bei kleinen Dehnungen, minimalen Kräften oder anderen kleinen Belastungen ändert sich der Widerstandswert, wenn auch nur wenig, und wird mit dem \(k\)-Faktor skaliert. Typische Widerstandswerte im Grundzustand sind \(100-1000\,\Omega\), welcher sich je nach \(k\)-Faktor für Dehnungsänderungen im Promille-Bereich ebenfalls um nur diesen kleinen Betrag ändert. Aus diesem Grund werden DMSs häufig Widerstands-Messbrücken verwendet. Mittels verschiedenen Anordnungen können damit auch Querkräfte, Scherkräfte und andere Belastungen gemessen werden und Kompensation in Bezug auf Temperaturempfindlichkeiten können dadurch eliminiert werden [Par].

Anwendungen und Beispiel#

  • Kraft (und somit auch Beschleunigung)

  • Waagen (Haushaltswaagen bis hin zu Kranwaagen)

  • Druck

  • Drehmoment

  • Verformungsmessungen (experimentelle Beanspruchungsanalyse, Spannungsanalyse) auf vielen Werkstoffen

    • Biegung

    • Druck und Zug

    • Scherkräfte

Beispiel

Ein unbekannter Metalldraht hat die Länge \(l = 2\,\mathrm m\) und einen Querschnitt von \(A = 0,01\,\mathrm{mm^2}\). Die Testspannung beträgt \(U=2\,\mathrm V\) und wir messen einen Strom von \(I = 0,75\,\mathrm A\). Wie hoch ist der spezifische Widerstand des Metalldrahtes?

Lösung

\[\rho = \frac{R\cdot A}{l} = \frac{U \cdot A}{I \cdot l} = \frac{3,5\,\Omega \cdot 0,01\,\mathrm{mm^2}}{2\,\mathrm m} = 0,0175\,\mathrm{\frac{\Omega \cdot mm^2}{m}}\]

Es könnte sich um Kupfer handeln!

Es gibt auch Halbleiter-DMS. Bei diesen Materialien ist die Änderung des spezifischen Widerstands nicht mehr zu vernachlässigen, da er sich aufgrund des piezoresistiven Effekts sehr stark ändert. P-dotiertes Silizium weist beispielsweise ein \(k\) von bis zu 190 auf, n-dotiertes Silizium sinkt den \(k\)-Faktor auf - 100 ab. Das heißt, dass der Widerstandswert mit zunehmender Dehnung kleiner wird! Halbleiter-DMS haben also einen höheren \(k\)-Faktor, jedoch auch eine höhere Temperaturabhängigkeit, weshalb immer Temperaturkompensationssysteme miteingebraucht werden müssen. Für Präzisionsmessungen benötigt man eine solche Temperaturkompensation allerdings auch bei Metall-DMSs. Außerdem können Metall-DMSs um das 10-fache mehr Dehnung aufnehmen.
Eine eleganten Zusammensatzung wäre ein n- und p-dotierter Silizium-DMS mit jeweils dem gleichen, aber entgegengesetzten \(k\)-Faktor, welche in einer Messbrücke zusammengeschaltet werden [Bot].

Biegungsbeanspruchung#

Es gibt verschiedene Möglicheiten DMS zur Kraftmessung zu nutzen. Die Sensoren können beispielsweise an einen Biegebalken angebracht werden, wie es in Abb. 111 dargestellt ist, wodurch man die Biegung des Körpers messen kann.

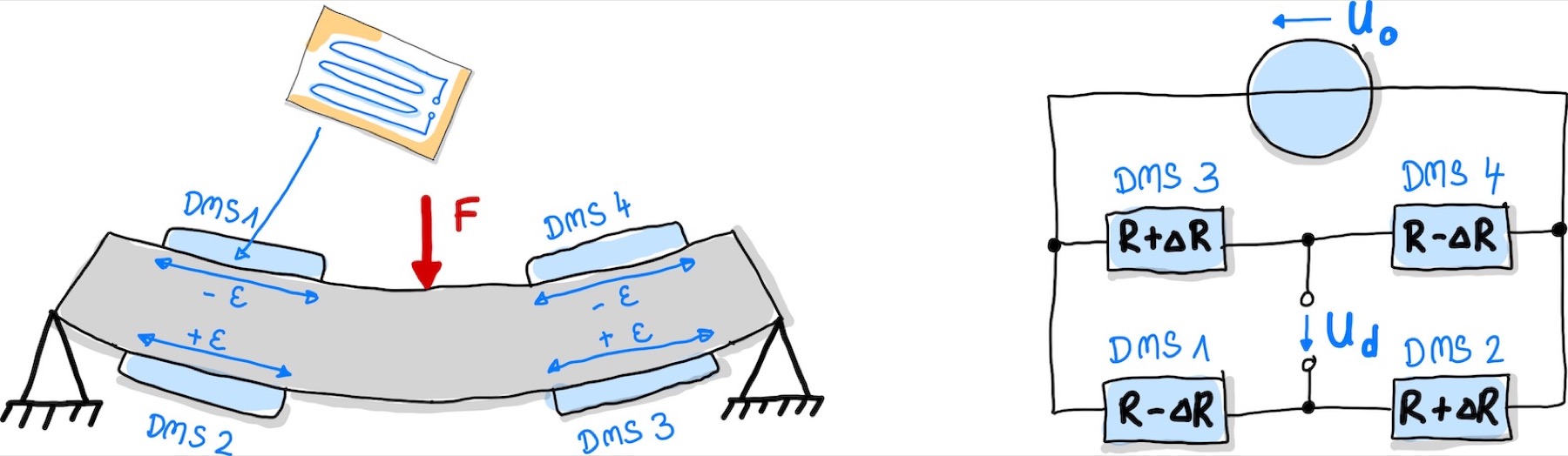
dms_bieg_mess

Abb. 111 DMSs sind an einem Biegebalken angebracht und können so die Wölbung messen.#

Erfährt der Balken eine Kraft von außen, aufgrund derer er sich zu verformen beginnt, kann die resultierende Wölbung an den Oberflächen mittels DMS gemessen werden. Hierbei sieht der DMS oben eine Stauchung und der DMS auf der Unterseite (gegenüber der Krafteinwirkung) eine Streckung.

Die vier DMSs können direkt mittels einer Vollbrücke ausgelesen werden. Die Vorzeichen von zwei DMSs sind jeweils entgegengesetzt, da sie entweder gestaucht oder gestreckt werden. Somit lässt sich das Differentialprinzip auf die Messung hier übertragen. Die Diagonalspannung in der Messbrücke und somit die Kennlinie des Messsystems lautet:

\[U_d = U_0 \cdot \frac{\Delta R}{R} = U_0 \cdot k \cdot \epsilon\]

Typischerweise können Kräfte von 1-50 kN gemessen werden [Par].

Zug und Druck#

Zug und Druck können mit der Anordnung von DMSs gemessen werden, wie es in Abb. 112 dargestellt ist.

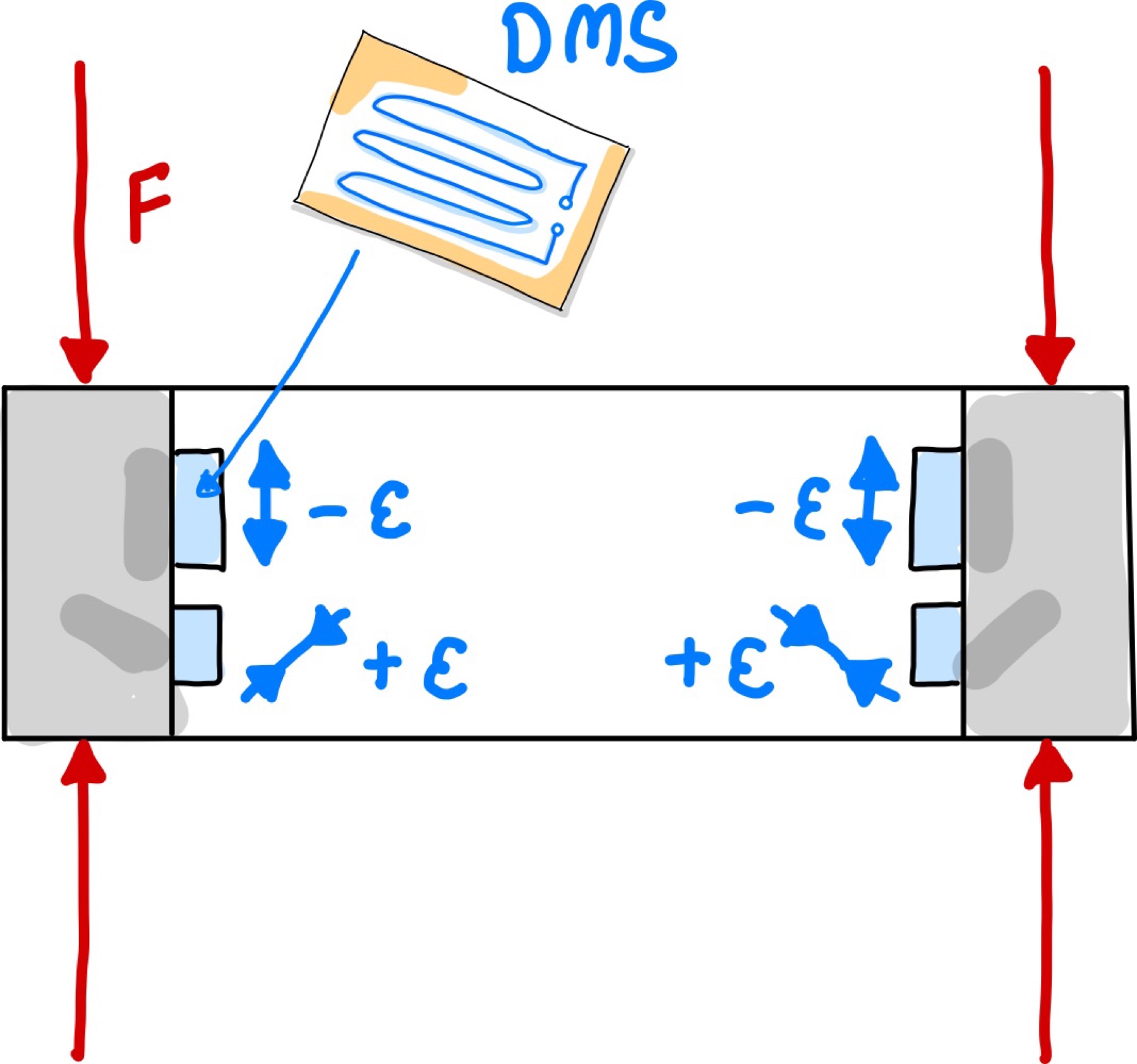
dms_druck

Abb. 112 DMSs sind innen in einem Hohlkörper angebracht an der Innenwand angebracht und können so die Zug- und Druckkräfte an der Zylinderwand zu messen.#

Auch hierfür werden die DMS wieder innenliegend an den Hohlkörper angebracht. Werden die DMS entlang der Kraftrichtung angebracht, so werden sie längs ihrer Anbringungsrichtung gedehnt und gestaucht. Sie können jedoch auch quer zur Krafteinwirkungsrichtung installiert werden, wodurch sie dann genau entgegengesetzt gestaucht bzw. gedehnt werden. Es können Kräfte zwischen 20 kN bis einige MN gemessen werden [Bot].

Scherkräftemessung#

Hat man in einem Festkörper beispielsweise zwei Hohlräume oder Bohrungen, können in diesen DMSs eingebracht werden um Scherkräfte innerhalb der Körper zu messen. Dies ist in Abb. 113 dargestellt.

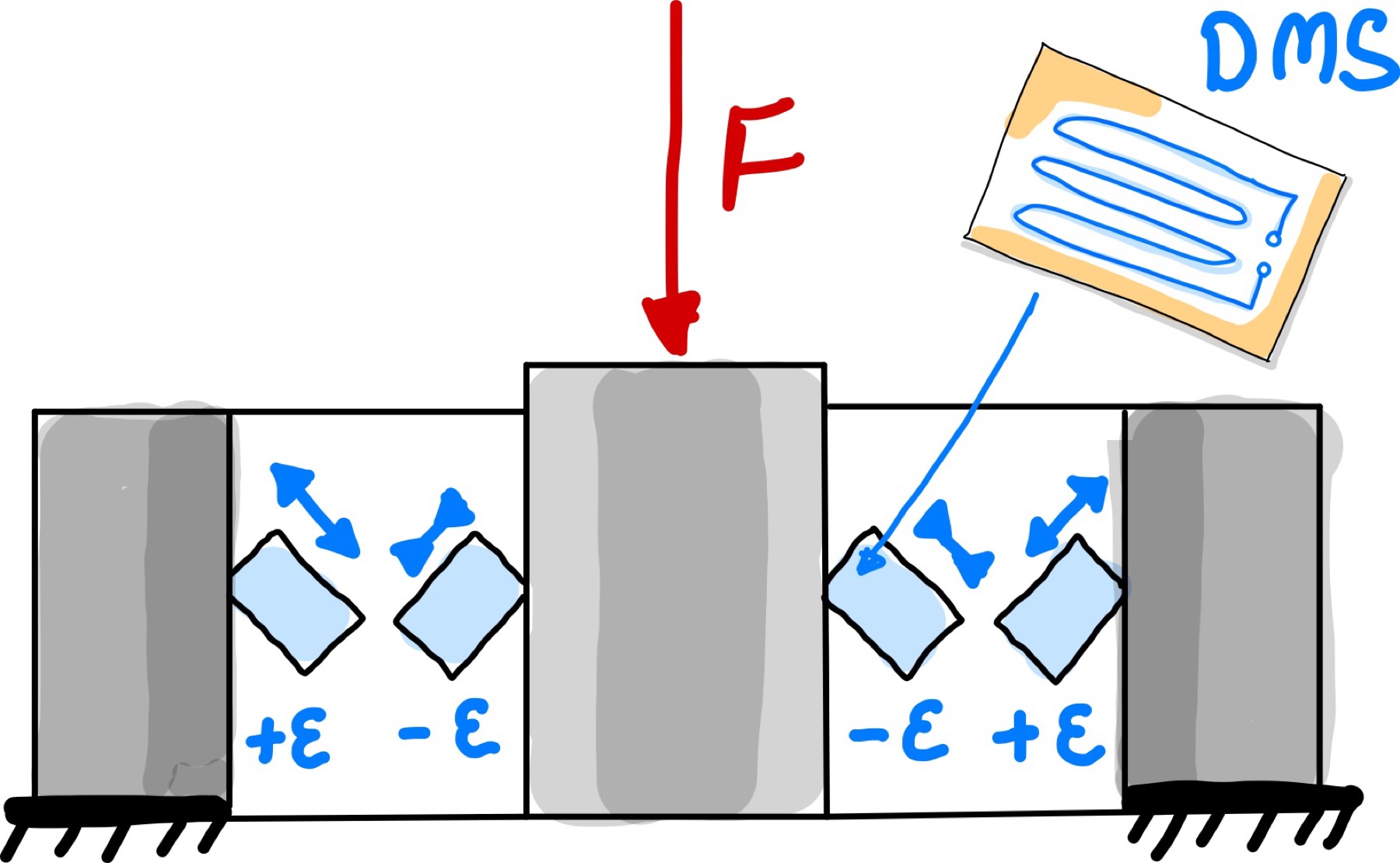
dms_scher

Abb. 113 DMSs sind innen an der Innenwand von zwei Bohrungen angebracht um Scherkräfte zu messen.#

Die Scherkräfte werden gemessen indem die DMS in einem 45° Winkel an die Rand geklebt werden. Nutzt man weitere Sensoren mit einem -45° Winkel so können wieder 4 Sensoren mittels einer Vollbrücke ausgelesen werden. Hierbei können Kräfte im Bereich von 20kN bis einigen MN gemessen werden [Bot].

Temperaturkompensation#

Wie oben erwähnt sind für Präzisionsmessungen Temperaturkompensationen notwendig. Hierfür kann ein zweiter, baugleicher DMS an die Messbrücke mitangeschlossen werden, der jedoch so installiert ist, dass er keine Dehnung erfährt. Er steht lediglich in thermischen Kontakt mit dem zu messenden Körper und liefert eine Referenzmessung für die Temperaturabhängigkeit der DMS-Messung.

Referenzen#

[Bot] (1,2,3)

missing year in boettcher2020

[Par] (1,2)

missing year in parthier2020