Laserinterferometrie

Als Interferometer bezeichnet man ein Messsystem, indem zwei Wellen miteinander so überlagert werden, dass sie miteinander interferieren. Die Wellen tragen Informationen der zu messenden Größe, typischerweise in der Phase der Welle, welche durch verschiedenste Methoden weiter verarbeitet werden kann.

Prinzipiell kann Interferenz bei jeder Art von Welle auftreten, egal ob Licht-, Schall-, Materie- oder Wasserwelle. Wir wollen ins in diesem Kapitel auf die Laserinterferometer, also optische Interferometrie, konzentrieren.

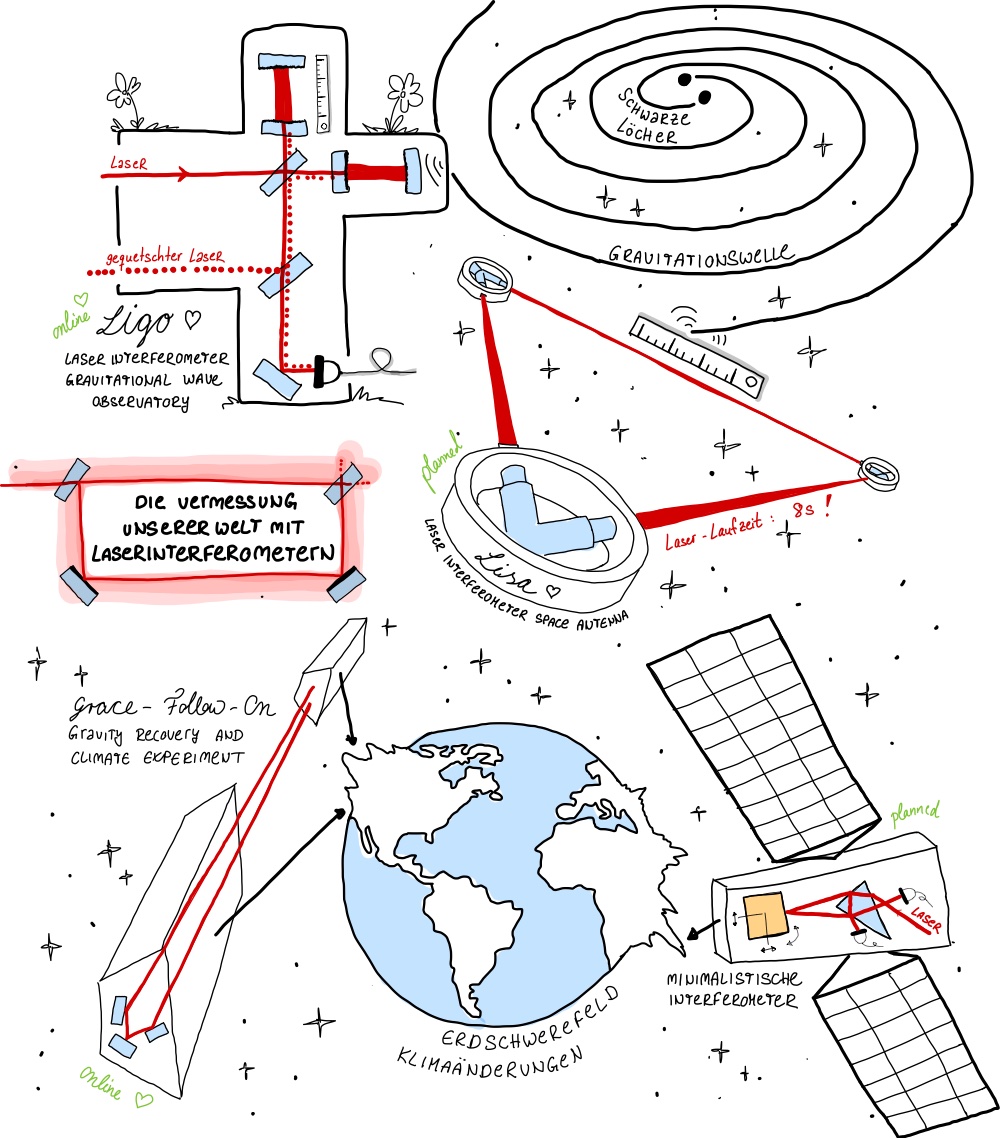
Abb. 129 Die Vermessung von Gravitation mittels Laserinterferometrie. Ein Überblick ausgewählter Missionen.

Interferometer

Interferometer eignen sich insbesondere für Hochpräzisionsmessungen. Das Funktionsprinzip ist immer ähnlich: Zwei Lichtstrahlen werden durch Optiken (Spiegel) und halbdurchlässige Spiegel auf verschiedene Bahnen gelenkt. Wichtig ist es, die beiden Lichtstrahlen an einem halbdurchlässigen Spiegel möglichst perfekt am Ende zu überlagern (interferieren), sodass ein Interferenzmuster am Ausgang des Interferometers entsteht. Dadurch werden die beiden interferierten Lichtstrahlen miteinander verglichen. Ändert sich die Phase eines Lichtstrahls, so ändert sich das Interferenzmuster. D.h. das Muster hängt von der optischen Weglänge ab, die die jeweiligen Lichtstrahlen bis zur Interferenz zurückgelegt haben. Dadurch können differentielle Weglängenunterschiede zwischen den zwei Interferometerarmen gemessen werden, was für folgende Anwendungen benutzt werden kann:

• Positionsänderungen

• Brechungsindex oder Dichteänderungen in einem der beiden Wege

• Winkelmessungen

• Spektroskopie

• Vibrationsmessungen

• Geschwindigkeit- und Beschleunigungsmessung (siehe Radar)

• Verformungsmessung

• FTIR-Spektrometrie (chemische Analysen)

• Gravitationswellendetektion

Kennt man die Wellenlänge \(\lambda\) des verwendeten Laserlichts, also z.B. 1550nm (die entspricht der Telekommunikationswellenlänge), so kann man die optische Phase in eine Längenänderung konvertieren.

\[ 2 \cdot \Delta L = \left( \frac{\Delta \phi}{2\pi} \right) \cdot \lambda \]

• \(\Delta L\) ist die Weglängendifferenz,

• \( \Delta \phi\) ist die Phasenverschiebung in Radiant,

• \( \lambda \) ist die Wellenlänge des Lichts.

Der Faktor 2 resultiert daraus, dass in Interferometern der Laserstrahl reflektiert wird und somit die Weglängendifferenz 2x durchläuft. Dies erhöht die Auflösung der Messung um den Faktor 2.

• Je kleiner die Wellenlänge, desto genauer können Positiosänderungen des Spiegels gemessen werden

• Allerdings müssen bei höheren Dynamiken, also Bewegungen die eine Wellenlänge überschreiten, die Wechsel von Hell- nach Dunkel gezählt werden, wobei Fehler passieren können. Daher eignen sich homodyne Laserinterferometer nur bedingt zur Messung von größeren Veränderungen

• Absolute Längenmessungen sind nicht möglich, lediglich relative Positionsänderungen von Objekten, da sich die Kennlinie periodisch wiederholt. Dies nennt man auch Inkrementalgeber.

Signal eines homodynen Laserinterferometers

Bei homodyner Laserinterferometrie werden zwei Lichtstrahlen mit der exakt gleichen Wellenlänge bzw. Frequenz überlagert. Die jeweiligen elektromagnetischen Felder in den beiden Interferometerarmen können wiefolgt aufgeschrieben werden:

\[E_1 = A_1 \cos(\omega_0 t)\]

und

\[E_2 = A_2 \cos(\omega_0 t + \varphi)\]

wobei wir die Amplitude mit \(A\) bezeichnen und \(\omega_0\) die Laserfrequenz ist (im Bereichen von einigen Hundert THz). Weiterhin nehmen wir an, dass der Interferometerarm 1 seine Länge nicht ändert und wir im 2. Laserarm die Phase \(\varphi\) messen, die die zu messende Information beinhaltet (z.B. die Bewegung eines Spiegels).

Diese beiden Strahlen werden an einem halbdurchlässigen Spiegel miteinander überlagert. Deren Leistung wird mittels einer Photodiode gemessen, die die einfallene Strahlungsleistung in einen Photostrom umwandelt. Die eintreffende Intensität lässt sich wiefolgt aus den beiden elektromagnetischen Feldern berechnen:

(2)\[\begin{align} I &\propto |E_1 + E_2|^2 = |A_1 \cos(\omega_0 t) + A_2 \cos(\omega_0 t + \varphi)|^2 \\ &= A_1^2 \cos(\omega_0 t)^2 + 2 A_1 A_2 \cos(\omega_0 t) \cos(\omega_0 t + \varphi) + A_2^2 \cos(\omega_0 t + \varphi)^2 \end{align}\]

Mittels Additionstheoremen

(3)\[\begin{align} \cos^2x &= \frac{1}{2}\left(1+ \cos(2x) \right) \\ \cos x \cos y &= \frac{1}{2}\left(\cos(x-y) + \cos(x+y) \right) \end{align}\]

lässt sich die Gleichung weiter umschreiben zu:

(4)\[\begin{align} I &\propto \frac{A_1^2}{2} + \frac{A_1^2}{2}\cos(2\omega_0 t) + A_1 A_2 \left( \cos(-\varphi) + \cos(2\omega_0 t + \varphi) \right) + \frac{A_2^2}{2} + \frac{A_2^2}{2}\cos(2\omega_0 t + 2 \varphi) \end{align}\]

Da es sich bei der Laserfrequenz um eine sehr hoch frequente Schwingung handelt, die bist zu \(10^14\) mal pro Sekunde oszilliert (z.B. 280 THz für infrarotes Licht), agiert die Photodiode selbst als Tiefpassfilter, da sie so hohe Frequenzen nicht mehr auflösen kann. Daher können wir im Folgenden alle Cosinus-Terme der Frequenz \(2\omega_0\) vernachlässigen:

(5)\[\begin{align} I &\propto \frac{A_1^2}{2} + A_1 A_2 \left( \cos(-\varphi) \right) + \frac{A_2^2}{2} \\ &= \frac{A_1^2}{2} + \frac{A_2^2}{2} + A_1 A_2 \cos(-\varphi) \end{align}\]

Die Intensität, bzw. Leistung auf der Photodiode hängt somit also nur noch von einem DC-Term ab, der nicht oszilliert, von der Phase \(\varphi\) die es zu messen gilt und dem Produkt der zwei Amplituden. Der DC-Term entspricht dem Gleichanteil des Cosinus-Signals und kann ebenfalls rausgefiltert werden, sodass lediglich das Cosinus-Signal mit der relevanten Phaseninformation übrig bleibt:

\[I \propto A_1 A_2 \cos(\varphi)\]

Dies ist die periodische Kennlinie eines homodynen Laserinterferometers und wird im Folgenden grafisch dargestellt. Das animierte Oszilloskop-Signal zeigt an, wie sich die Ausgangsleistung in einem Interferometer je nach Spiegelposition ändern würde.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
import warnings
warnings.filterwarnings('ignore')
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
plt.rcParams['font.size'] = 10; # Schriftgröße
fig, ax = plt.subplots(1,2,figsize=(7,3))

A_1 = 1.0
A_2 = 1.0
phase = np.linspace(0, 4*np.pi, num=10000)
ax[0].set_ylabel('Photostrom (a.u.)')
ax[0].set_xlabel('Phase (rad)')
ax[0].set_xticks([0, np.pi, 2*np.pi, 3*np.pi, 4*np.pi], ['0', r'$\pi$', r'$2\pi$', r'$3\pi$', r'$4\pi$'])
ax2 = ax[0].twiny()
ax2.set_xticks([0, np.pi, 2*np.pi, 3*np.pi, 4*np.pi], ['0', r'', r'775', r'', r'1550'])
ax2.set_xlabel('Spiegelposition (nm)')
ax[0].set_ylim(-1.1,1.1)

t = np.linspace(0, 1, num=10000)

ax[1].set_ylabel('Photostrom (a.u.)')
ax[1].set_xlabel('Zeit (s)')
ax[1].set_ylim(-1.1,1.1)
ax[1].set_title('Oszilloskop: ')

num = 51
tTM = np.linspace(0,2*np.pi , num=num)
xTM = np.cos(tTM)

line, = ax[0].plot(phase, A_1 * A_2 * np.sin(phase), color='tab:blue')
linet, = ax[1].plot(t, A_1 * A_2 * np.sin(0*phase), color = 'tab:red')


def animate(i):
    line.set_ydata(A_1 * A_2 * np.sin(phase + xTM[i]))  # update the data.
    linet.set_ydata(A_1 * A_2 * np.sin(0*phase + xTM[i]))  # update the data.
    return line, linet,


ani = animation.FuncAnimation(
    fig, animate, interval=20, blit=True, save_count=num)



# To save the animation, use e.g.
#
# ani.save("movie.mp4")
#
# or
#
# writer = animation.FFMpegWriter(
#     fps=15, metadata=dict(artist='Me'), bitrate=1800)
# ani.save("movie.mp4", writer=writer)
plt.tight_layout()
plt.close()
HTML(ani.to_jshtml())

Once Loop Reflect

Signal eines heterodynen Laserinterferometers

Um auch dynamische Bewegungen von Objekten zu messen, die das Ausmaß einer Wellenlänge überschreiten, werden häufig heterodyne Laserinterferometer benutzt. Hierbei müssen zwar keine Ringe mehr gezählt werden, doch die Auslesung eines solchen Interferometers ist etwas komplizierter als nur den Intensitäts- bzw. Leistungsschwankungen auf einer Photodiode zu folgen, wie es bei homodynen Laserinterferometern praktiziert wird.

In einem heterodynen Laserinterferometer überlagert man zwei elektromagnetische Wellen unterschiedlicher Frequenz:

\[E_1 = A_1 \cos(\omega_1 t)\]

und

\[E_2 = A_2 \cos(\omega_2 t + \varphi)\]

Wir nehmen wieder der Einfachheithalber an, dass der eine Interferometerarm stabil ist und sich lediglich die Phasenlage im zweiten Interferometerarm mit \(\varphi\) ändert. Wieder berechnen wir die Intensität auf der Photodiode mittels:

(6)\[\begin{align} I &\propto |E_1 + E_2|^2 = |A_1 \cos(\omega_1 t) + A_2 \cos(\omega_2 t + \varphi)|^2 \\ &= A_1^2 \cos(\omega_1 t)^2 + 2 A_1 A_2 \cos(\omega_1 t) \cos(\omega_2 t + \varphi) + A_2^2 \cos(\omega_2 t + \varphi)^2 \end{align}\]

und wieder können wir die Gleichung mittels Additionstheoremen von oben vereinfachen zu:

(7)\[\begin{align} I &\propto \frac{A_1^2}{2} + \frac{A_1^2}{2}\cos([\omega_1+\omega_2] t) \\ &+ A_1 A_2 \left( \cos([\omega_1-\omega_2]t-\varphi) + \cos([\omega_1+\omega_2] t + \varphi) \right) \\ & + \frac{A_2^2}{2} + \frac{A_2^2}{2}\cos([\omega_1+\omega_2] t + 2 \varphi) \end{align}\]

Wieder können wir annehmen, dass hohe Frequenzanteile aufgrund der Tiefpassverhaltens der Photodiode nicht mehr aufgenommen werden und wir können die Terme mit \(\omega_1 + \omega_2\) vernachlässigen:

(8)\[\begin{align} I &\propto \frac{A_1^2}{2} + A_1 A_2 \cos([\omega_1-\omega_2]t-\varphi) + \frac{A_2^2}{2} \\ &= \frac{A_1^2}{2} + \frac{A_2^2}{2} + A_1 A_2 \cos([\omega_1-\omega_2]t-\varphi) \end{align}\]

Der DC-Offset enthält wieder keine physikalischen Informationen und kann ebenfalls gefiltert werden. Übrig bleibt ein Photostrom, der nun mit einer Frequenz oszilliert, die genau. derDifferenzfrequenz der beiden interferierten Laserstrahlen entspricht, und die heterodyne Frequenz oder auch Schwebung genannt wird:

\[I \propto A_1 A_2 \cos(\omega_\mathrm{het}t-\varphi)\]

Im Folgenden stellen wir diese Kennlinie wieder grafisch dar. Hierbei ist jetzt zu beachten, dass die Schwingung nicht gegenüber der Phasenlage gezeichnet wird, sondern gegenüber der Zeit. Das physikalische Signal steckt weiterhin in der Phase und muss mit spezieller Auswerteelektronik von der Schwebungsfrequenz extrahiert werden, was wir uns gleich genauer ansehen werden.

Die Differenzfrequenz (Schwebung) ist:

\[\omega_\mathrm{het} = \omega_1 -\omega_2\]

Praktisch gesehen kann diese zwischen den beiden Lasern verändert werden, indem die Laserfrequent eines Lasers leicht geschoben wird. Dadurch kann sie auf die Bandbreite der Photodiode und Ausleseelektronik angepasst werden. Die Phase liefert wieder die Information über die Spiegelposition. Ändert sich die Phase, wie es im rechten Diagramm dargestellt ist, wandert die Cosinus-Kurve nach links oder rechts, je nach Vorzeichen der Phasenänderung, wie es in der nachfolgenden Animation dargestellt ist:

\[\varphi = \frac{2 \pi}{\lambda}\]

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
plt.rcParams['font.size'] = 10; # Schriftgröße

fig, ax = plt.subplots(figsize=(5,3))

A_1 = 1.0
A_2 = 1.0
f_het = 10e3
phase = 0
t = np.linspace(0, 0.5e-3, num=10000)

x = np.arange(0, 2*np.pi, 0.01)
line, = ax.plot(t*1e3, A_1 * A_2 * np.sin(2*np.pi*f_het * t), color='tab:red')
ax.set_xlabel('Zeit (ms)')
ax.set_ylabel('Photostrom (a.u.)')
ax.set_title('Oszilloskop: ')
num = 51
tTM = np.linspace(0,2*np.pi , num=num)
xTM = np.cos(tTM)

def animate(i):
    line.set_ydata(A_1 * A_2 * np.sin(2*np.pi*f_het * t + xTM[i]))  # update the data.
    return line,


ani = animation.FuncAnimation(
    fig, animate, interval=40, blit=True, save_count=num)

# To save the animation, use e.g.
#
# ani.save("movie.mp4")
#
# or
#
# writer = animation.FFMpegWriter(
#     fps=15, metadata=dict(artist='Me'), bitrate=1800)
# ani.save("movie.mp4", writer=writer)
plt.tight_layout()
plt.close()
HTML(ani.to_jshtml())

Once Loop Reflect

Um an die physikalische Information, die Positionsänderung des Objektes, zu kommen, muss also die Phase einer Schwingung ausgelesen werden. Hierfür eignen sich im Prinzip zwei Methoden, die je nach Anwedungsbereich und der zu erwartenden Dynamik des Signals, benutzt werden.

Phasenauslesung

Die IQ-Demodulation, oder auch I&Q-Verfahren (In-Phase-&-Quadrature-Verfahren), bietet die Möglichkeit die Phaseninformation \(\varphi(t) = \varphi\) aus einem hochfrequenten Trägersignal zu erhalten, z.B. von

\[A(t) = A_0 \cos(\omega_\mathrm{het}t-\varphi)\]

Dies kann sowohl die Phasenlage eines Interferometers auslesen, wir aber auch in der Radartechnik benutzt.

Das gemessene Signal \(A(t)\) wird analog oder digital in zwei Wege aufgeteilt und in jedem demoduliert indem es mit einer Oszillatorfrequenz, die der Signalfrequenz \(\omega_\mathrm{het}\) entspricht, gemischt wird:

• Im ersten Weg wird die Demodulation mit der originalen Phasenlage (in-phase) durchgeführt und man erhält die I-Quadratur:

(9)\[\begin{align} I &= A(t) \cdot \cos(\omega_\mathrm{het}t) \\ &= A_0 \cos(\omega_\mathrm{het}t-\varphi) \cdot \cos(\omega_\mathrm{het}t) \\ &= \frac{A_0}{2} \cdot \left( \cos(-\varphi) + \cos(2\omega_\mathrm{het}t-\varphi) \right) \\ &= \frac{A_0}{2} \cdot \cos(\varphi) \end{align}\]

• Der zweite Weg wird mit Referenzfrequenz demoduliert, die um 90° gegenüber dem ersten Weg verschoben ist, was die Q-Quadratur ergibt:

(10)\[\begin{align} Q &= A(t) \cdot \sin(\omega_\mathrm{het}t) \\ &= A_0 \cos(\omega_\mathrm{het}t-\varphi) \cdot \sin(\omega_\mathrm{het}t) \\ &= \frac{A_0}{2} \cdot \left( \sin(\varphi) + \sin(2\omega_\mathrm{het}t-\varphi) \right) \\ &= \frac{A_0}{2} \cdot \sin(\varphi) \end{align}\]

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib.patches import ConnectionPatch

fig, (axl, axr) = plt.subplots(
    ncols=2,
    sharey=True,
    figsize=(6, 2),
    gridspec_kw=dict(width_ratios=[1, 3], wspace=0),
)
axl.set_aspect(1)
axr.set_box_aspect(1 / 3)
axr.yaxis.set_visible(False)
axr.xaxis.set_ticks([0, np.pi, 2 * np.pi], ["0", r"$\pi$", r"$2\pi$"])
axl.set_xlabel('I-Quadratur')
axl.set_ylabel('Q-Quadratur')
axl.xaxis.set_ticks([])
axl.yaxis.set_ticks([])
# draw circle with initial point in left Axes
x = np.linspace(0, 2 * np.pi, 50)
axl.plot(np.cos(x), np.sin(x), "k", lw=0.3)
point, = axl.plot(0, 0, "o")

# draw full curve to set view limits in right Axes
sine, = axr.plot(x, np.sin(x))

# draw connecting line between both graphs
con = ConnectionPatch(
    (1, 0),
    (0, 0),
    "data",
    "data",
    axesA=axl,
    axesB=axr,
    color="C0",
    ls="dotted",
)
fig.add_artist(con)


def animate(i):
    pos = np.cos(i), np.sin(i)
    point.set_data(*pos)
    x = np.linspace(0, i, int(i * 25 / np.pi))
    sine.set_data(x, np.sin(x))
    con.xy1 = pos
    con.xy2 = i, pos[1]
    return point, sine, con


ani = animation.FuncAnimation(
    fig,
    animate,
    interval=50,
    blit=False,  # blitting can't be used with Figure artists
    frames=x,
    repeat_delay=100,
)
plt.tight_layout()
plt.close()
HTML(ani.to_jshtml())

Once Loop Reflect

Die Phaseninformation erhält man über die Rückrechnung der Quadraturen:

\[\varphi = \arctan\left(\frac{Q}{I}\right) = \arctan\left(\frac{A_0/2 \sin(\varphi)}{A_0/2 \cos(\varphi)}\right) = \arctan\left(\frac{\sin(\varphi)}{\cos(\varphi)}\right) = \arctan(\tan(\varphi)) = \varphi\]

Die Amplitude des Signal kann ebenfalls aus den Quadraturen berechnet werden:

\[A = \sqrt{I^2 + Q^2} = \sqrt{\frac{A_0^2}{4} \cos^2(\varphi) + \frac{A_0^2}{4} \sin^2(\varphi)} = \sqrt{\frac{A_0^2}{4} (\cos^2(\varphi) + \sin^2(\varphi))} = \frac{A_0}{2}\]

Phasenregelschleife

Die zweite, etwas robustere Methode für höhere Dynamiken, ist die Phasenregelschleife. Hierbei wird in einem Regelkreis die Phase des Referenz-Oszillators dem einkommenden Signal entsprechend nachgesteuert. Dadurch kann auch Frequenzänderungen oder großen Phasenänderungen gefolgt werden, da die Oszillatorfrequenz (bzw. -phase) intern nachgesteuer wird. Im Prinzip werden hierfür vier Schritte benötigt:

1. Die Phasenlage zwischen Messsignal und Referenz-Signal (Oszillator) wird mittels einem Phasenvergleicher bestimmt (z.B. über IQ-Demodulation).

2. Ein Aktor/Regler, der ein Steuersignal in Abhängigkeit von der zuvor gemessenen Phasenlage ausgibt. Diese Komponente nennt sich auch Schleifenfilter und weist das Verhalten eines Tiefpassfilters mit relativ hoher Eckfrequenz auf. Häufig handelt es sich hierbei um einen PI (Proportional-Integral) Regler

3. Ein regelbarer Oszillator, dem das Steuersignal zugeführt wird und dadurch dem einkommenden Signal hinterher läuft.

4. Ein Frequenzteiler, der die Ausgangsphase/-frequenz an den Phasenvergleicher unter Punkt 1.) zurück gibt und die Regelschleife gilt. Der andere Ausgangs des Frequenzteilers ist liefert das gewünschte Messsignal.

Eine Phasenregelschleife (kurz PLL = phase-locked loop) kann sowohl mittels analogen als auch digitalen Komponenten implementiert werden. Die digitale Variante nennt sich dann DPLL.

Optischen Resonatoren

Die Empfindlichkeit von Interferometern kann durch den Einsatz von optischen Resonatoren stark verbessert werden. Mittels zusätzlichen Spiegeln werden die Anzahl der Reflektionen für die Längenmessung zusätzlich erhöhen. Die optischen Resonatoren “speichern” das Licht, indem sie es zwischen zwei Spiegeln hin und her reflektieren, wodurch die effektive Weglänge des Lichts verlängert wird. Dies erhöht die Empfindlichkeit des Interferometers für Messungen der Längenänderung.

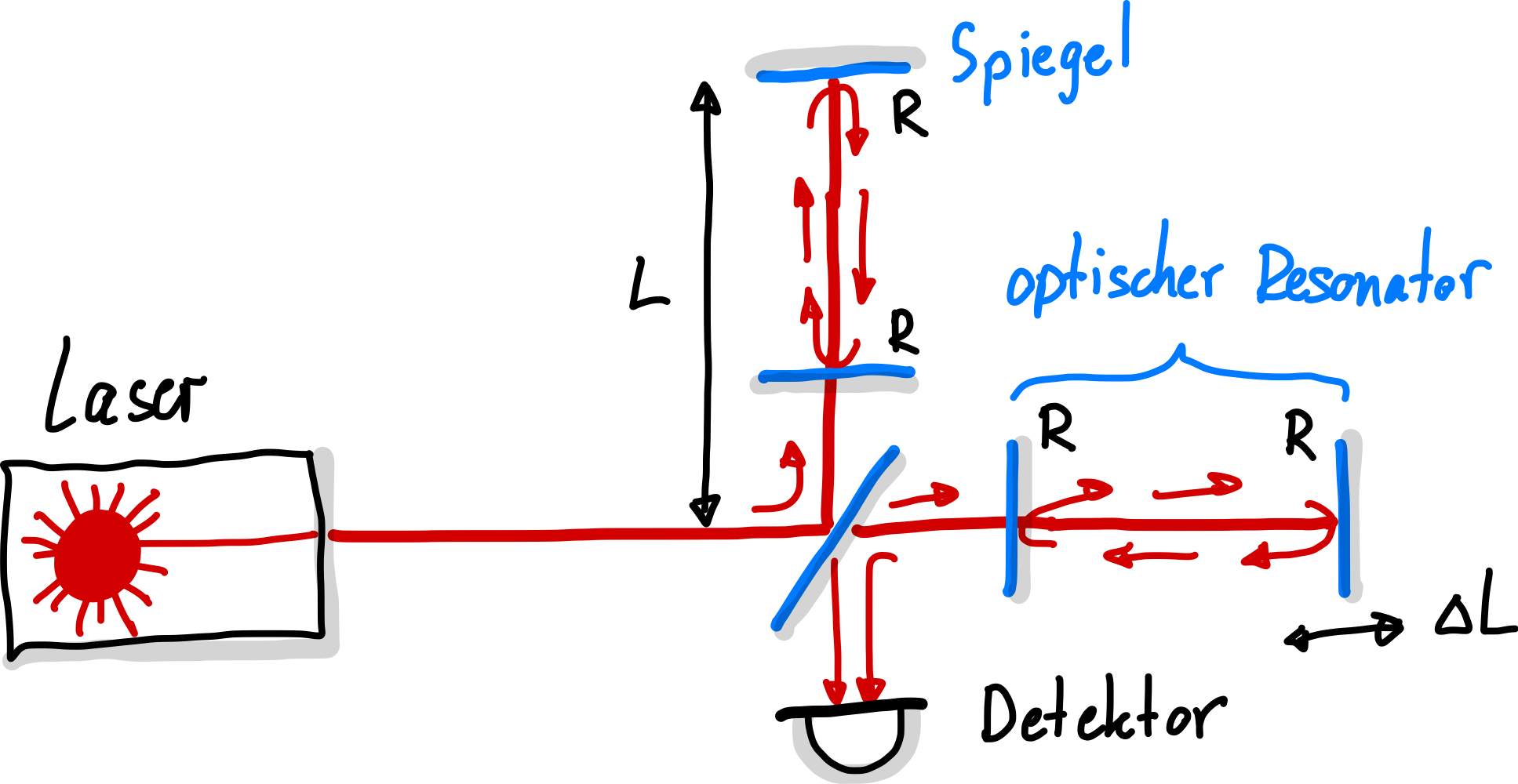
Abb. 130 Laserinterferometer mit optischen Resonator.

Der Einfluss der Phasenänderung auf die Intensität kann durch die Finesse des Resonators und die Eigenschaften des verwendeten Lichts beeinflusst werden. Die Grundgleichung für die Intensität der Lichtwelle in einem Fabry-Perot-Resonator (eine Art von optischem Resonator) in Abhängigkeit von der Phasenänderung ist:

\[ I(\Delta\phi) = I_0 \cdot \frac{1}{1 + F \cdot \sin^2(\Delta\phi/2)} \]

wo:

• \(I(\phi)\) ist die Intensität des Lichts im Resonator,

• \(I_0\) ist die Intensität des einfallenden Lichts,

• \(\mathcal F\) ist die Finesse des Resonators,

• \(\Delta\phi\) ist die Phasenänderung.

In dieser Gleichung ist die Finesse (\(\mathcal F\)) ein Maß für die “Schärfe” der Resonanz des Resonators und wird oft durch die Formel

\[ \mathcal F = \frac{\pi \sqrt{R}}{1 - R} \]

ausgedrückt, wobei \(R\) die Reflektivität der Spiegel ist.

Die Gleichung zeigt, dass die Intensität im Resonator maximiert wird, wenn die Phasenänderung ein Vielfaches von \(2\pi\) ist, was bedeutet, dass die Bedingungen für konstruktive Interferenz erfüllt sind. Umgekehrt wird die Intensität minimiert, wenn die Phasenänderung ein ungerades Vielfaches von \(\pi\) ist, was die Bedingungen für destruktive Interferenz erfüllt.

Die Breite der Resonanzspitzen und die Tiefe der Resonanztäler werden durch die Finesse des Resonators beeinflusst. Ein Resonator mit hoher Finesse wird schmalere Resonanzspitzen und tiefere Resonanztäler aufweisen, d.h. die Kennlinie wird steiler, was einer höheren Empfindlichkeit entspricht.

Eine kleine Bewegung der Spiegel kann nun eine drastische Änderung in der Intensität verursachen, was die Messung von sehr kleinen Signalen, wie den von Gravitationswellen verursachten, ermöglicht. Im nachfolgenden Diagramm ist dargestellt, wie sich die Kennlinie in der Anwesenheit von optischen Resonatoren in Abhängigkeit von der Spiegelreflektivität \(R\) in einem Interferometer ändert.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML
plt.rcParams['font.size'] = 10; # Schriftgröße


# Initialize the figure and axis
fig, ax = plt.subplots(figsize=(5, 3), tight_layout=True)


# Funktion zur Berechnung der Intensität in Abhängigkeit von der Phasenverschiebung
def calculate_intensity(reflectivity, phase_difference):
    finesse = np.pi * reflectivity / (1 - reflectivity)
    intensity = 1 / (1 + finesse * np.sin(phase_difference / 2.0)**2)
    return intensity

# Funktion zum Aktualisieren der Grafik
def update(reflectivity):
    x = np.linspace(0, 6 * np.pi, 1000)  # Phasenverschiebung von 0 bis 6*pi
    phase_difference = x
    intensity = calculate_intensity(reflectivity, phase_difference)
    
    ax.plot(phase_difference, calculate_intensity(0.9, phase_difference), color='tab:blue', lw=4, alpha=0.5, label='Resonator Reflektivität: R = 0.9')
    ax.plot(phase_difference, intensity, color='tab:red', label='Resonator Reflektivität: R =%5.2f'%(reflectivity))
    # Set plot labels and legend
    #ax.set_title('Analog zeitdiskret: Abgetastete Sinuswelle')
    ax.set_xlabel('Phasenverschiebung (rad)')
    ax.set_ylabel('Intensität')
    ax.set_ylim([0, 1])
    ax.grid(True)
    ax.legend(loc='upper right')


# Funktion zur Aktualisierung der Animation
def animate(reflectivity):
    ax.clear()
    update(reflectivity)

# Create an animation by varying reflectivity from 0.01 to 0.99 with a step of 0.01
ani = FuncAnimation(fig, animate, frames=np.arange(0.01, 0.999, 0.01), repeat=False)

# Anzeigen der Animation
#plt.tight_layout()
plt.close()
HTML(ani.to_jshtml())

Once Loop Reflect

Die Empfindlichkeit kann durch optische Resonatoren extrem gesteigert werden, jedoch wird der Messbereich dadurch verkleinert und das System selber darf sich kaum noch bewegen.