Messtechnik in Dunkle Materie Experimenten#
Einleitung#
Das Geheimnis der Dunklen Materie ist eine der größten Herausforderungen in der Astrophysik. Ihre Existenz wird postuliert, um Phänomene wie die unerwartet hohen Rotationsgeschwindigkeiten von Galaxien zu erklären. Die sichtbare Materie reicht nicht aus, um diese hohen Geschwindigkeiten zu erreichen. Dunkle Materie hingehen wäre nicht sichtbar, würde aber trotzdem einen gravitativen Einfluss auf die Galaxie ausüben und könnte die Rotation dadurch beschleunigen. Ein weiteres Indiz für Dunkle Materie ist die auffällige Transparenz des Universums für Strahlung mit Energien im Bereich von TeV. Eine Theorie besagt, dass Strahlung sich auf ihrem Weg durch das Universum in Dunkle Materie umwandeln könnte, welche nicht wechselwirkt und somit lange Strecken zurück legen kann. Zu einem späteren Zeitpunkt verwandelt sich diese Dunkle Materie zurück in Strahlung und es hast den Eindruck, als wäre das Universum unglaublich transparent für diese Strahlung. Dieser Umwandlungsprozess geschieht nur in der Anwesenheit von starken Magnetfeldern, wie zum Beispiel extragalaktischen Magnetfeldern in unserem Universum. Wir können diesen Prozess aber auch künstlich im Labor herstellen und damit Dunkle Materie in Licht (Strahlung) verwandeln und sichtbar machen. Genaus können wir im Labor auch aus Licht Dunkle Materie herstellen. Beides wird in Hamburg, 30m unter der Erde, am DESY im ALPS II Experiment gemacht. Hierbei handelt es sich um so genannten Axion-artige Teilchen, die, wie oben beschrieben, ein heißer Kandidat für Dunkle Materie sind.
ALPS II Experiment#
Das ALPS II Experiment am DESY verfolgt das Ziel, Axion-ähnliche Teilchen im Labor zu produzieren und zu messen. ALPS II, kurz für “Any Light Particle Search II”, nutzt den oben beschriebenen Effekt der Umwandlung von Axion-ähnlichen Teilchen in Licht und andersherum in der Anwesenheit von starken Magnetfeldern:
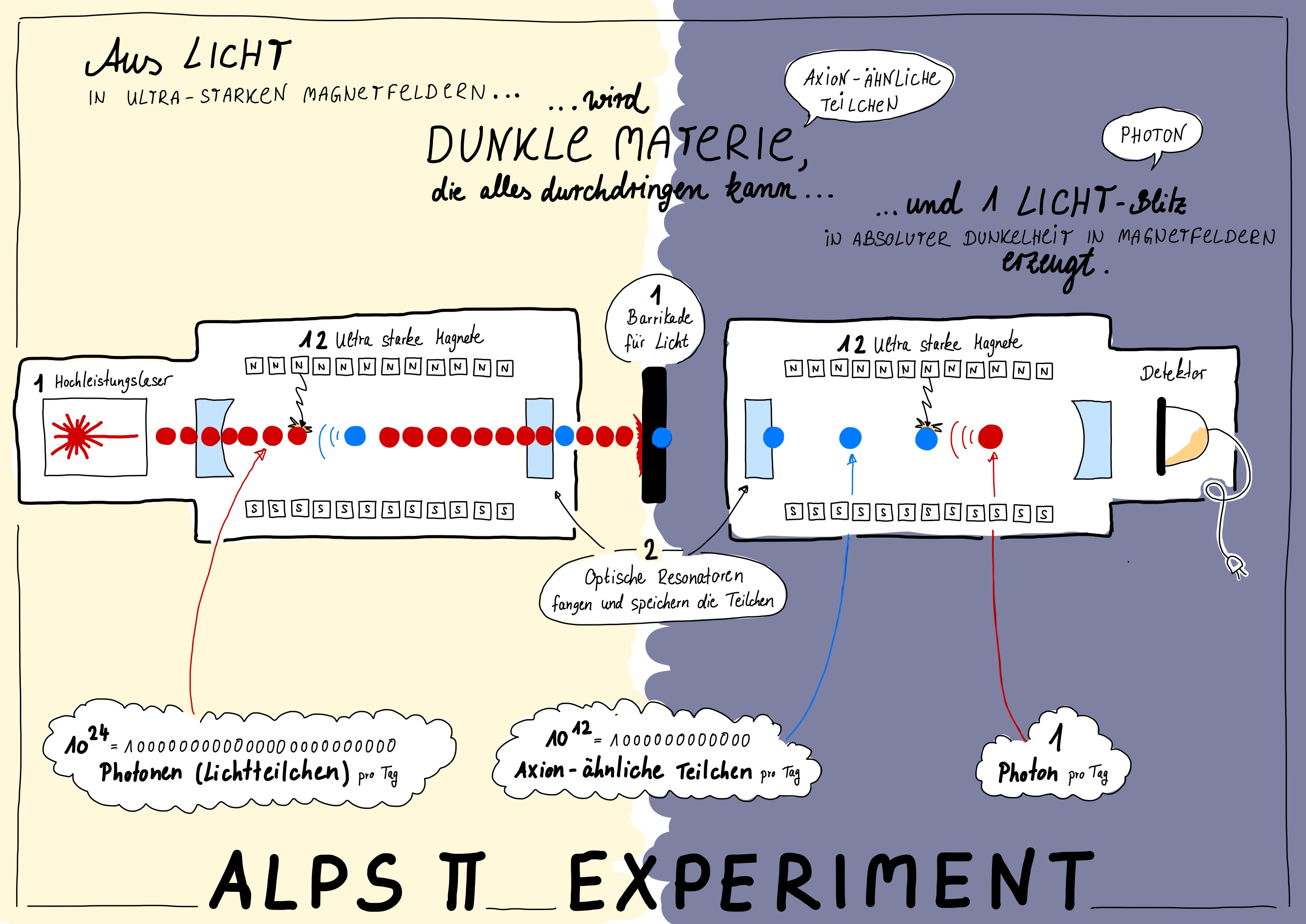
Abb. 133 Skizze des ALPS II Experiments am DESY.#
Ein Hochleistungslaser erzeugt eine große Menge an Lichtteilchen (Photonen). Er produziert \( P = 30\,\mathrm{W} \) bei einer Lichtwellenlänge von \( \lambda = 1064\,\mathrm{nm}\). Mit der Lichtgeschwindigkeit \(c \approx 3\cdot 10^8\,\mathrm{m/s}\) und \(h = 6{,}626\cdot 10^{-34}\,\mathrm{Js}\) dem Planck’sche Wirkungsquantum entspricht dies etwa \(10^{20}\) Photonen pro Sekunde:
Diese Photonen durchqueren ein möglichst langes (bei ALPS II \(L = 106\,\mathrm m\)) und starkes (\(B = 5\,\mathrm T\)) Magnetfeld um aus Licht Axion-ähnliche Teilchen zu generieren. Leider ist die Wahrscheinlichkeit für diesen Prozess ist sehr gering. Wir nennen dies auch den \(g_{a\gamma\gamma}\)-Faktor, der die Kopplung von Licht an Dunkle Materie beschreibt und eine sehr kleine Zahl sein muss (ansonsten hätten wir die Axion-ähnlichen Teilchen nämlich schon längst gefunden):
Angenommen es wurden Axion-ähnliche Teilchen generiert, so durchqueren diese eine Wand in der Mitte des Aufbaus, die Licht nicht durchdringen kann (nur Dunkle Materie kann da durch, da diese nicht wechselwirkt). Diese Art des experimentellen Aufbaus wird daher auch häufig als Light-Shining-Through-A-Wall-Experiment bezeichnet.
Auf der anderen Seite der Wand werden die Axion-ähnlichen Teilchen mithilfe eines weiteren Magnetfeldes (\(L = 106\,\mathrm m\), \(B = 5\,\mathrm T\)) in Licht umgewandelt, da wir sie sonst nicht detektieren können. Dies funktioniert nur, wenn Axion-ähnliche vorhanden sind, d.h. wenn sie produziert wurden und durch die Wand gekommen sind. Das Licht hat dann die gleiche Wellenlänge wie das Anfangslicht des Hochleistungslasers, aus welchem die Axion-ähnlichen Teilchen generiert wurden.
Falls keine Photonen detektiert werden, könnte dies bedeuten, dass keine Axionen erzeugt wurden oder die Umwandlungswahrscheinlichkeit geringer ist als vermutet.
Weitere Experimente
Andere Experimente wie BabyIAXO oder Madmax suchen nach Axionen aus dem Weltall. Das heißt sie benutzen nur den hinteren Teil des ALPS II Experimentes als Detektor, indem sie Axionen aus dem Weltall in Licht umwandeln. Vorteil ist, dass diese Experimente eine viel stärkere Axionen-Quelle haben, nämlich das Weltall. Nachteil ist, dass diese Axionen-Quellen nur existieren, wenn unsere kosmologischen Theorien wirklich stimmen. Mit ALPS II prüfen wir die Existenz von diesen Teilchen unabhängig von kosmologischen Theorien, direkt im Labor, was ziemlich cool ist. Wir produzieren immerhin Dunkle Materie in Hamburg in 30 Meter Tiefe.
Signalstärke#
Leider ist die Signalstärke am Ausgang des Experimentes sehr schwach, weil die Umwandlungswahrscheinlichkeit so gering ist. Zusammengenommen mit der Länge und Stärke des Magnetfeldes erhalten wir am Ende des Experimentes 1 Photon alle \(\tau = 700000\) Jahre:
Die Signalstärke kann erhöht werden, indem wir die Lichtteilchen des Hochleistungslasers dazu zwingen, möglichst lange im Magnetfeld zu bleiben. Hochreflektierende Spiegel fangen das Licht ein und sorgen dafür, dass es immer hin und her reflektiert. Dies nennt man auch einen optischen Resonator. Solche Resonatoren kommen auch in Gravitationswellendetektoren zum Einsatz, um die Empfindlichkeit von Laserinterferometern zu erhöhen. Mit Resonatoren auf beiden Seiten der Wand können durchschnittlich Verbesserungen von 5000-10000 pro Resonator (\(\beta_1, \beta_2\)) erreicht werden, wodurch sich das zu messende Signal auf 1 Photon pro Tag erhöht:
Show code cell source
import numpy as np
# Konstanten
λ = 1064e-9 # Wellenlänge des Lichts in m
c = 299792458 # Lichtgeschwindigkeit in m/s
h = 6.626e-34 # Planck-Konstante in Js
E = h * c / λ # Energie eines Photons
g_aγγ = 2e-11 # Kopplungskonstante in 1/GeV
B = 5 # Magnetfeldstärke in Tesla
L = 106 # Magnetfeldlänge in Metern
eta = 1 # Modenüberlapp
beta_1 = 10000 # Power build-up in der Production Cavity
P_PC = 30 # Optische Leistung in W
beta_2 = 10000 # Power build-up in der Regeneration Cavity
N_i = P_PC/E # Anzahl der Photonen in der Production Cavity pro Sekunde
tau = 3600*24 # Beobachtungszeit
# Berechnung der Photonenanzahl
N_γ = (1/16) * (g_aγγ * B * L)**4 * eta * beta_1 *beta_2 * N_i * tau
print(f"Anzahl der Photonen pro Tag im ALPS II Experiment: {N_γ}")
Anzahl der Photonen pro Tag im ALPS II Experiment: 1.0954888688232658
Einzelphotonen-Detektoren#
Selbst ein Photon pro Tag ist immer noch ein extrem schwaches Signal und erfordert hochspezialisierte Detektoren, sogenannten Quantendetektoren. Am DESY werden zwei Detektorsysteme untersucht, die beide in der Lage sind, einzelne Photonen zu detektieren.
Laserinterferometer#
Aktuell wird ein sogenanntes kohärentes Detektionsschema verwendet, was auf einem heterodynen Laserinterferometer basiert. Hier wird nach Lichtteilchen einer ganz bestimmten Wellenlänge (Frequenz) gesucht, die genau die richtige Schwebungsfrequenz im Laserinterferometer erzeugen. Diese Art von Laserinterferometer soll auch in Gravitationswellendetektoren im Weltraum verwendet werden.
Siehe auch
Wie funktioniert Laserinterferometerie?
Die genaue Kenntnis der Laserfrequenz ist hierfür notwendig und wird mittels aufwendigen und extrem phasenstabilen Regelschleifen kontrolliert. Die Regelschleifen sorgen dafür, dass ein Laser immer die exakte Frequenz an alle Sub-Systeme liefert, d.h. er ist die Referenz für alle Messungen. Sollte nun ein Lichtteilchen aus einem Axion-Teilchen entstehen, so kennen wir die Eingangsfrequenz enorm präzise und suchen nach genau dieser Frequenz auch am Ausgang des Experimentes. Alle anderen Frequenzen interessieren uns nicht, bzw. wir wissen, dass diese nicht das Signal beinhalten. Dadurch können wir beispielsweise weitere Laserfrequenzen benutzen um die optischen Resonatoren zu stabilisieren (der Abstand von zwei Spiegeln, die einen Resonator bilden, muss immer genau einem Vielfachen der Wellenlänge des Lichts entsprechen). Indem wir die Frequenz am Detektor identifizieren, können wir dieses Licht von dem Signallicht (Axion-Licht) sehr gut unterscheiden.
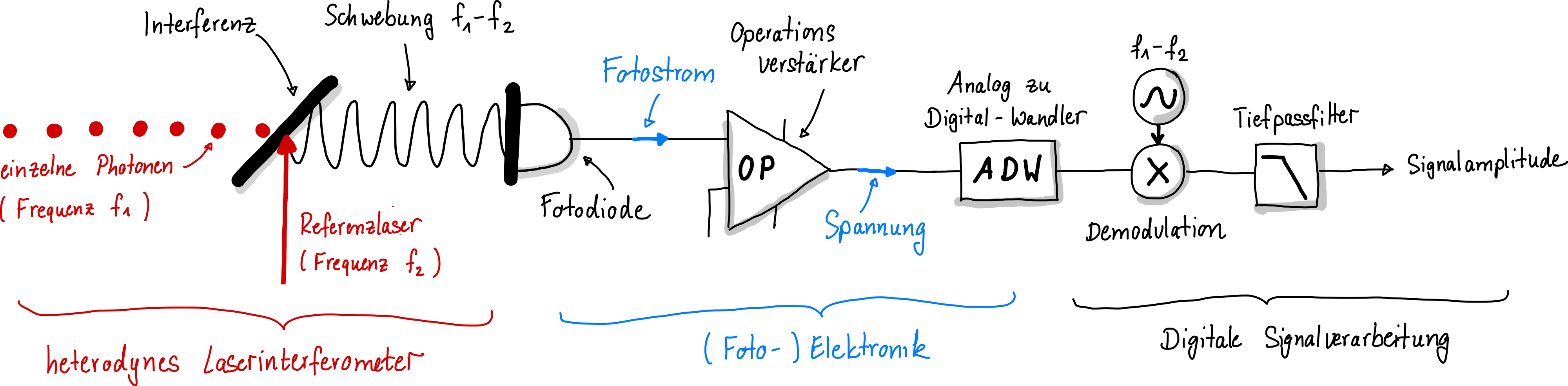
Abb. 134 Arbeitsprinzip eines heterodynen Laserinterferometers zur Messung schwacher Lichtsignale.#
Fehlt Axion-Licht am Detektor, wird keine Schwebungsfrequenz generiert und man misst lediglich die konstante Leistung des Referenzlasers. Diese fluktuiert leicht, was als Schrotrauschen bekannt ist. Schrotrauschen ist zufälliges Rauschen, was sich über lange Messzeiten wegmittelt, da es nicht kohärent ist. Das Rauschlevel geht also mit der Zeit runter! Tritt jedoch ein Axion-Lichtteilchen auf, erscheint plötzlich ein Signal bei einer bestimmten Frequenz. Dieses Signal ist kohärent und oszilliert bei der exakt richtigen Frequenz. Kohärente Signale mitteln sich über die Zeit nicht weg, sondern bleiben konstant. Während also ohne Signal das Rauschen abnimmt, zeigt sich bei einem Signal ein konstantes Plateau. Die Höhe dieses Plateaus verrät die Anzahl der erzeugten Photonen. Bei sehr wenigen Photonen ist eine lange Messdauer erforderlich, um das Plateau zu erkennen.
Phasenübergangsthermometer#
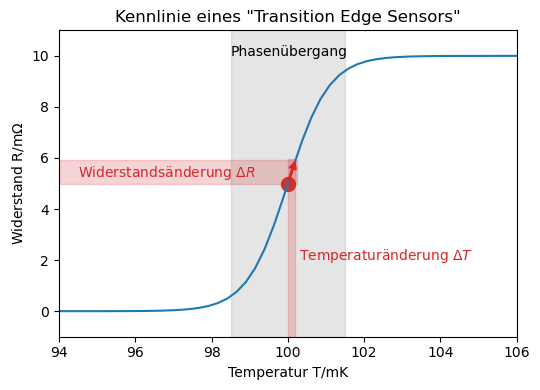
Als zweiten Detektor erforschen wir den Transition Edge Sensor (Phasenübergangsthermometer). Im Prinzip handelt es sich hierbei um ein extrem empfindliches Thermometer, was seinen Widerstand (\(R + \Delta R\)) bei Temperaturänderungen (\(\Delta T\)) ändert. Um hohe Empfindlichkeiten für kleinste Temperaturänderungen zu erreichen, nutzen wir den Effekt der Supraleitung. Im supraleitenden Zustand verschwindet der Widerstand eines Materials (wir benutzen Wolfram) fast vollständig (\(R = 0\,\Omega\)). Betrieben wird das Material an seiner kritischen Temperatur, dem Übergang zwischen normalleitendem und supraleitendem Zustand. Die Kennlinie eines solchen Thermometers zeigt, dass die kritische Temperatur sehr niedrig sein kann, hier \(100\,\mathrm{mK}\). Das Thermometer muss daher mittels Helium-Kryostaten nahezu auf den absoluten Nullpunkt (\(100\,\mathrm{mK}\)) gekühlt werden, um den supraleitenden Zustand zu erreichen.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
plt.rcParams['font.size'] = 10 # Schriftgröße
fig, ax = plt.subplots(figsize=(5.5, 4))
#--------- Transition Edge Sensor -------------
T = np.linspace(94, 106, num=50)
def R(T):
k = 1.86 # in 1/mK
a = 0.01 # in Ohm
Tk = 100 # in mK
return a / (1 + np.exp(-k * (T - Tk)))
# Plot
plt.plot(T, R(T) * 1000, color='tab:blue')
plt.xlabel('Temperatur T/mK')
plt.ylabel(r'Widerstand R/m$\Omega$')
plt.ylim([-1,11])
plt.xlim([94,106])
plt.title('Kennlinie eines "Transition Edge Sensors"')
# Scatter points
point1 = (100, R(100) * 1000)
point2 = (101, R(101) * 1000)
plt.scatter(*point1, color='tab:red', lw=5)
#plt.scatter(*point2, color='tab:red', lw=5, alpha=0.5)
# Draw arrow along the curve
t_values = np.linspace(100, 101, num=10)
r_values = R(t_values) * 1000
mid_point = len(t_values) // 4
plt.annotate('', xy=(t_values[mid_point], r_values[mid_point]), xytext=point1,
arrowprops=dict(arrowstyle='->', color='tab:red', lw=2))
# Highlight supraleitender Bereich
#plt.fill_between(T, 0, -1, color='gray', alpha=0.2)
plt.axvspan(98.5, 101.5, color='gray', alpha=0.2)
plt.axvspan(100, 100.2, ymin = 0.0, ymax = 0.58, color='tab:red', alpha=0.2)
plt.axhspan(R(100) * 1000, R(100.2) * 1000, xmin=0.0, xmax=0.52, color='tab:red', alpha=0.2)
plt.annotate('Phasenübergang', xy=(98.5,10))
plt.annotate(r'Temperaturänderung $\Delta T$', xy=(100.3,2), color = 'tab:red')
plt.annotate(r'Widerstandsänderung $\Delta R$', xy=(94.5,5.25), color = 'tab:red')
plt.tight_layout()
plt.show()
Wenn nun kleinste Energiemengen \(E\), beispielsweise in Form eines einzelnen Photons, absorbiert werden und dadurch eine geringfügige Temperaturerhöhung (\(\Delta T\)) verursacht wird, ändert sich der Widerstandswert (\(\Delta R\)) abrupt. Dies ermöglicht die Messung von Temperaturen im Mikrokelvin-Bereich. Die Widerstandsänderung verursacht einen Strompuls im System, der mittels supraleitender Elektronik (SQUID: superconducting interference device) in einen Spannungspuls umgewandelt wird. Hierbei wird eine Spule benutzt, die aufgrund der Stromstärkeänderung ein Magnetfeld generiert. Dieses Magnetfeld wird an eine weitere Spule gekoppelt, in der eine Spannung induziert wird. Dies ist im Prinzip ein superempfindliches Magnetometer.
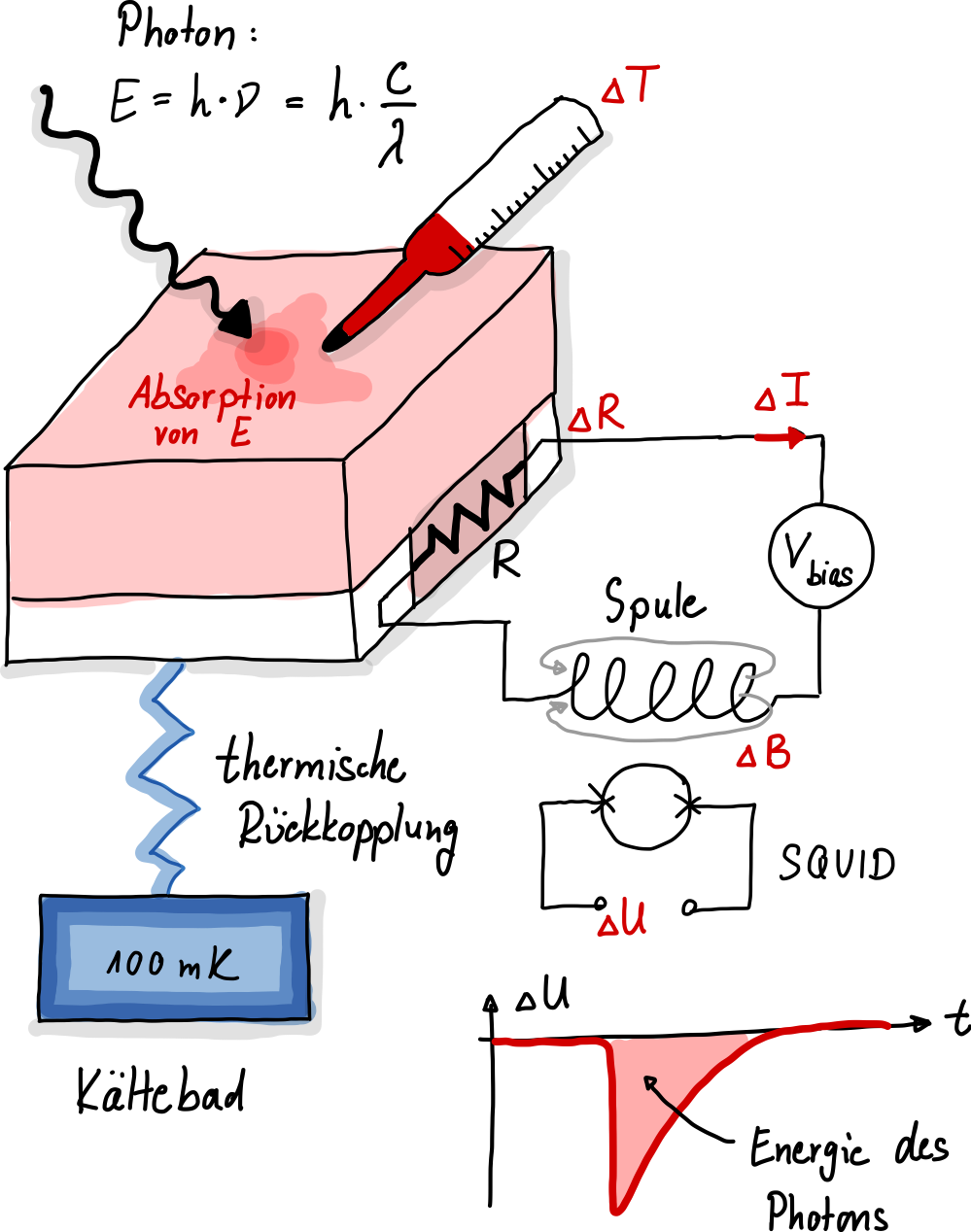
Abb. 135 Arbeitsprinzip eines supraleitenden Thermometers zur Detektion einzelner Photonen.#
Im ALPS II Experiment müssen wir Photonen mit einer Wellenlänge von \( \lambda = 1064\,\mathrm{nm} \) messen, was einer Energie von lediglich
entspricht.
Diese Energie ist ausreichend, um in einem Wolfram-Absorber eine Temperaturdifferenz von einigen \(100\,\mu\mathrm{K}\) zu erzeugen. Ein Photon mit kürzerer Wellenlänge, etwa \(\lambda = 532\,\mathrm{nm} \) (grünes Licht), hätte eine deutlich höhere Energie, was zu einem stärkeren Anstieg von Temperatur und Widerstand führen würde. Somit ermöglicht dieser Detektor die Unterscheidung von Photonen unterschiedlicher Energie, Frequenz oder Wellenlänge. Im nachfolgenden Diagramm kann die Pulshöhe verändert werden. Dadurch ändert sich auch die Fläche unter dem Puls, was ein Maß für die Energie des Photons ist.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML
plt.rcParams['font.size'] = 12; # Schriftgröße
fig, ax = plt.subplots(figsize=(5, 3), tight_layout=True)
t = np.linspace(0, 1e-4, num=10000)
k = 1e-5
def animate(a_in):
ax.clear()
a = a_in * 1e-3
t_0 = 0.2e-4
tau_minus = 4.92e-6
tau_plus = 0.34e-6
pulse = k - ((2*a) / (np.exp((t-t_0)/tau_minus) + np.exp(-(t-t_0)/tau_plus)))
#t_0 = 0.4e-4
#pulse2 = k - ((4*a) / (np.exp((t-t_0)/tau_minus) + np.exp(-(t-t_0)/tau_plus)))
ax.plot(t*1000,pulse*1000, color = 'tab:red')
#plt.plot(t*1000,pulse2*1000, label ='Photon, 532nm', color = 'tab:green')
# Füllen der Fläche unter den Kurven
ax.fill_between(t*1000, pulse*1000, color='tab:red', alpha=0.3)
#plt.fill_between(t*1000, pulse2*1000, color='tab:green', alpha=0.3)
ax.set_xlabel('Zeit (ms)')
ax.set_ylabel('Spannung (mV)')
# plt.legend()
ax.set_xlim([0,0.1])
ax.set_ylim([-15,0.1])
# Create an animation by varying fs from 1 to 10 with a step of 1
ani = FuncAnimation(fig, animate, frames=range(10, 1), repeat=False)
# Display the animation
#fig.tight_layout()
plt.close()
HTML(ani.to_jshtml())
/Users/KSIsleif/opt/anaconda3/lib/python3.9/site-packages/matplotlib/animation.py:1719: UserWarning: Can not start iterating the frames for the initial draw. This can be caused by passing in a 0 length sequence for *frames*.
If you passed *frames* as a generator it may be exhausted due to a previous display or save.
warnings.warn(
Man erkennt, dass das System sehr schnell die Energie absorbiert (sehr steile Flanke am Anfang). Um bereit für den nächsten Puls zu sein, wird das System über eine thermische Verbindung an ein Kältebad gekoppelt. Man sieht, dass diese Rückkopplung einige Zeit benötigt, da der Puls nur langsam abfällt. In diesen simulierten Pulsen habe wir eine Anstiegszeit von \(0{,}34\,\mathrm{\mu s}\) und eine Abfallszeit von \(5\,\mathrm{\mu s}\) angenommen.
Vergleich#
Das Phasenübergangsthermometer bietet eine geringere Energie-Auflösung als das heterodyne Detektionssystem. D.h. mit dem Phasenübergangsthermometer können wir Photonen unterscheiden, die eine Energiedifferenz von 5-10% aufweisen. Das heterodyne System hingegen erreicht eine deutlich höhere Energieauflösung durch seine schmalbandige Eigenschaft. Schon geringfügige Abweichungen von der Ziel-Schwebungsfrequenz führen dazu, dass der Detektor das Photon nicht erkennt. Beispielsweise würde ein Signal bei 2,4 Hz erkannt, aber bereits bei 2,4003 Hz nicht mehr, was einer Auflösung von besser als 0,01% entspricht. Dies macht den Detektor auch weniger anfällig für Rauschen, da es im Labor oder Experiment auch so schon einzelne Lichtteilchen gibt, die zufällig mal den Detektor treffen können. Durch Wärmestrahlung von Objekten wird die ganze Zeit Infrarotstrahlung ausgesendet, die einen ähnlichen Wellenlängenbereich aufweist wie die zu detektierenden einzelnenden Axion-Photonen. Nachteil des heterodynen Systems ist, dass es nur Photonen-Raten (also Photonen pro Zeit) messen kann und nicht einzelne Photonenpulse.


