Satellitennavigationssysteme#
Positionsbestimmung#
Positionsbestimmung mittels Satellitennavigationssystemen basiert auf dem Messprinzip der Triangulation. Mehrere Satelliten befinden sich einem Orbit der Erde und umkreisen diese. Mit einer bestimmten Rate sendet jeder Satellit seine Uhrzeit und Position regelmäßig aus. Die genaue Uhrzeit erhält jeder Satellit durch eine Atomuhr (tatsächlich sogar zwei, eine Cäsium und eine Rubidium), die an Bord mitfliegt.
Ein Empfänger auf der Erde benötigt die Signale von insgesamt vier Satelliten und seine Position möglichst präzise zu bestimmen. Der Empfänger hat seine eigene Zeitbasis und ermittelt für jedes der vier Satellitensignale die Sendezeit. Mittels dieser Laufzeitmessung weiß der Empfänger, in welchem Abstand er sich zu den vier Satelliten befindet, solange die Geschwindigkeit der ausgesandte Satellitensignale als konstant angenommen werden kann:
Rein geometrisch kann man sich das so vorstellen, dass jeder der vier Satelliten ein GPS-Signal in Form einer Kugelwelle aussendet. Der Schnittpunkt der vier Kugelwellen ist die Position des Empfängers. Theoretisch würden hierfür auch nur 3 Satelliten ausreichen. Der 4. Satellit dient dazu die mitunter ungenaue Zeitmessung seitens des Empfängers zu verbessern.
Es gilt wieder: Je mehr desto besser. Wird die Anzahl der Satelliten erhöht, so können Ungenauigkeiten in der Positionsermittlung reduziert werden.
Der Einfluss der Relativitätstheorie#
Während des Flugs eines Satelliten kommen auch relativistische Effekte mit ins Spiel. Bewegt sich eine Uhr so erfährt sie eine Zeitdilaation nach Einsteins spezieller Relativitätstheorie. Bewegte Uhren gehen langsamer gegenüber einee stationären Uhr. Je geringer die Erdumlaufbahn eines Satelliten, desto schneller ist der Satellit und desto größer wird dieser Effekt. Andererseits besagt die Allgemeine Relativitätstheorie, dass Uhren in schwächeren Gravitationsfeldern schneller gehen, was diesem Effekt entgegenwirkt. Diese beiden Effekte sind jedoch nicht immer gleich und hängen von der Absoluthöhe und anderen Parametern ab. Die GPS-Satelliten bewegen sich etwa mit \(3,87\,\mathrm{km/s}\) relativ zu Erde, wodurch die Uhren langsamer gehen. Dadurch dass das Erdschwerefeld jedoch mit der Höhe abnimmt, wird dieser Effekt kompensiert, und die Uhren laufen sogar am Ende schneller, um etwa \(4,5 \cdot 10^{-10}\,\mathrm s\) pro Sekunde. Dies entspricht \(38\,\mathrm{ms}\) pro Tag.
Geschwindigkeitsbestimmung#
Mittels der Satellitendaten und der Signallaufzeiten lässt sich nicht nur die Position bestimmen, sondern auch die Geschwindigkeit des Empfängers. Hierfür kann entweder die Dopplereffekt im Satellitensignal gemessen werden, oder man differenziert den Ort nach der Zeit. Beides ist nur möglich, nachdem sich der Empfänger bewegt hat!
Satelliten und Umlaufbahnen#
Aktuell gibt es verschiedene Satellitensysteme in Erdumlaufbahnen, die im Einsatz sind:
GPS (Global Positioning System), bzw. der ausführliche Name NAVSTAR GPS (Navigational Satellite Timing and Ranging), USA
GLONASS (Global Navitation Satellite System), Russland
Galileo, Europa
BeiDou, China
Die 25-30 GPS-Satelliten befinden sich auf einer Erdumlaufbahn in etwa 20.200km Höhe, wobei sich deren Position ständig ändert. Es gibt insgesamt 6 Bahnebenen, die um 55° gegen den Äquator geneigt sind. Die Satellitenkonstellation in diesen Bahnebenen wurde so gewählt, dass immer mindestens 4 Satelliten weltweit für die Positionsbestimmung zur Vefügung stehen. Dies gilt jedoch nicht für die Polregionen, hier müssen andere Satellitensysteme anstelle von GPS eingesetzt werden, den Satelliten in anderen Bahnen fliegen.
Jeder Satellit umkreist die Erde zweimal in etwa 24h (um genau zu sein innerhalb eines Sterntags).
Sollte ein Satellit einmal ausfallen, gibt es verschiedene Prozedere:
ein neuer Satellit wird gestartet
ein schalfender Satellit in der Umlaufbahn wird aktivitiert
ein aktiver Satellit wird an eine andere Position manövriert
Jede dieser Prozeduren ist sehr zeitintensiv und es kann Monate dauern, bis der ausgefallene Satellit ersetzt wird. Satelliten haben sehr schwache Triebwerke und kann sich nicht selber in höhere Umlaufbahnen befördern. Der Treibstoff dient eigentlich nur dafür, dass exakte Position in der Umlaufbahn zu behalten und kann nur begrenzt dafür eingesetzt werden, mittels einer Folge von Brems- und Beschleunigungsmanövern eine neue Position anzusteuern.
Daten#
Die Daten für Empfänger auf der Erde werden alle 30s ausgesendet. Die aktuelle Genaugikeit der Positionsbestimmung liegt bei etwa 2m. Mittels Differential-GPS (DPGS) kann die Genauigkeit auf Milimeter verbessert werden! Das DGPS benötigt hierfür eine Referenzstation auf der Erde die sich in der Nähe des Empfängers befindet. An diese Referenzstation sendet der Satellit zusätzliche Daten mit entsprechenden Messabweichungen, die beispielsweise durch die Atmosphärenzusammensetzung und Temperatur verursacht werden. Mittels Sensorik an Bord kann der Satellit diese Messabweichungen abschätzen und zur Verfügung stellen. Der Empfänger kann Kontakt zu der Referenzstation aufnehmen und seine Positionsmessung mittels der Referenzdaten korrigeren. In Deutschland übernimmt diese Aufgabe SAPOS, den Satellitenpositionierungsdienst der deutschen Landesvermessung. Die Korrekturdaten können in einem Internetprotokoll in Echtzeit abgerufen werden (https://sapos.de).
Die Position eines Satelliten beinhaltet folgende Informationen (6 Kepler Elemente):
Größe und Proportionen der Kepler-Ellipse
Halb-Hauptachse von etwa 26.560km für GPS Satelliten
Ekzentrität von etwa 0,02 oder kleiner für GPS Satelliten
Orbitebene:
Inklination/Kippung (z.B. 55° gegenüber des Äquators)
Longitude
Position der Ellipse und des Satelliten:
Perigee Argument
Anomalien
In Realität reichen diese 6 Parameter jedoch nur bedingt aus, um die genaue Position eines Satelliten zu ermitteln. Externe Störungen, wie z.B. Gravitationseinflüsse von Mond, Sonne und Strahlung beeinflussen die reale Satellitenbahn. Daher beinhaltet die GPS Nachricht zudem die Rate, mit welcher sich die Parameter ändern. Dadurch kann der Empfänger Korrekturen der Bahntrajektorie durchführen.
Dadurch, dass man jetzt die Position des Satelliten im Orbit kenntn, können die x,y,z Koordinaten auf der Erde aus den Kepler-Bahnen bestimmt werden. Die Berechnung wollen wir uns nicht genauer ansehen, doch sie ist mitunter nicht gant trivial, da hierbei auch die Erdrotation miteinbeziehen muss, die vergangen ist, während Sender und Empfänger miteinander kommunizieren.
Woher kennt der Satellit diese Daten?#
Alle GPS Satellinte werden von Stationen auf der Erde nachverfolgt. Diese Stationen sind Teil des Kontrollsegmentes des GPS Systems, welches die Satelliten und deren Nachrichten überwacht. Alle zwei Stunden werden Orbitparameter und Uhrenjustierungen auf den Satelliten neu hoch geladen.
Signale#
Der Satellit misst seine eigene Umlaufbahn mit Sensoren an Bord und sendet Funksignale mit einer Frequenz von früher 100-500MHz, und heutzutage bis zu 20GHz aus. Diese Radiosignale wird entsprechend codiert, d.h. deren Positionsdaten und andere Informationen werde auf die Radiowelle aufmoduliert.
Der Satellit sendet alle 30 s ein Signal aus
Die Nachricht wird mit einer Datenrate von 50 bit / s aufgeprägt
Die Nachteinlänge beträgt 1500 Bits
Diese Daten werden auf zwei Frequenzen ausgesendet:
1575,42MHz: Dies ist die erste L1-Frequenz und überträgt zwei Codes:
für zivile Nutzung (C/A-Code = Coarse/Application)
trennbar-überlagert nicht-öffentliche Codes für die militärische Nutzung (P/Y-Code = Precision/Encrypted)
1227,60MHz: Dies ist die zweite L2-Frequenz und überträgt nur den P/Y-Code für militärische Zwecke. Wahlweise kann auf der zweiten Frequenz auch der C/A-Code übertragen werden.
Die Übertragung einer zweiten Frequenz erlaubt es Störeffekte aus der Ionosphäre zu eliminieren, die die Übertragungsgeschwindigkeit beeinflussen.
1176,45MHz: Die ist die dritte L5-Frequenz, welche sich im Aufbau befindet.
Navigations-Nachricht#
In Abb. 121 ist im Zeitverlauf die Codierung eines GPS-Signals dargestellt.
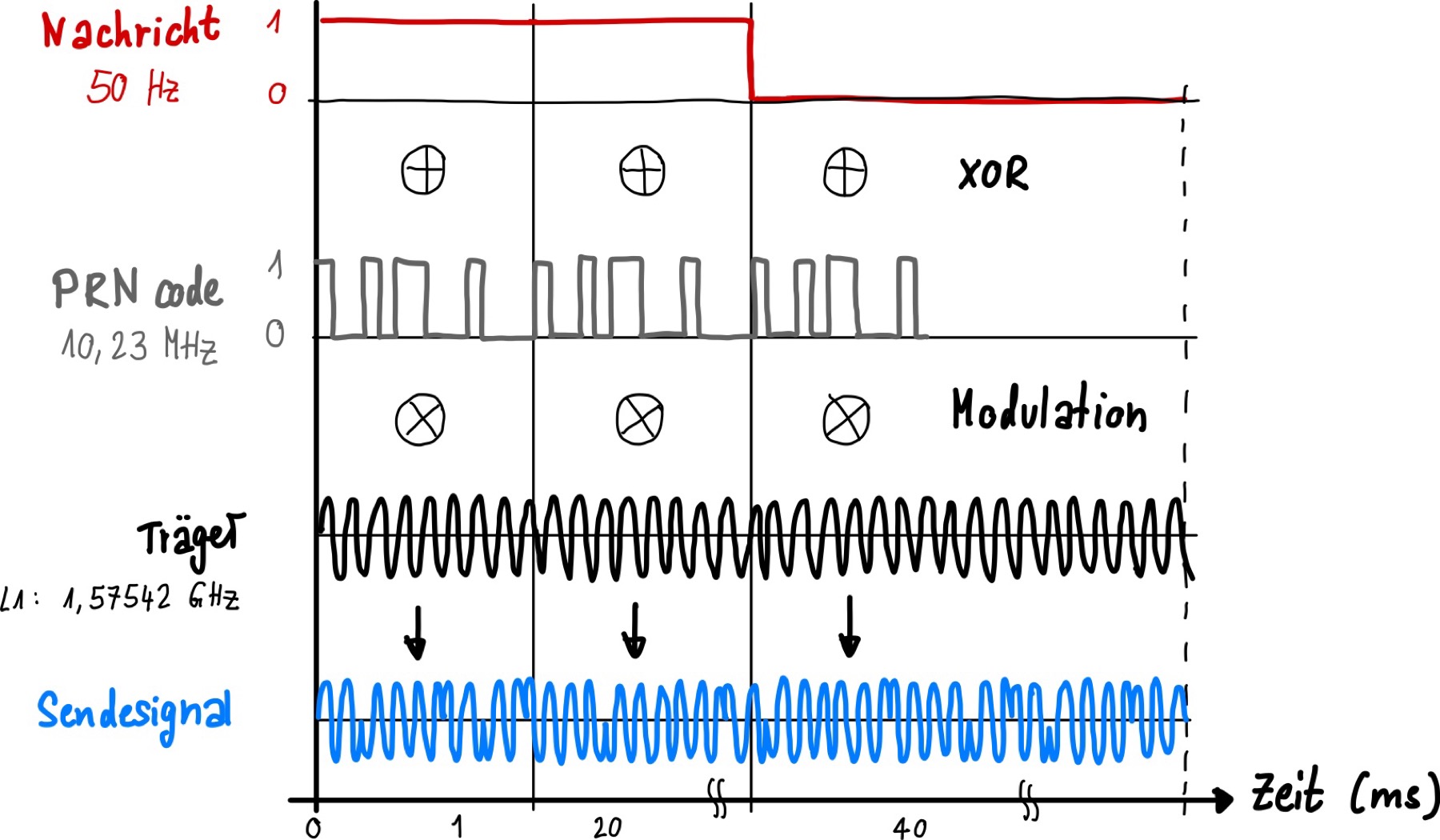
Abb. 121 Codierung der GPS-Signal. (PRN: Pseudo Random Noise)#
Die Navigations-Nachricht enthält die Informationen über Position und Zeit, was in eine binäre Zahlenfolge, bestehend aus 0 und 1, umgewandelt wird.
Die Frequenz des Signals beträgt 50 Hz (50 bit / s)
Die einzelne Bit-Länge beträgt 20 ms
Die Nachricht besteht aus 1500 Bits (= 5 x 30 Bits), dies nennt man auch den Frame (Rahmen). Ingesamt gibt es 25 Frames, jeder dieser Frames besteht aus 5 Subframes mit jeweils 10 Worten mit je 30 bit.
Die ersten zwei Worte jedes Subframes haben immer die gleiche Struktur:
Wort im Subframe: TLM, dies enthält eine feste Präambel, die leicht zu erkennen ist, und einige Bits zur Überprüfung.
Wort im Subframe: Das HOW Wort (Handover-Word) ist für die GPS-Funktionalität von entscheidender Bedeutung, da es den Subframe mit einem Zeitstempel versieht, der es dem Empfänger ermöglicht herauszufinden, wann er gesendet wurde.
Die restlichen 8 Wörter im Subframe enthalten je nach Subframe unterschiedliche Daten.
Subframe enthält die Korrekturen der Satellitenuhr und die Wochennummer der GPS-Zeit, die es dem Empfänger zusammen mit dem feineren Zeitstempel aus dem Übergabewort ermöglichen, die genaue Zeit zu berechnen, zu der die Nachricht gesendet wurde. Dieser Subframe enthält auch ein “Health”-Bit, das angibt, ob sich die Navigationsdaten in einem guten Zustand befinden. Wenn die Umlaufbahn eines GPS-Satelliten angepasst werden muss, schaltet das Kontrollsegment dieses Bit vorübergehend um, um den Empfängern mitzuteilen, dass sie sich nicht auf die Informationen dieses Satelliten verlassen sollten, wenn er seine Position ändert.
und 3. Subframe enthalten die bereits erwähnten Bahnparameter, erweitert um Geschwindigkeitsinformationen, die zusammen als Ephemeridenparameter bezeichnet werden - sie ermöglichen es dem Empfänger, die Position des Satelliten zu berechnen.
Die letzten beiden Subframes 4. und 5. enthalten die groben Ephemeridendaten für alle Satelliten - diese Sammlung ist als Almanach bekannt. Damit kann der Empfänger ungefähr abschätzen, wann ein neuer Satellit über dem Horizont auftauchen wird. Zu den weiteren Informationen, die in diesen Unterrahmen übertragen werden, gehören der Zustand anderer Satelliten und einige Parameter, mit denen der Empfänger versucht, die ionosphärische Verzögerung zu berücksichtigen. Die komplette Übertragung der Daten dauert 12,5 Minuten. Der komplette Almanach muss mindestens einmal bei der primären Initialisierung eines Empfängers durchgeführt werden.
Die Gesamtzeit der Übertragung beträgt somit mindestens 30 s (= 1500 x 20 ms) für die aktuelle GPS-Position. Die komplette Übertragung des kompletten Artikels würde 2,5 Stunden benötigen. Eine Übertragung des kompletten P/Y-Codes würde aufgrund der detaillierten Informationen theoretisch 276 Tage benötigen für eine vollständige Übermittlung der Daten. In der Praxis sendet jeder Satellit ein 7-tägiges Fragment aus.
Modulation der Nachricht auf den Träger#
Die Navigations-Nachricht wird in eine binäre Zahlenfolge konvertiert, welche auf die Funkwelle aufgeprägt wird. Diese Modulation kann über verschiedene Varianten geschehen, beispielsweise durch Multiplzieren der Trägerwelle (Funkwelle bei GHz-Frequenz) mit der binären Nachrichten-Folge, bestehend aus 0 und 1.
Show code cell source Hide code cell source
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
from scipy import signal
from random import randint, choice
import random
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
plt.rcParams['font.size'] = 10; # Schriftgröße
num = 200
fig, ax = plt.subplots(3,1,figsize=(6,3))
line0, = ax[0].plot([], [], lw=2, color = 'tab:blue')
line1, = ax[1].plot([], [], lw=2, color = 'tab:red')
line2, = ax[2].plot([], [], lw=2, color = 'tab:gray')
def init():
line0.set_data([], [])
line1.set_data([], [])
line2.set_data([], [])
return line0, line1, line2
ax[0].set_xlim(0,2)
ax[1].set_xlim(0,2)
ax[2].set_xlim(0,2)
ax[0].set_ylim(-0.1,1.1)
ax[1].set_ylim(-1.1,1.1)
ax[2].set_ylim(-1.1,1.1)
ax[0].axis('off')
ax[1].axis('off')
ax[2].axis('off')
ax[0].set_title('GPS-Nachricht:')
ax[1].set_title('Träger:')
ax[2].set_title('GPS-Nachricht x Träger:')
ax[0].axhline(y=0, lw = 1, color = 'tab:gray', ls = ':')
ax[1].axhline(y=0, lw = 1, color = 'tab:gray', ls = ':')
ax[2].axhline(y=0, lw = 1, color = 'tab:gray', ls = ':')
def animate(i):
x = np.linspace(0, 2, num)
y0 = 0.5*signal.square(2 * np.pi * 1 * (x - 0.01 * i))+0.5
y1 = np.sin(2 * np.pi * 10* (x - 0.01 * i))
y2 = (0.5*signal.square(2 * np.pi * 1 * (x - 0.01 * i))+0.5)*np.sin(2 * np.pi * 10* (x - 0.01 * i))
line0.set_data(x,y0)
line1.set_data(x,y1)
line2.set_data(x,y2)
return line0, line1, line2
anim = animation.FuncAnimation(fig, animate, init_func=init, frames=200, interval=20, blit=True)
plt.tight_layout()
plt.close()
HTML(anim.to_jshtml())


