Grundlagen der Elektrotechnik

Elektrotechnik Grundlagen, Ohm’sches Gesetzt, Knotensatz, Maschensatz, Zweipole | Prof. Griesbauer

In der Elektrotechnik bilden die elektrischen Grundgleichungen die Grundlage für das Verständnis elektrischer Schaltungen. Eine der fundamentalen Gleichungen ist das ohmsche Gesetz, welches den Zusammenhang zwischen Spannung, Strom und Widerstand beschreibt:

\[ R = \frac{U}{I} \]

Dabei repräsentiert \(R\) den elektrischen Widerstand, \(U\) die Spannung und \(I\) den Strom. Dieses Gesetz bildet die Basis für das Verständnis von elektrischen Schaltungen. In komplexeren Schaltungen werden oft mehrere Widerstände miteinander kombiniert. Es gibt zwei grundlegende Regeln für die Berechnung des Gesamtwiderstands solcher Kombinationen.

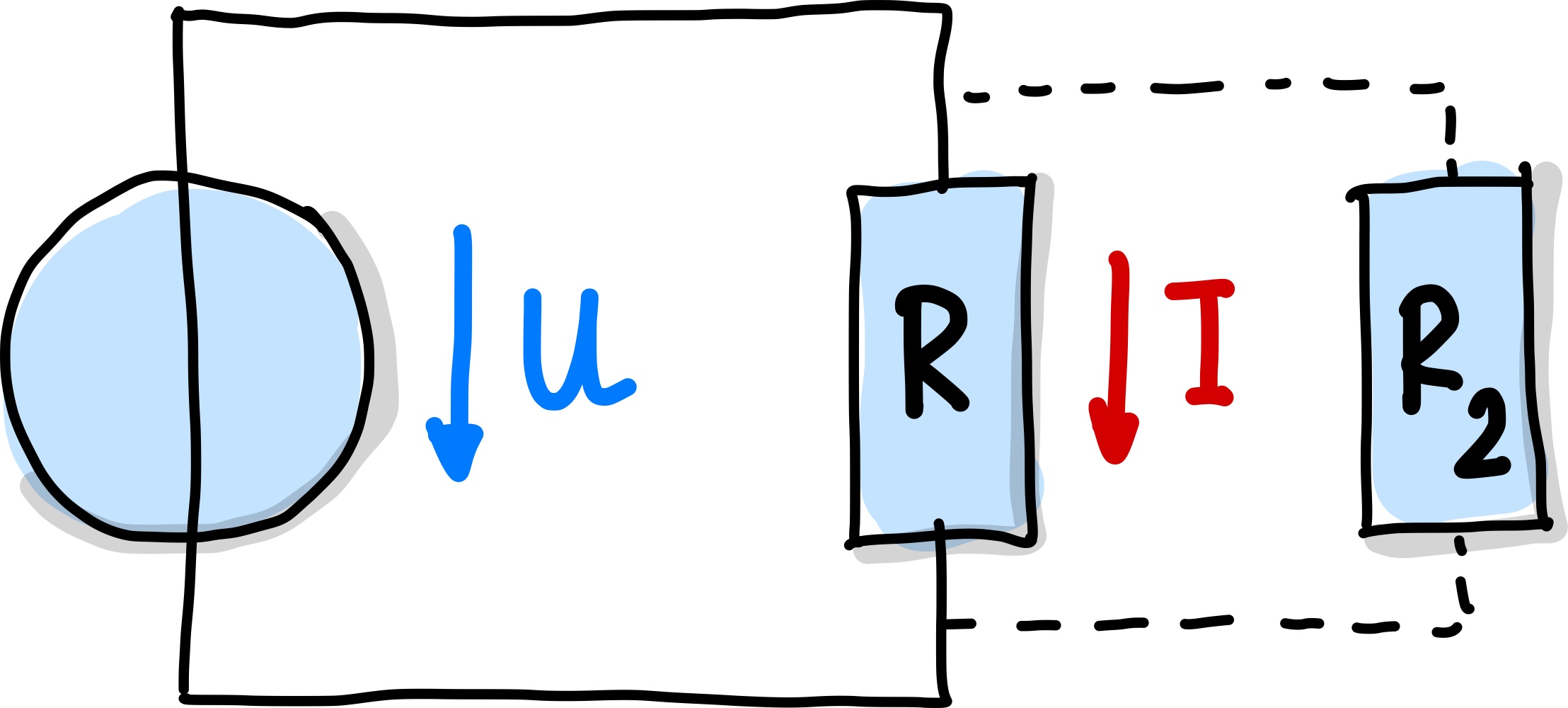
Abb. 65 Schaltbild zur Daratellung des Ohm’schen Gesetzes und Parallelschaltung von zwei Widerständen.

Parallelschaltung

Bei der Parallelschaltung von Widerständen ergibt sich der Gesamtwiderstand \(R_{\text{ges}}\) gemäß der Formel:

\[ \frac{1}{R_{\text{ges}}} = \frac{1}{R_1} + \frac{1}{R_2} \]

Reihenschaltung

In einer Reihenschaltung addieren sich die Widerstände einfach:

\[ R_{\text{ges}} = R_1 + R_2 \]

Diese Regeln sind einfach herleitbar und spielen eine entscheidende Rolle in der Elektrotechnik.

Kirchhoffsche Gesetze

Die Kirchhoffschen Gesetze sind fundamentale Prinzipien in der Elektrotechnik und ermöglichen die Analyse komplexer Schaltungen.

Knotenregel (Knotensatz)

Die Knotenregel besagt, dass die Summe der Ströme, die in einen Knoten hineinfließen, gleich der Summe der Ströme ist, die aus dem Knoten herausfließen. Mathematisch ausgedrückt:

\[ \sum_k I_k = 0 \]

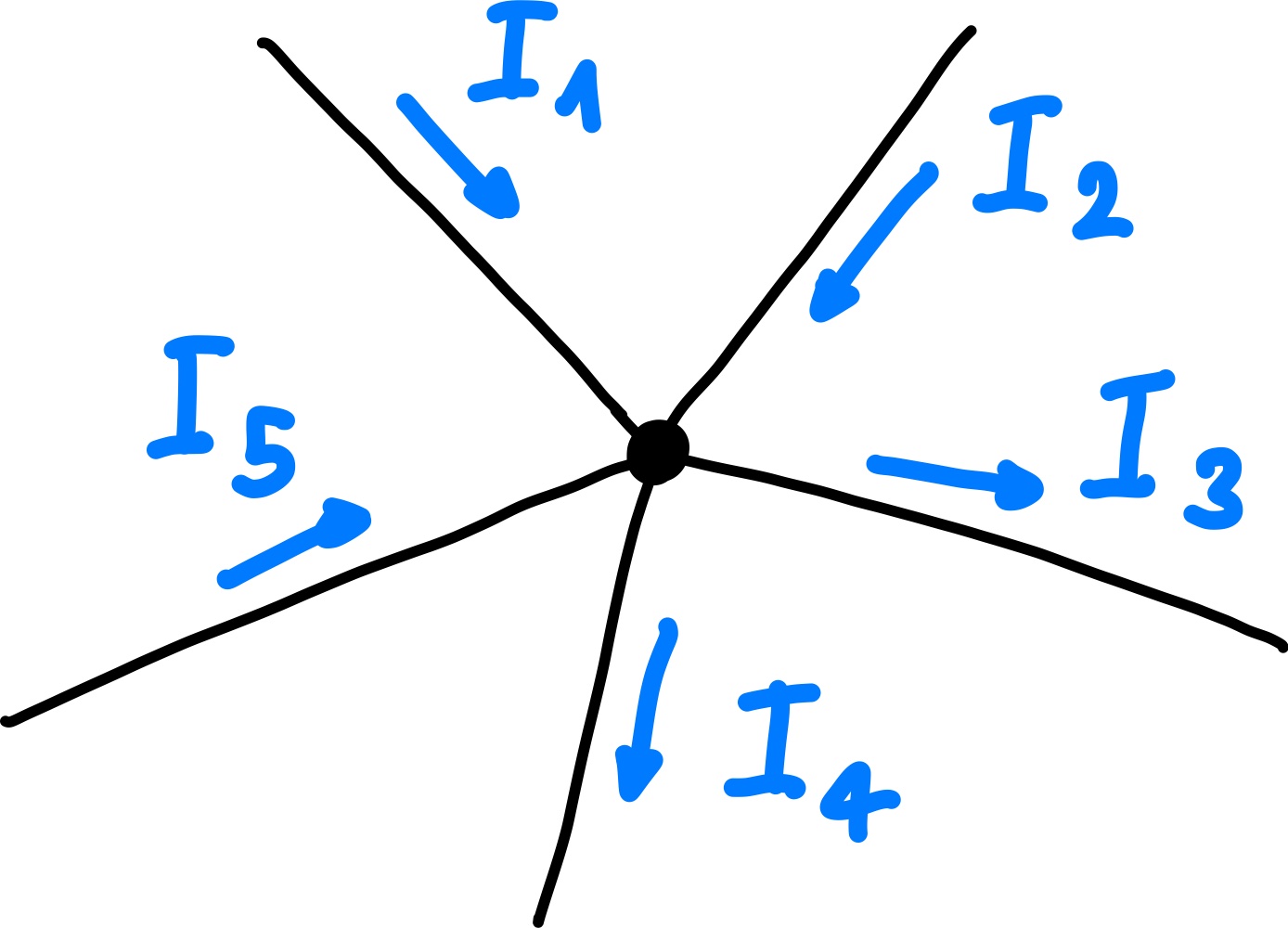
Abb. 66 Knotenregel.

Maschenregel

Die Maschenregel besagt, dass die Summe der Spannungen in einer geschlossenen Schleife (Masche) einer Schaltung immer null ist:

\[ \sum_k U_k = 0 \]

Unabhängig von der gewählten Masche oder dem gewählten Knoten gelten diese Regeln immer. Sie sind entscheidend für die Analyse und das Verständnis von elektrischen Schaltungen.

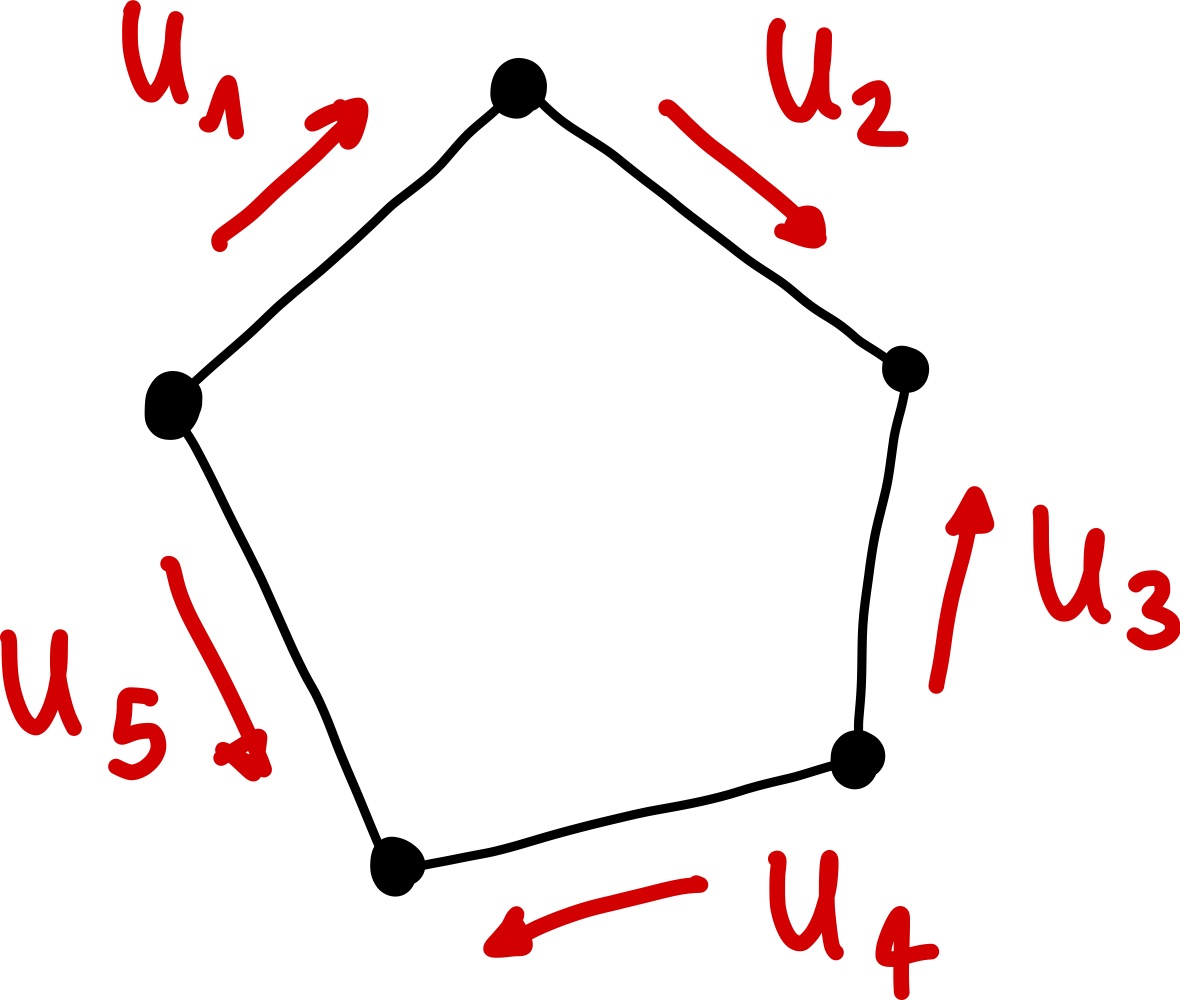
Abb. 67 Maschenregel.

Aktive Zweipol-Theorie

Die Zweipol-Theorie ermöglicht die Vereinfachung komplexer Schaltungen durch den Ersatz eines Teils der Schaltung durch einen einfachen Zweipol. Dieser Zweipol besteht aus einer Spannungsquelle und einem Innenwiderstand, was einer realen Spannungsquelle entspricht. Es gibt zwei Varianten: aktive und passive Zweipole.

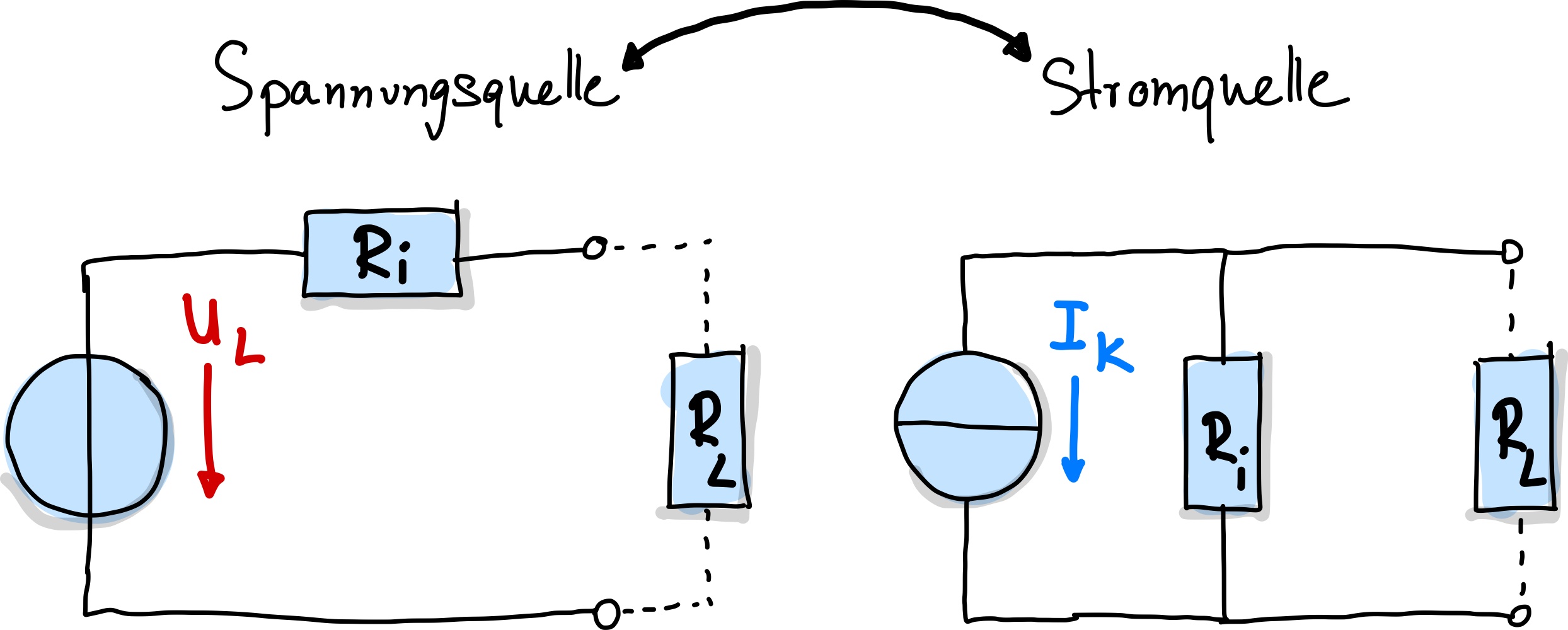
Abb. 68 Aktiver Zweipol.

Ein aktiver Zweipol enthält eine Spannungsquelle und wird durch die Leerlaufspannung \(U_L\) und den Innenwiderstand \(R_i\) definiert. Mathematisch ausgedrückt:

\[\begin{split} \begin{align*} U_L &= U_{\text{K}} \\ R_i &= \frac{U_L}{I_K} \end{align*} \end{split}\]

Die Bestimmung von \(U_L\), \(I_K\), \(R_i\) und \(G_i\) erfolgt durch geeignete Messungen unter bestimmten Bedingungen.

1. Zur Bestimmung der Spannung \(U_L\) und \(R_i\) nimmt man an, dass der Lastwiderstand \(R_L\) unendlich groß wird. Jetzt bestimmt man die Spannung, die an \(R_i\) bzw. \(R_L\) abfällt.

2. Zur Bestimmung des Kurzschlusstroms nimmt man \(R_L = 0\), also einen Kurzschluss, an.

3. Für die Innenwiderstabndsberechnung werden alle Spannungsquellen zu einem Kurzschluss und alle Stromquellen werden durchtrennt (unendlich hoher Widerstand)

Um die Anwendung dieser Regeln besser zu verstehen, betrachten wir einige Beispiele. Nehmen wir an, wir haben eine Spannungsquelle \(U_0\), an die zwei Widerstände \(R_1\) und \(R_2\) angeschlossen sind.

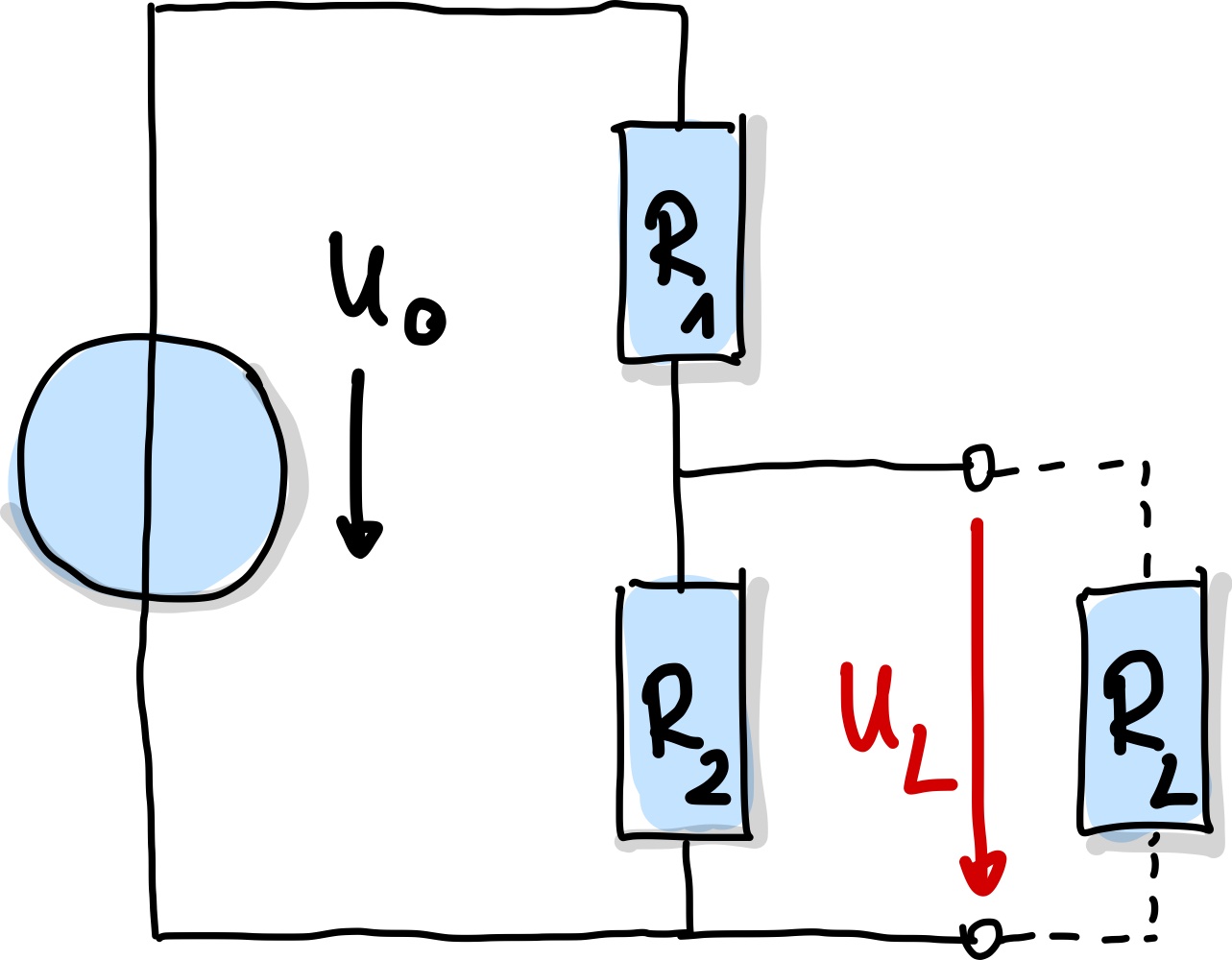
Abb. 69 Beispiel eines aktiven Zweipols.

Wir möchten diesen Teil des Netzwerks als aktiven Zweipol modellieren. Zuerst bestimmen wir die Leerlaufspannung \(U_L\):

\[ U_L = \frac{R_2}{R_1 + R_2} U_0 \]

Der Kurzschlussstrom \(I_K\) ergibt sich zu:

\[ I_K = \frac{U_0}{R_1} \]

Schließlich können wir den Innenwiderstand \(R_i\) wie folgt berechnen:

\[ R_i = \frac{U_L}{I_K} = \frac{R_1 R_2}{R_1 + R_2} \]

Diese Beispiele veranschaulichen die Anwendung der Zweipol-Theorie zur Vereinfachung von Schaltungen.

DGL aus komplexen Widerständen

Die DGL und somit die Übertragungsfunktion einer elektronischen Schaltung kann auch direkt über die komplexen Widerstände bestimmt werden. Bei dem Tiefpass 1. Ordnung handelt es sich beispielsweise um die Reihenschaltung von Widerstand und Kondensator. Die komplexe Ausgangsspannung wird über dem Kondensator abgegriffen, das heißt es gilt das ohm’sche Gesetz für komplexe Zahlen. \(\underline Z_C = \frac{1}{j\omega C}\) ist die Impedanz des Kondensators mit Kapazität \(C\) und \(\underline I\) der Strom.

\[\underline U_\mathrm a = \underline Z_C \cdot \underline I\]

Die komplexe Eingangsspannung liegt am gesamten Messsystem, also der Reihenschaltung an, d.h. es gilt

\[\underline U_\mathrm e = (R+ \underline Z_C) \cdot \underline I\]

Die Division der beiden Spannungen führt abermals zur der gesuchten Übertragungsfunktion:

\[G(j \omega) = \frac{\underline U_\mathrm a}{\underline U_\mathrm e} = \frac{1/(j\omega C)}{R + 1/(j\omega C)} = \frac{1}{1+RC j \omega}\]

Die Zeitkonstante \(\tau = RC\) könnte nun noch in die Gleichung eingesetzt werden.