Einheiten#
In der Messtechnik sind Einheiten und die Kalibrierung von entscheidender Bedeutung, um präzise und reproduzierbare Messergebnisse zu erzielen. Einheiten sind die Grundlage, auf der alle Messungen beruhen, und gewährleisten, dass die gemessenen Werte weltweit verständlich und vergleichbar sind. Die Kalibrierung, als Prozess der Überprüfung und Justierung von Messgeräten, stellt sicher, dass diese Geräte genaue Messungen liefern, die den festgelegten Standards entsprechen.
Es ist sehr beruhigend, dass meine Rechenfehler mich höchstens einen Klausurversuch und Ärger beim Protokollieren kosten… noch…
—Kommentar von gwendolynneko4070 “Peinliche Rechenfehler in der Raumfahrtgeschichte”
Fehler bei der Wahl der richtigen Einheiten oder eine unsachgemäße Kalibrierung können gravierende Folgen haben, wie selbst Beispiele aus der Raumfahrtgeschichte zeigen. Selbst kleinste Ungenauigkeiten können in sensiblen Anwendungen, wie der Konstruktion von Bauwerken oder der Durchführung von wissenschaftlichen Experimenten, zu erheblichen Abweichungen und letztlich zu Misserfolgen führen. Es ist noch gar nicht so lange her, dass hohe Kosten entstanden und Raumfahrtmissionen gescheitert sind, weil falsche Einheiten oder falsche Formelzeichen bei der NASA abgetippt worden sind.
Die Bedeutung von Einheiten und Kalibrierung zeigt sich nicht nur in der modernen Technik, sondern hat auch historische Wurzeln. Ein bemerkenswertes Beispiel ist der Bau der Cheops-Pyramide, bei dem die Ägypter durch die Verwendung von standardisierten Maßeinheiten und regelmäßige Kalibrierung eine beeindruckende Präzision erreichten. Diese historischen Methoden verdeutlichen, dass genaue Messungen seit jeher ein unverzichtbarer Bestandteil technischer Meisterleistungen sind.
Dieses Kapitel wird sich mit den Grundlagen von Einheiten und Kalibrierung befassen, um ein Verständnis für deren Bedeutung und Anwendung in der Messtechnik zu schaffen.
Wunder an Präzision (2600 v. Chr.): Cheops-Pyramide
Die Cheops-Pyramide, die älteste und größte der Pyramiden von Gizeh, beeindruckt bis heute durch ihre außergewöhnliche Präzision. Erbaut vor über 4600 Jahren (2600 v. Chr.), ist sie ein Meisterwerk antiker Baukunst. Mit einer Basislänge von 230,33 Metern und einer Abweichung von weniger als 0,06 % zwischen den Seitenlängen zeugt sie von der herausragenden Messtechnik der Ägypter. Sie ist genau nach den vier Himmelsrichtungen ausgerichtet und der Unterschied in den Längen ihrer vier Seiten beträgt weniger als ein Promille! Ihre Einmessung wurde in sehr hoher Genauigkeit vorgenommen, welches in nachfolgenden Bauten nicht mehr erreicht wurde.
Drei entscheidende Parameter bestimmten die Präzision des Baus: die waagrechte Ausrichtung, die Orientierung nach den Himmelsrichtungen und die Seitenneigung. Alle drei Parameter müssen nicht nur bei Baubeginn exakt festgelegt, sondern vor allem auch während des Baus kontinuierlich kontrolliert und nachgemessen werden, sonst wird das ganze Bauwerk sichtbar unregelmäßig. Bei der enormen Höhe der großen Pyramiden von Gizeh würde ein sich wiederholender Messfehler von wenigen Millimetern nach oben hin multipliziert. Die Ägypter verwendeten standardisierte Maßeinheiten, wie die „königliche Elle“, und kalibrierten ihre Messgeräte regelmäßig, um die Genauigkeit zu gewährleisten. Fehler bei der Kalibrierung hatten schwerwiegende Konsequenzen.
Dieses hohe Maß an Genauigkeit, das mit einfachsten (steinzeitlichen) Werkzeugen und Methoden erreicht wurde, ist ein beeindruckendes Zeugnis der damaligen technischen und mathematischen Fähigkeiten.
Entwicklung des Einheitensystems#
Die frühen Ägypter verwendeten Körpermaße wie die Elle und den Fuß, die im Alltag weit verbreitet waren. Für den Bau monumentaler Strukturen wie der Pyramiden benötigten sie jedoch standardisierte und reproduzierbare Maßeinheiten. Hierfür wurden Längennormale aus Holz geschaffen, die regelmäßig mit der „königlichen Elle“ – einem Primärnormal aus Granit, das der Unterarmlänge des Pharaos entsprach – kalibriert wurden. Diese Praxis war entscheidend für die Präzision der Pyramiden, bei denen die Abweichungen zwischen den Kantenlängen der Basis lediglich 0,06 % betrugen. Dieses Verfahren zur Sicherung der Präzision erwies sich als äußerst effektiv, denn eine Fahrlässigkeit bei der Kalibrierung hatte schwerwiegende Konsequenzen, die mit dem Tod bestraft wurden.
Show code cell source
laenge_pyramide = 230.33 # in m
abweichung = 0.14 # in m
relative_abweichung = abweichung / laenge_pyramide
print('relative Messabweichung der Cheops-Pyramide: ', relative_abweichung*100, '%')
relative Messabweichung der Cheops-Pyramide: 0.06078235575044501 %
Im Laufe der Jahrhunderte entwickelten verschiedene Kulturen eigene Maßeinheiten. So führten die Griechen das Stadion (die Länge, die ein geübter Läufer schnell zurücklegen kann, etwa \(180\,\mathrm m\)) ein, während die Römer die Meile etablierten. In England wurden im 12. Jahrhundert der Yard und der Zoll basierend auf Körpermaßen eingeführt. Der Mathematiker J. Kölbel schlägt an Stelle eines Körpermaßes ein sogenanntes Naturmaß vor: “16 Männer groß und klein”, die nach einer Messe der Reihe nach aus der Kirche kommen, stellen ihre Füße hintereinander. Der sechzehnte Teil der Gesamtlänge soll dann ein Fuß sein. Diese Vielfalt an regionalen und teils willkürlichen Einheiten führte bis ins 18. Jahrhundert zu erheblichen Schwierigkeiten im Handel, in der Wissenschaft und in der Kommunikation.
Die unübersichtliche Situation, bei der jede Region eigene Einheiten nutzte, erschwerte die internationale Zusammenarbeit und den wissenschaftlichen Fortschritt. Um diesem Chaos entgegenzuwirken, wurde das Internationale Einheitensystem (SI) entwickelt. Dieses System basiert auf festen Naturkonstanten und bildet eine weltweit akzeptierte Grundlage für präzise und zuverlässige Messungen, die in Forschung, Technik und Handel unerlässlich sind.
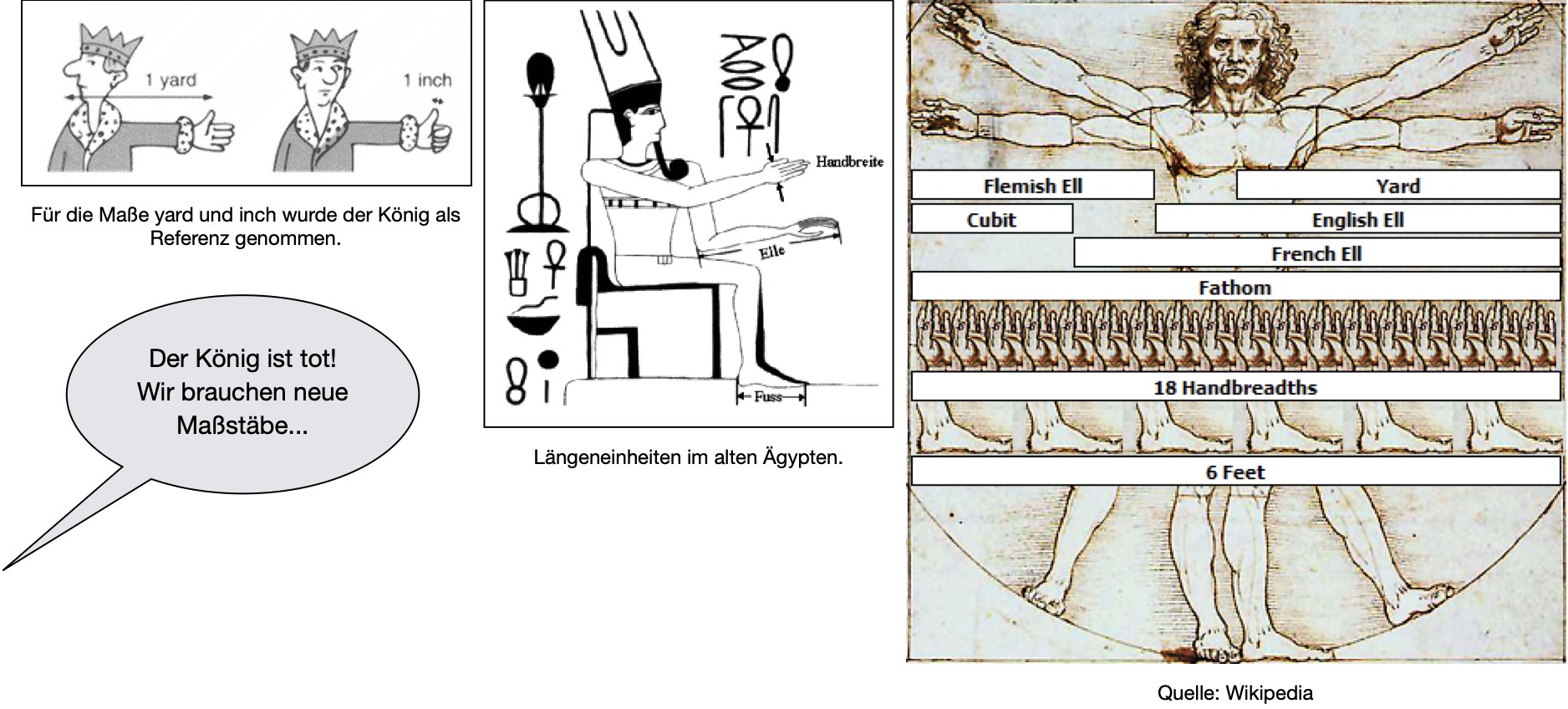
Abb. 4 Maßstäbe in der Vergangenheit.#
Während der französischen Revolution setzte die Nationalversammlung ein ehrgeiziges Ziel: die Schaffung eines neuen, universellen Einheitensystems unter dem Motto „À tous les temps, à tous les peuples“ (Für alle Zeiten, für alle Völker). Am 7. Oktober 1790 wurde der erste Antrag zur Definition des Meters eingereicht. Dieser sah vor, den Meter als den zehnmillionsten Teil der Entfernung vom Nordpol zum Äquator über Paris zu definieren. Eine Kommission aus namhaften Gelehrten, darunter Borda, Condorcet, Lagrange, Laplace und Monge, legte zwei grundlegende Maßeinheiten fest:
Der Meter sollte als universelle Längeneinheit den zehnmillionsten Teil des Erdmeridianquadranten darstellen.
Das Kilogramm sollte als universelle Masseeinheit der Masse eines Kubikdezimeters Wasser entsprechen.
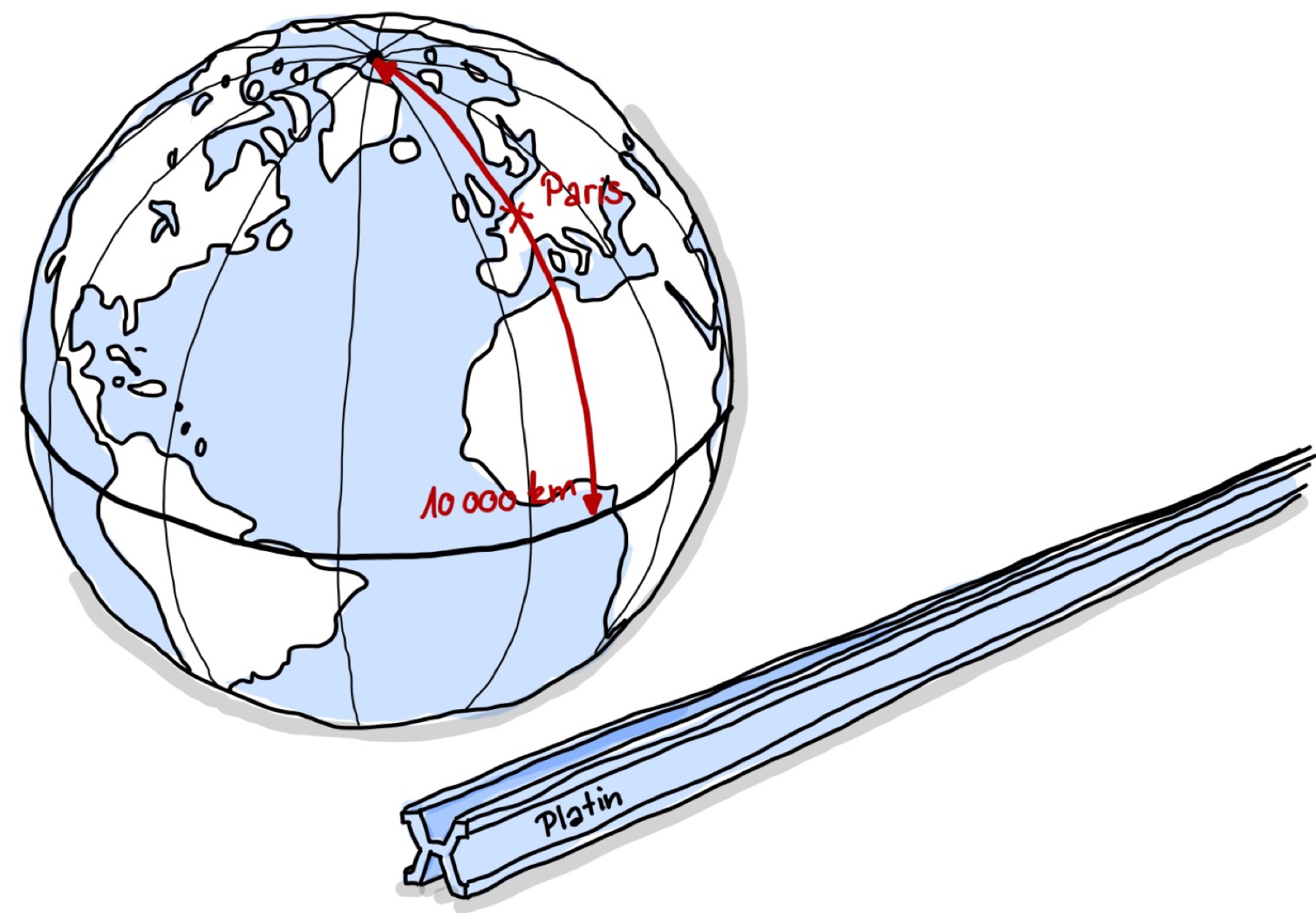
Abb. 5 Die anfängliche Definition des Meters.#
1799 wurde das naturbasierte Meter aufgrund der Komplexität seiner Bestimmung durch eine künstliche Einheit ersetzt. Ein Platinmaßstab wurde gefertigt und als „Urmeter“ in Paris aufbewahrt. 1889 wurde dieser durch einen Platin-Iridium-Stab mit X-förmigem Querschnitt ersetzt, der 90 % Platin und 10 % Iridium enthielt. Zwei Mittelstriche auf diesem Stab markierten den Meter. Bei Temperaturänderungen von 0°C auf 20°C veränderte sich die Länge des „Meters“ um 0,3 mm, wobei die Messgenauigkeit bei 0,01 mm lag.
SI-Einheiten - “The big 7”#
Im Rahmen der Meterkonvention im Jahr 1960 wurde das Internationale Einheitensystem, kurz SI, benannt nach „le Système Internationale d’unités“, eingeführt. Dies ist das am weitesten verbreitete Einheitensystem und beruht auf den 7 Basisgrößen:
Meter (m) als Einheit für die Länge
Kilogramm (kg) als Einheit für die Masse
Sekunde (s) als Einheit für die Zeit
Ampere (A) als Einheit für die elektrische Stromstärke
Kelvin (K) als Einheit für die thermodynamische Temperatur
Candela (Cd) als Einheit für die Lichtstärke und
Mol (mol) als Einheit für die Stoffmenge
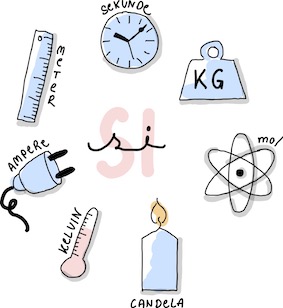
Abb. 6 Die sieben SI-Einheiten.#
Diese sieben Basisgrößen bilden die Grundlage des SI-Systems, aus denen alle weiteren Einheiten abgeleitet werden können. Das SI-System folgt dabei klaren Prinzipien, um Missverständnisse im Umgang mit physikalischen Größen zu vermeiden:
Es handelt sich um ein metrisches System, bei dem das Meter die grundlegende Längeneinheit darstellt.
Das System ist dezimal, was bedeutet, dass sich die Einheiten in 10er-Potenzen unterscheiden.
Es ist ein kohärentes System, bei dem alle Einheiten direkt aus den Basiseinheiten abgeleitet werden können.
Die Definitionen der Basiseinheiten basierten lange Zeit teilweise auf physischen Prototypen. Ein prominentes Beispiel ist das Kilogramm, das bis 2019 durch ein materielles Referenzobjekt definiert wurde. Seit 2019 werden alle SI-Einheiten von Naturkonstanten abgeleitet. Dies zeichnet sich dadurch aus, dass sie unabhängig von Ort und Zeit sind. Wenn wir die Dimensionen der festgelegten Konstanten betrachten, ergibt sich automatisch ein Zusammenhang zwischen der Konstanten und der Einheit. Das SI-System wird durch ein System von Zahlen mit präzise festgelegten Werten definiert.
Die Sekunde ist ab sofort dadurch definiert, dass die Frequenz der Cäsium-Strahlung, \(\Delta \nu_\mathrm{133Cs}\), exakt den Wert \(9{,}192631770\) annimmt, wenn man diese in \(\mathrm{1/s}\) ausdrückt (Cäsiumuhren haben übrigens eine Störanfälligkeit von \(1:10^{13}\), das entspricht einer Abweichung von \(\mathrm{1\,s}\) in \(\mathrm{300000}\) Jahren.):
\[1\,\mathrm{s} = \frac{9192631770}{\Delta \nu_\mathrm{133Cs}}\]Das Meter wird über die Lichtgeschwindigkeit \(c\) ausgedrückt. Wir kennen den Zahlenwert der Lichtgeschwindigkeit und wissen, dass sich elektromagnetische Strahlung im Vakuum immer gleich schnell ausbreitet, nämlich \(c = 299792458\,\mathrm{m/s}\). Dadurch können wir bestimmen, wie weit sich Licht in \(\mathrm{\frac{1}{299792458}\,s}\) ausbreitet. Dies bestimmt die Länge des Meters:
\[1\,\mathrm{m} = \frac{c}{299792458}\,\mathrm{s} = 30{,}663318...\frac{c}{\Delta \nu_\mathrm{133Cs}}\]Das Kilogramm ist nun durch Ableitung aus dem Planckschen Wirkungsquantum \(h = 6{,}62607015 \cdot 10^{-34}\,\mathrm{Js}\) definiert, wobei die Einheit \(\mathrm{J} \) (Joule), wie unten noch aufgeführt wird, nichts anderes als \(\mathrm{kg\,m^2/s^2}\) ist. \(h\) wird dabei in Kooperation der metrologischen Institutionen in Form aufwendiger Experimente in entsprechender Genauigkeit bestimmt. Wie schwer ein Kilogramm ist, misst die Watt-Waage mittels einer elektromagnetischen Kraft durch das Ausgleichen der Gewichtskraft.
\[1\,\mathrm{kg} = \frac{h}{6{,}626070040 \cdot 10^{-34}}\,\mathrm{m^{−2}\,s} = 1{,}475521... \cdot 10^{40}\,h \cdot \frac{\Delta \nu_\mathrm{133Cs}}{c}\]Das Kelvin ist die Einheit der thermodynamischen Temperatur, über die Boltzmann-Konstante \(k_B = 1{,}38064852 \cdot 10^{-23}\,\mathrm{kg\,m^2\,s^{-2}\,K^{-1}}\). Im Alltag benutzen wir die davon abgeleitete Einheit \(\mathrm{^\circ C}\). \(0\,\mathrm{K}\) entsprechen \(-273{,}15\,\mathrm{K}\) und drücken den absoluten Temperaturnullpunkt aus.
Das Ampere wird dadurch definiert, dass die Elementarladung \(e = 1{,}6021766208 \cdot 10^{-19}\,\mathrm{As}\) beträgt. Im Experiment wird zur Bestimmung des Ampere \(e\) benutzt und im Stromfluss die Anzahl der Elektronen pro Sekunde gemessen.
Die Basisgrößen für Licht und Stoffmenge begegnen uns im Alltag nicht so häufig und werden meist von Wissenschaftlern verwendet.
Das Mol ist dadurch definiert, dass die Avogadro-Konstante \(N_A = 6{,}022140857 \cdot 10^{23}\,\mathrm{mol^{-1}}\) beträgt. \(N_A\) ist die Zahl, der in einem Mol enthaltenen Atome. Sie ist so definiert, dass \(\mathrm{12\,g}\) Kohlenstoff \(\mathrm{12C}\) genau einem Mol entspricht.
Die Candela wird vom photometrischen Strahlungsäquivalent \(\mathrm K_\mathrm{cd}\) (ebenfalls eine Naturkonstante) abgeleitet. Sie wird über die SI-Einheiten \(\mathrm{kg}\), \(\mathrm{m}\), \(\mathrm{s}\) und Steradiant (sr = \(\mathrm{m^2/m^2}\)) definiert.
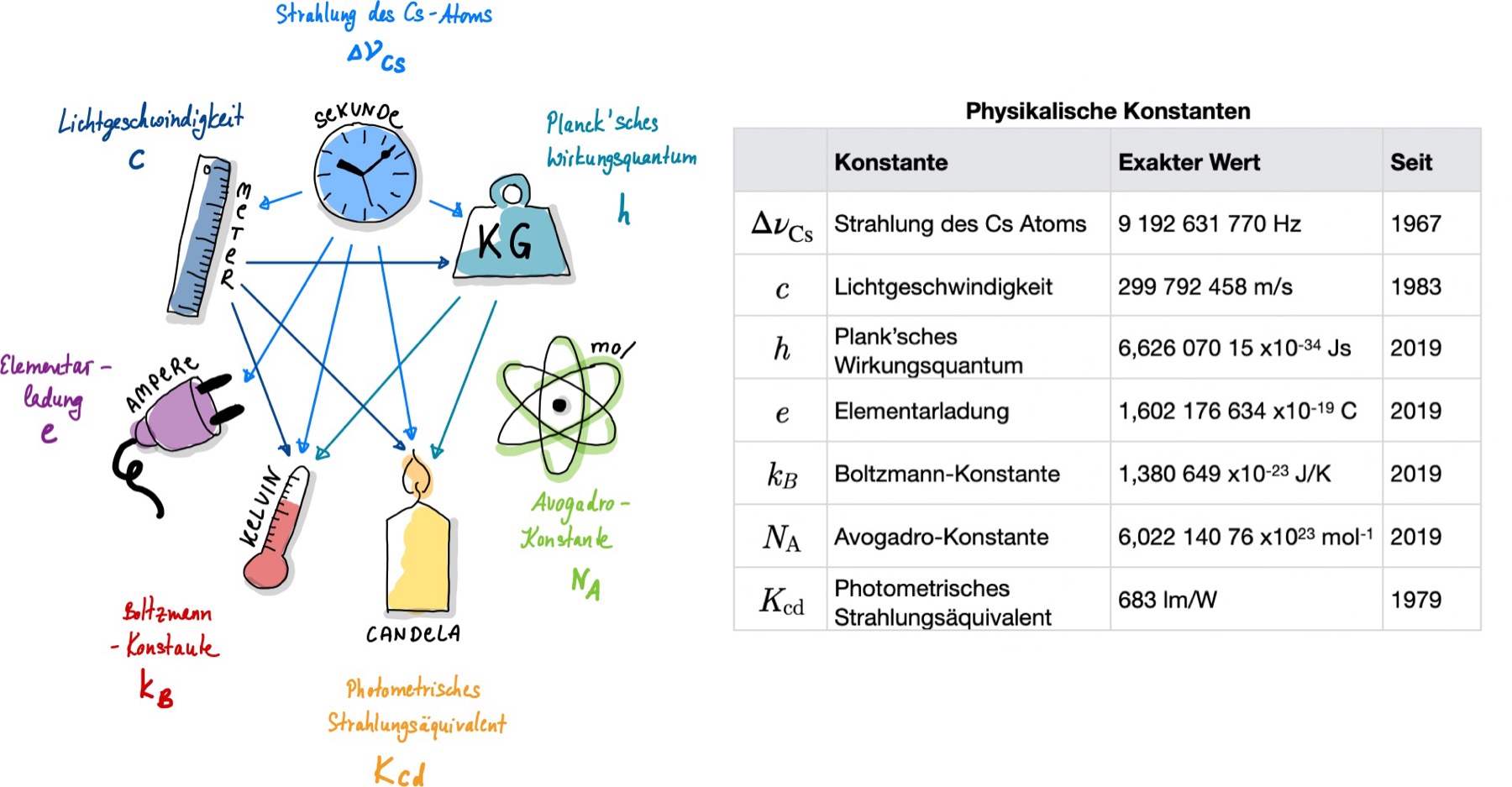
Abb. 7 Die Definition der SI-Einheiten mittels Naturkonstanten und wie sich diese voneinander ableiten.#
Diese Einheiten bilden die Grundlage für die Messung aller anderen physikalischen Größen. Geschwindigkeit, Beschleunigung und alles, was wir messen, leitet sich von diesen Basiseinheiten ab.
Beispiel: Definition des Kilogramms#
Watt-Waage
Die Definitionen der Basiseinheiten basierten lange Zeit teilweise auf physischen Prototypen, wobei das Kilogramm eine besondere Rolle spielte. Von 1889 bis 2018 war das Kilogramm durch einen Metallzylinder aus 90 % Platin und 10 % Iridium, bekannt als das “Ur-Kilogramm”, definiert. Dieser Zylinder, \(\mathrm{3{,}9\,cm}\) hoch und \(\mathrm{3{,}9\,cm}\) im Durchmesser, wurde unter drei Glasglocken in einem Tresor des „Internationalen Büros für Maß und Gewicht“ (BIPM) in Paris aufbewahrt. Im Laufe der Zeit stellte sich jedoch heraus, dass das Ur-Kilo allmählich an Masse verlor – etwa \(\mathrm{50\,\mu g}\) in \(\mathrm{129}\) Jahren – was in unserer modernen, hochpräzisen Welt zunehmend problematisch wurde.
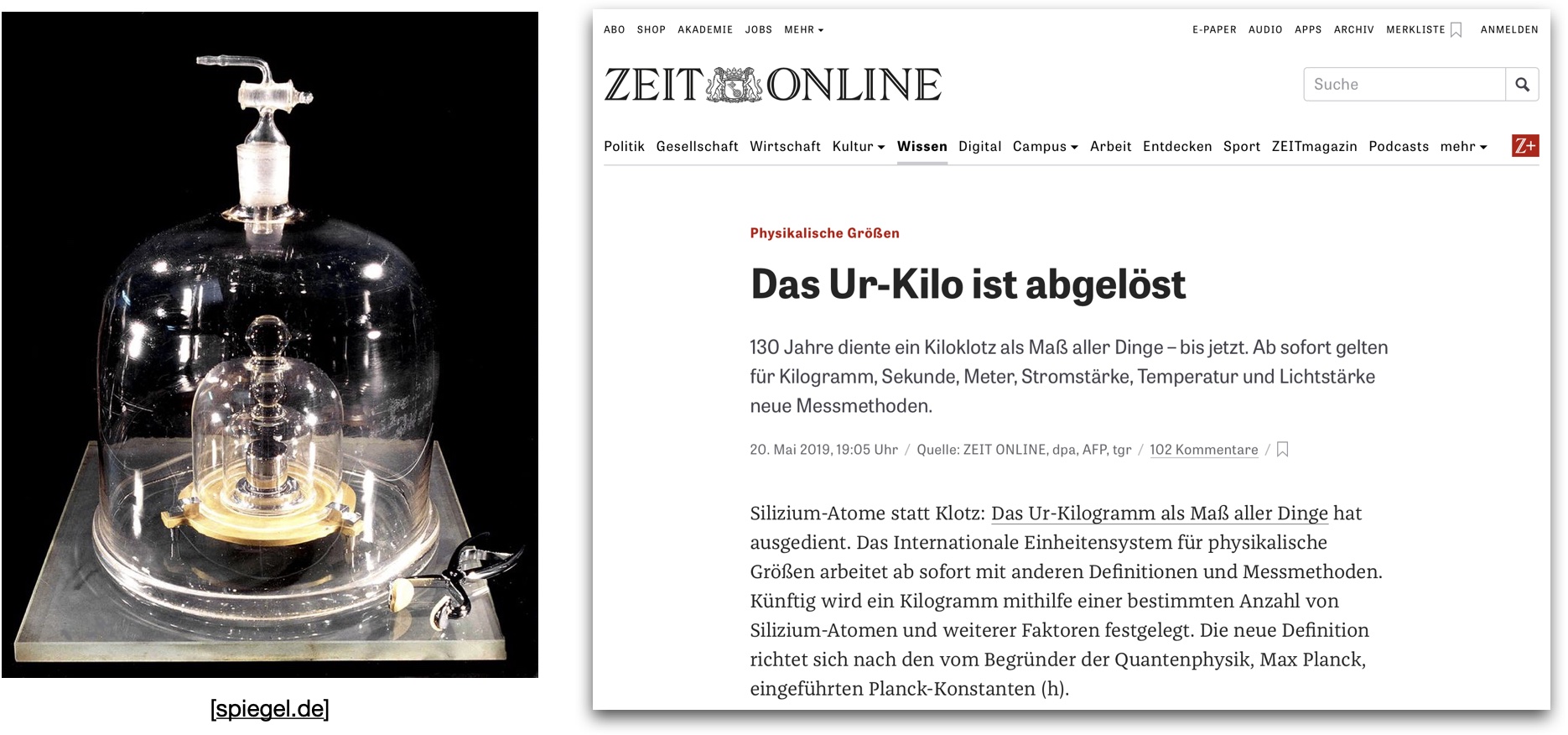
Abb. 8 Bericht zur Ablösung des Ur-Kilogramms.#
Um dieses Problem zu lösen, wurde das Kilogramm 2019 neu definiert, basierend auf der Planck-Konstanten \(h\), die einen festen Wert von \(6{,}62607015 \times 10^{-34}\,\mathrm{Js}\) erhielt. Diese Neudefinition erfolgt durch die Verwendung der sogenannten Watt-Waage (auch Kibble-Waage genannt). Dieses hochpräzise Instrument misst die Leistung, die erforderlich ist, um eine bekannte Masse gegen die Schwerkraft anzuheben, und nutzt dabei die Planck-Konstante zur Berechnung der Masse.
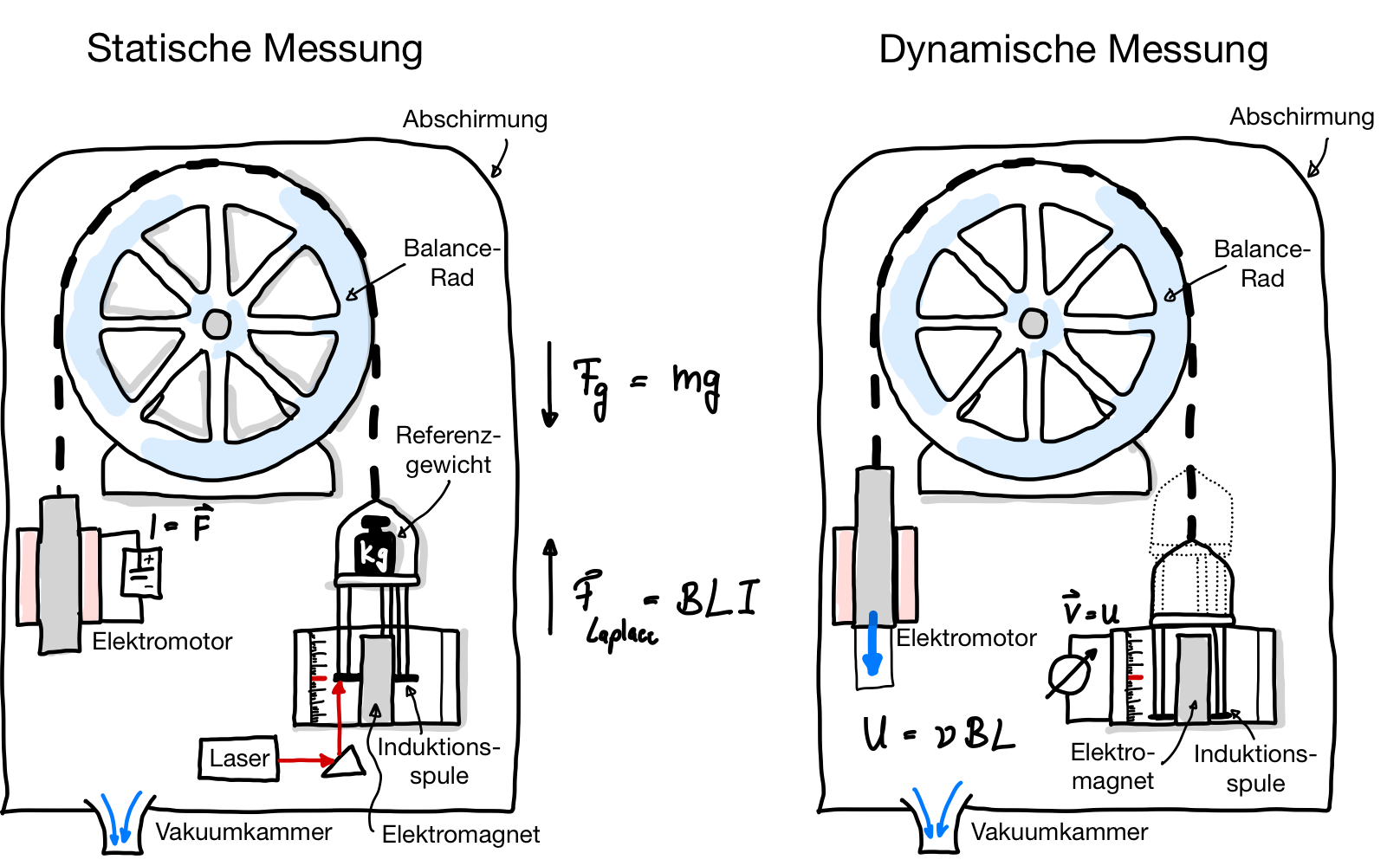
Abb. 9 Schematische Darstellung des Funktionsprinzips der Wattwaage. .#
Die Watt-Waage funktioniert nach folgendem Prinzip: Statt zwei Massen direkt miteinander zu vergleichen, wie es bei einer herkömmlichen Waage der Fall ist, wird die Masse eines Objektes mit einer elektromagnetischen Kraft ausgeglichen. Dabei wird auf einer Seite der Waage eine Masse \(m\) platziert, die aufgrund der Gravitationskraft \(F_G\) nach unten wirkt. Auf der anderen Seite der Waage erzeugt eine Spule aus Draht, mit der Länge \(L\), die sich frei über einem Magneten bewegen kann, eine elektromagnetische Kraft, wenn ein Strom \(I\) durch die Spule fließt und ein Magnetfeld \(B\) erzeugt wird. Diese erzeugte Kraft, die sogenannte Laplace-Kraft \(F_\mathrm{Laplace}\), balanciert die Waage aus, wenn \(F_G = F_\mathrm{Laplace}\) gilt:
Da \(B\) und \(L\) in der Praxis schwer exakt zu messen sind, nutzt die Watt-Waage einen Trick: Statt die Werte direkt zu messen, wird die Spule mit einer bestimmten Geschwindigkeit \(v\) durch das Magnetfeld bewegt, wodurch nach Faradayschem Induktionsgesetz eine Spannung \(U_\mathrm{ind}\) induziert wird:
Durch diesen Ansatz müssen \(B\) und \(L\) nicht direkt gemessen werden. Stattdessen werden nur die induzierte Spannung \(U_\mathrm{ind}\) und die Geschwindigkeit \(v\) gemessen, was mit hoher Präzision möglich ist. Die Spannung kann über den Quanten-Hall-Effekt und die Josephson-Spannung extrem genau bestimmt werden, während die Geschwindigkeit mit laserinterferometrischen Sensoren gemessen wird. Dadurch ergibt sich für die Leistung:
Daraus lässt sich die Masse \(m\) berechnen:
Der Name Watt-Waage leitet sich aus dem Prinzip ab, dass hier zwei Leistungen (Watt) miteinander verglichen werden: die mechanische Leistung \(mgv\) und die elektrische Leistung \(U_\mathrm{ind} I\). Mit dieser Methode wurde das Kilogramm von einem physischen Objekt auf eine fundamentale Naturkonstante umgestellt, was eine präzise und weltweit reproduzierbare Masseinheit garantiert.
Abgeleitete / Ergänzende SI-Einheiten#
SI umfasst auch eine Aufzählung weiterer Einheiten, welche von den 7 Basiseinheiten, oder über physikalische Gesetzmäßigkeiten, abgeleitetet werden können. Es gibt insgesamt 22 abgeleitete Einheiten, im Folgenden eine Auswahl:
1 m\(^2\) (Quadratmeter für Fläche) = 1 m\(\cdot\)m
1 Hz (Hertz für Frequenz) = 1/s
1 N (Newton für Kraft) = kgm/s\(^2\)
1 Pa (Pascal für Druck) = 1 N/m\(^2\) = 1 kg/ms\(^2\)
1 J (Joule für Energie) = 1 Nm = 1 kg\(^2\)/s\(^2\)
1 W (Watt für Leistung) = 1 J/s = 1 kgm\(^2\)/s\(^3\)
1 V (Volt für Spannung) = 1 W/A = 1 kgm\(^2\)/s\(^3\)A
1 H (Henry für Induktivität) = 1 Vs/A = 1 kgm\(^2\)/s\(^2\)A\(^2\)
1 F (Farad für Kapazität) = 1 As/V = 1 s\(^4\)A\(^2\)/kgm\(^2\)
Zwischen verschiedenen physikalischen Teildisziplinen kann nun auch mit den Einheiten hin und her jongliert werden. So kommt die Leistung (W) sowohl in mechanischen, als auch elektrischen Gesetzmäßigkeiten vor.
Ergänzende Einheiten im SI-System sind beispielsweise:
1 rad (Radiant) = 1 m/m, welches der ebene Winkel zwischen zwei Radien eines Kreises ist, falls der dadurch beschriebene Kreisbogen genauso groß ist wie der Radius. Der Umfang eines Kreises ist bekannterweise \(2\pi \cdot r\), wobei \(r\) der Kreisradius ist. Dadurch entspricht eine komplette Drehung einem Winkel von \(2\pi\,\mathrm{rad}\)
1 sr (Steradiant) = 1 m\(^2\)/m\(^2\) ist der räumliche Winkel (analog zum Radiant). Dieser schließt mit der Kugelmitte als Scheitelpunkt eine Fläche auf der Kugeloberfläche ein. Diese Fläche ist quadratisch mit einer Seitenlänge die dem Kugelradius entspricht. Die Einheit kann also ebenfalls auf Basiseinheiten zurückgeführt werden, hier 1 sr = m\(^2\)/m\(^2\).
Nicht-SI-Einheiten (Akzeptierte Einheiten)#
Es gibt diverse zusätzliche Einheiten, welche keine offiziellen SI-Einheiten sind, aber aufgrund ihrer großen Beliebtheit und Handhabbarkeit gerne benutzt werden. Im Allgemeinen gibt es aber immer Zusammenhänge zu den SI-Einheiten, sodass sie sich in solche umformen lassen. Beispiele sind z.B.:
Grad Celsius: 1°C = K + 273,15
Grad Fahrenheit: 1°F = 9/5 K - 459,67
Minute: 1 min = 60 s
(Winkel-)Grad: 1° = \(\pi\)/180 rad
(Winkel-)Minute: 1’ 1/60°
Liter: 1 l = 1 dm\(^3\)
Tonne: 1 t = 10\(^3\) kg
Bar: 1 bar = 10\(^5\) Pa
Dann gibt es noch historisch gewachsene Einheiten, wie z.B. die Meile, yard, foot, inch, once, pound, gallon, welche sich analog in SI-Einheiten umrechnen lassen. Diese Umrechnung ist global nicht immer die gleiche und es existieren für dieselbe Einheit unterschiedliche Umrechnungen (USA und UK sind hier die wohl bekanntesten Beispiele). Doch auch je nach Anwendungsgebiet gibt es Unterschiede:
1 mile = 1 Landmeile = 1.609,344 m (US)
1 nautical mile = 1 Seemeile (oder Luftfahrt) = 1.853,2 m (UK)
1 mile = exakt 1.852 m (international)
Einheiten, die zwar in Gebrauch sind, aber nicht auf SI-Einheiten zurückzuführen sind, wurden für spezifische Einsatzgebiete konkret festgelegt:
die Wasserhärte
das Mostgewicht
den Feingehalt von Gold- und Silberlegierungen
die Windstärke
den Seegang
die Stärke von Erdbeben
Vorsätze und Präfix im SI#
Zum SI, bzw. prinzipiell angewendet in allen anderen Einheiten, sind sogenannte Präfixe / Vorsätze definiert. Teile oder Vielfache von SI-Einheiten können in Kurzform geschrieben werden, was das Lesen erleichtert. So können besonders große oder besonders kleine Zahlen übersichtlicher dargestellt werden. Dafür muss der oder die Forschende oder Ingeneur:in lediglich ein paar Vokabeln können.
Zeichen |
Name |
Multiplikator |
|---|---|---|
Y |
Yotta |
\(10^{24}\) |
Z |
Zetta |
\(10^{21}\) |
E |
Exa |
\(10^{18}\) |
P |
Peta |
\(10^{15}\) |
T |
Tera |
\(10^{12}\) |
G |
Giga |
\(10^{9}\) |
M |
Mega |
\(10^{6}\) |
k |
Kilo |
\(10^{3}\) |
h |
Hekto |
\(10^{2}\) |
da |
Deka |
\(10^{1}\) |
Zeichen |
Name |
Multiplikator |
|---|---|---|
d |
Dezi |
\(10^{-1}\) |
c |
Zenti |
\(10^{-2}\) |
m |
Milli |
\(10^{-3}\) |
μ |
Mikro |
\(10^{-6}\) |
n |
Nano |
\(10^{-9}\) |
p |
Pico |
\(10^{-12}\) |
f |
Femto |
\(10^{-15}\) |
a |
Atto |
\(10^{-18}\) |
z |
Zepto |
\(10^{-21}\) |
y |
Yokto |
\(10^{-24}\) |
Logarithmische Einheiten#
In der Messtechnik können Messwerte in sehr unterschiedlichen Größenordnungen auftreten. Wir haben bereits im vorherigen Kapitel die Präfixe und Vorsätze betrachtet, um diese Vielfalt zu handhaben. Dennoch kann es schwierig sein, die gesamte Messreihe übersichtlich auf einem Diagramm darzustellen, da die Achsen normalerweise feste Einheiten haben. Aus diesem Grund greifen wir oft auf die logarithmische Darstellung zurück, obwohl sie auf den ersten Blick komplex erscheinen mag. Diese Methode bietet jedoch erhebliche Vorteile und ist auch im Rahmen des SI-Systems anerkannt.
Im folgenden Diagramm ist die Funktion
gezeichnet.
Show code cell source
import scipy.signal as signal
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
import seaborn as sns
import time
import warnings
warnings.filterwarnings('ignore')
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
plt.figure(figsize=(8,5)) # Plot-Größe
plt.rcParams['font.size'] = 10; # Schriftgröße
def f(x):
return 2*np.log10(x)
# Daten:
x = np.logspace(-1,3,200)
data = {"frequenz": x, "amplitude_V":f(x), "amplitude_dB": 20*np.log(f(x))}
data_df = pd.DataFrame(data)
#data_df["amplitude_V"] = 10**(data_df["amplitude"]/20)
plt.subplot(2,2,1)
plt.plot(data_df["frequenz"], data_df["amplitude_V"])
#plt.fill_between(data_df["frequenz"],data_df["amplitude_V"],0,color='tab:blue', alpha=0.2)
plt.ylabel("y")
plt.xlabel("x")
plt.text(200,2,r'$f(x) = 2\cdot \log(x)$')
plt.title('Lineare Achsen')
plt.subplot(2,2,3)
plt.semilogx(data_df["frequenz"], data_df["amplitude_V"])
#plt.fill_between(data_df["frequenz"],data_df["amplitude_V"],0,color='tab:blue', alpha=0.2)
plt.ylabel("y")
plt.xlabel("x")
plt.text(10,0,r'$f(x) = 2\cdot \log(x)$')
plt.title('Halblogarithmisches Diagramm in x')
plt.subplot(2,2,4)
plt.plot(np.log10(data_df["frequenz"]), data_df["amplitude_V"])
#plt.fill_between(data_df["frequenz"],data_df["amplitude_V"],0,color='tab:blue', alpha=0.2)
plt.ylabel("y")
plt.xlabel("log(x)")
plt.text(1.7,0,r'$f(x) = 2\cdot \log(x)$')
plt.text(-0.1,-1,r'Geradenvergleich: $f(x) = m\cdot x$')
plt.title('Logarithmische x-Werte')
plt.tight_layout()
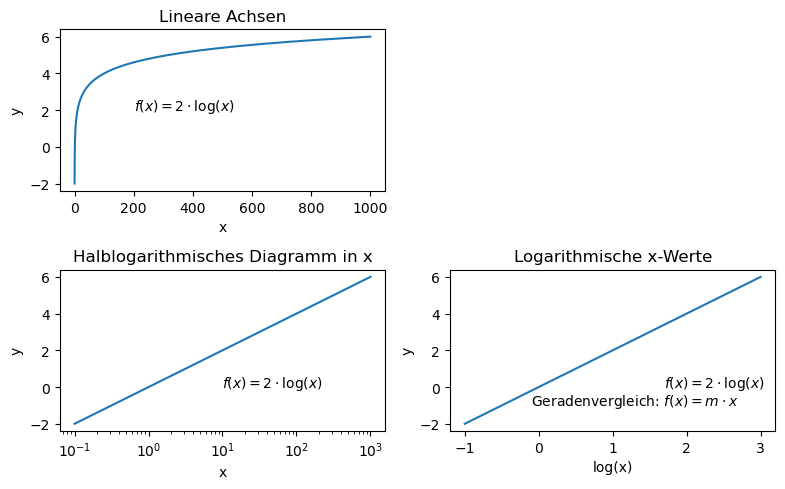
Man erkennt, dass die y-Werte mit steigendem x-Wert nur sehr langsam ansteigen. Bei x=1000 ist y = 6 und man müsste noch größere x-Werte zeichnen, um den weiteren Trend zu erkennen. Ein neues Koordinationsystem hilft in der Darstellung. Prinzipiell können der 10er oder der natürliche Logarithmus gewählt werden, dies sollte man dann aber unbedingt dazu schreiben, damit keine Verwirrung entsteht. Das Prinzip ist aber immer das gleiche:
\(\log(x)\) (neue \(x\)-Achse) |
\(10^{\log(x)}\) (Umrechnung) |
\(x\) (alte Achse) |
|---|---|---|
0 |
\(10^{0}\) |
\(\Rightarrow x = 1 \) |
1 |
\(10^{1}\) |
\(\Rightarrow x = 10 \) |
2 |
\(10^{2}\) |
\(\Rightarrow x = 100 \) |
3 |
\(10^{3}\) |
\(\Rightarrow x = 1000 \) |
… |
… |
… |
Jeder Schritt auf der x-Achse wird in der logarithmischen Darstellung nicht nur +1 mehr, sondern jeder Schritt verzehnfacht sich, wodurch die x-Achse optisch gestaucht wird.
In den folgenden Diagrammen ist einmal dargestellt, wie viel besser Koordinatensysteme ausgenutzt werden können, wenn zu einer logarithmischen Darstellung gewechselt wird. Während bei linearen Achsen nur ein ganz kleiner des Diagramms ausgenutzt wird und man kaum was erkennen kann wie die Messwerte skalieren, ist bei der doppellogarithmischen Darstellung gut zu sehen, wie sich die Messwerte verhalten.
Show code cell source
import scipy.signal as signal
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
import seaborn as sns
import time
import warnings
warnings.filterwarnings('ignore')
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.figure(figsize=(8,5)) # Plot-Größe
plt.rcParams['font.size'] = 10; # Schriftgröße
# Transfer Funktion für das Model eines Tiefpasses:
num = np.array([1])
den = np.array([1 , 1, 1])
H = signal.TransferFunction(num , den)
# Bode-Plot Daten:
w2 = np.logspace(-3,2,200)
w, mag, phase = signal.bode(H,w2)
data = {"frequenz": w, "amplitude": mag, "phase": phase}
data_df = pd.DataFrame(data)
data_df["amplitude_V"] = 10**(data_df["amplitude"]/20)
plt.subplot(2,2,1)
plt.plot(data_df["frequenz"], data_df["amplitude_V"])
plt.fill_between(data_df["frequenz"],data_df["amplitude_V"],0,color='tab:blue', alpha=0.2)
plt.ylabel("Amplitude (V)")
plt.xlabel("Frequenz (Hz)")
plt.title('Lineare Achsen')
plt.subplot(2,2,2)
plt.semilogx(data_df["frequenz"], data_df["amplitude_V"])
plt.fill_between(data_df["frequenz"],data_df["amplitude_V"],0,color='tab:blue', alpha=0.2)
plt.ylabel("Amplitude (V)")
plt.xlabel("Frequenz (Hz)")
plt.title('x-Achse logarithmisch')
plt.subplot(2,2,3)
plt.plot(data_df["frequenz"], data_df["amplitude"])
plt.fill_between(data_df["frequenz"],data_df["amplitude"],-80,color='tab:blue', alpha=0.2)
plt.ylabel("Amplitude (dB)")
plt.xlabel("Frequenz (Hz)")
plt.title('y-Achse logarithmisch: dB')
plt.subplot(2,2,4)
plt.semilogx(data_df["frequenz"], data_df["amplitude"])
plt.fill_between(data_df["frequenz"],data_df["amplitude"],-80,color='tab:blue', alpha=0.2)
plt.ylabel("Amplitude (dB)")
plt.xlabel("Frequenz (Hz)")
plt.title('Doppel-logarithmisch')
plt.tight_layout()
plt.savefig('log_plot1.png')
plt.savefig('log_plot1.pdf')
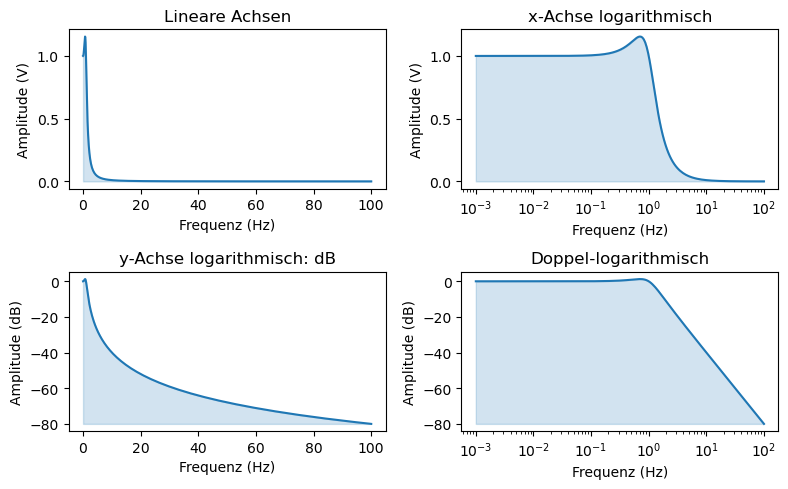
Statt einer logarithmischen Darstellung im Diagramm können Messwerte auch in die logarithmische Einheit Dezibel (dB) umgerechnet werden. Dies wir häufig bei akustischen und elektronischen Signalen verwendet, insbesondere in der Hochfrequenztechnik. Bei der Umrechnung wird der Messwert im Vergleich zu einem definierten Referenzwert bewertet, indem der Quotient aus Messwert und Referenzwert gebildet wird. Dies ergibt \(P/P_\mathrm{ref}\) für Leistungen oder \(U/U_\mathrm{ref}\) für Spannungen. Anschließend werden diese Quotienten logarithmiert, in der Regel unter Verwendung des Zehnerlogarithmus. In der Messtechnik hat sich eine ungeschriebene Regel etabliert, die besagt, dass Leistungen gemäß dieser Vorgehensweise in die Einheit dB umgewandelt werden, wobei dies als Leistungsgröße bezeichnet wird:
Hieraus kann die Umrechnung auch für sogenannten Feld- oder Amplitudengrößen hergeleitet werden. Es gilt bekanntlich für die Wirkleistung an einem Verbraucher \(R\)
Setzt man dies in die obige Umrechnungsformel ein erhält man:
Mittels der logarithmischen Rechenregel \(\log _{b}\left(x^{r}\right)=r\log _{b}x\) folgt
Der resultierende Wert ist per Definition dimensionslos, wird jedoch der Einheit “Dezibel” (dB) zugeordnet, was einem Zehntel eines “Bels” entspricht. Gelegentlich wird auch der natürliche Logarithmus verwendet, wodurch die Einheit “Neper” (Np) entsteht.
Die Rücktransformation erfolgt über folgende Gleichungen für Leistungsgrößen
und Spannungsgrößen (Feldgrößen):
Im Allgemeinen spricht man von “Pegeln”, wenn Messwerte logarithmisch ausgedrückt werden. Bei der Verwendung der Einheit Dezibel ist es unbedingt erforderlich, den Referenzwert anzugeben. Typische Schreibweisen sind beispielsweise:
dB(mW): Dies bezieht sich auf einen Leistungspegel mit einem Referenzwert von 1 mW.
dB(mV): Dies bezieht sich auf einen Spannungspegel mit einem Referenzwert von 1 mV.
dB(\(\mu\)V): Dies bezieht sich auf einen Spannungspegel mit einem Referenzwert von 1 \(\mu\)V.
Ohne Angabe des Referenzwerts sind weder die physikalische Größe noch der Skalierungsfaktor bekannt, was besonders wichtig ist, wenn der Dezibel-Wert später in absolute Einheiten zurückkonvertiert werden muss.
Für Leistungspegel gilt im Allgemeinen (bei einem typischen Referenzwert von 1 mW) 1 \(\mu\)W = 0,000001 W = -30 dB(mW).
Absolute Größen sind über einen Leistungsnormpegel von \(P_\mathrm{ref} = 1\,\mathrm{mW}\) definiert, welcher an einem Widerstand von \(R = 600\,\Omega\) abfällt und zu einem äquivalenten Spannungsnormpegel von \(U_\mathrm{ref} = 0{,}775\,\mathrm V\) führt.
Für Hochfrequenzsignale gilt der Spezialfall, dass der Widerstandswert \(R = 50\,\Omega\) angenommen wird. Das liegt daran, dass bei hoch frequenten Signalen Reflektionen in den Kabeln und Schnittstellen auftreten, weshalb häufig Messgeräte mit nierohmigen Innenwiderständen verwendet werden. Der Leistungsnormpegel bleibt bei \(P_\mathrm{ref} = 1\,\mathrm{mW}\), die reduzierte Widerstandswert führt zu einen Spannungsnormpegel von \(U_\mathrm{ref} = 0{,}224\,\mathrm V\). In diesem Speziallfall wird statt der Einheit dB die Einheit dBm verwendet (nicht zu verwechseln mit dB(mW)!).
Beispiel aus der Akustik
Unterscheide: Schalldruck \(p\) ist eine Schallfeldgröße und Schallintensität \(I\) ist eine Schallenergiegröße.
0dB bedeutet, dass sich der Ton direkt an der Grenze des menschlich hörbaren befindet.
Ein positiver dB Wert bedeutet, dass der Ton um ein Vielfaches lauter ist als die 0dB Grenze.
Ein negativer dB Wert bedeutet, dass der Ton um ein Vielfaches leister ist als die 0dB Grenze.
Aufgabe
In der folgenden Code-Cell können verschiedene Umrechnungen für Messwerte ausprobiert werden. Einfach Referenzwert \(P_\mathrm{ref}\) im Live-Code ändern, den Messwert \(P\) anpassen und beobachten, wie sich der Dezibel-Wert ändert.
Änder den Referenzwert
P_refvon 1mW auf 1W und 1\(\mu\)W.Änder den Messwert
PBeachte, dass bei der Angabe des Pegelwertes der Referenzwert immer in Klammern mitangebeben werden muss!
import numpy as np # lade numpy Library
P = 1e-6 # Messwert, hier 1 uW
P_ref = 1e-3 # Referenzwert = 1 mW
P_dB = 10 * np.log10(P/P_ref) # Achtung: in numpy ist "log" der natürlich Logarithmus ln
print('Leistungswert = %.e W = %.10f W' %(P, P))
print('Pegel in dB: ', P_dB, '(%.3f)' %(P_ref))
Leistungswert = 1e-06 W = 0.0000010000 W
Pegel in dB: -30.0 (0.001)


