Beschleunigungssensoren

Möchte man die Beschleunigung eines Objektes messen bedient man sich dem Trägheitsgesetz:

\[F = m \cdot a\]

nachdem so gut wie alle Sensoren funktionieren.

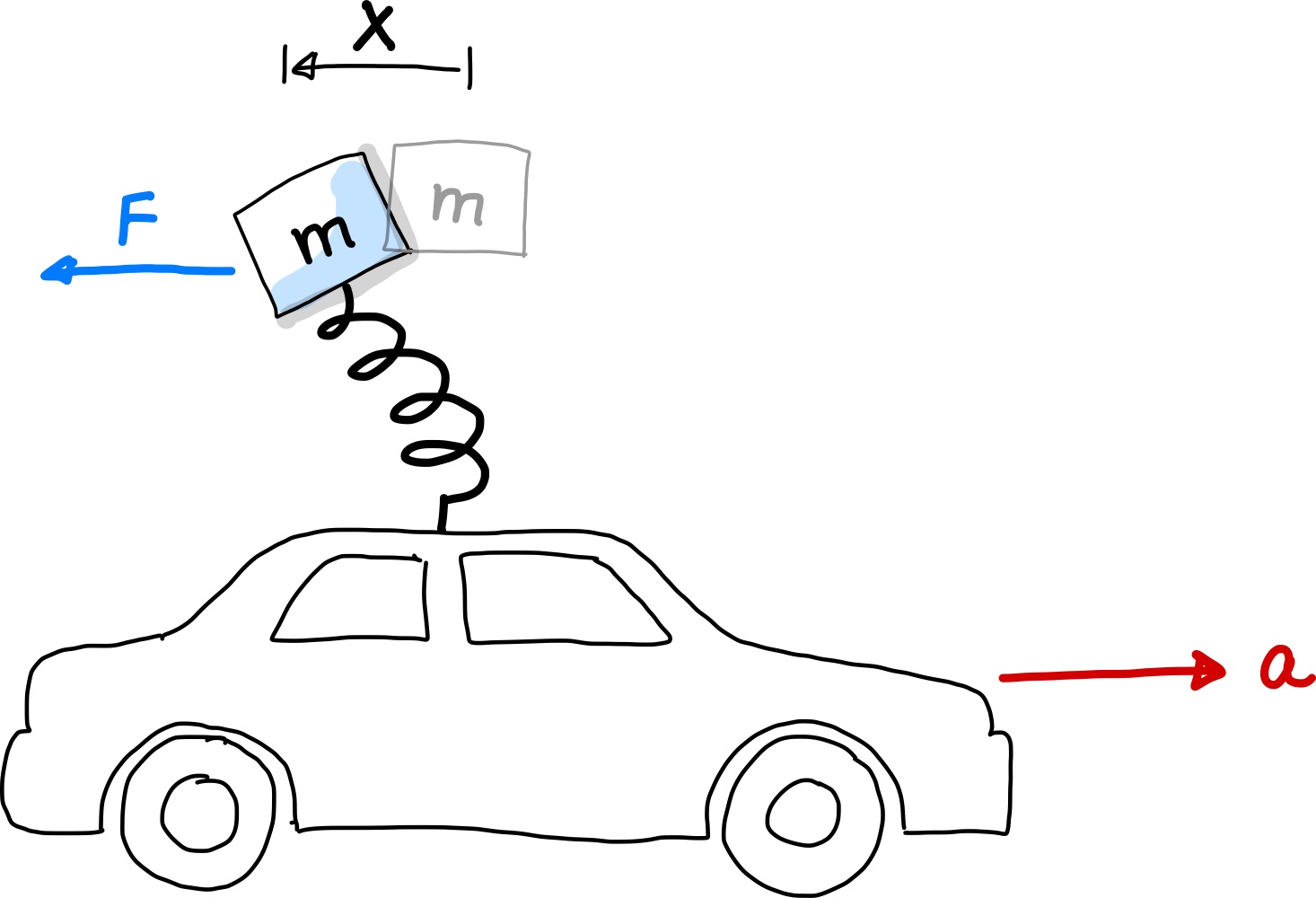
Abb. 126 Beschleunigungsmessung nach dem Trägerheitsprinzip.

Hierbei befestigt man einen kleinen Massekörper, der die Masse \(m\) trägt, an einer Feder an das Sensorgehäuse oder dem Objekt, dessen Beschleunigung man messen möchte:

\[a = \frac{F}{m}\]

Häufig wird jedoch nicht die Kraft gemessen, was mittels Dehnungsmesstreifen oder Piezoelektrischem Sensor möglich ist, sondern die Auslenkung der Feder \(x\):

\[x = k \cdot F\]

wobei \(k\) die Federkonstante ist. Die auslenkung \(x\) kann mit den bisher besprochenen Techniken zur Abstandsmessung im Kapitel zu Kapazitiven und Induktiven Sensoren gemessen werden oder optisch mittels Interferometrie erfolgen.

Kapazitive Beschleunigungssensoren

Kapazitive Auslesetechniken sind in der Herstellung sehr einfach und werden daher am häufigsten verwendet. Die Messsyteme können dadurch auch sehr klein werden, weshalb kapazitive Sensoren gerne in MEMS (micro-electro-mechanical systems) Technologie zum Einsatz kommt. D.h. sie haben eine Größe von wenigen Hundert Mikrometern!

Hierbei misst man die Kapazitätsänderung eines Kondensatoranordnung, die an einer Feder aufgehängten sind, gegenüber einer fixierten Kondensatoranordnung. Hierbei wird ausgenutzt, dass sich die Kapazität in Abhängigkeit der Kondensatorplattenabstände ändert.

\[\Delta C = C_2 - C_1\]

Aufgrund einer externen Beschleunigung erfahren die aufgehängten Kondensatorplatten eine Positionsänderung \(\Delta d\) gegenüber der festinstallierten und die Kapazität ändert sich.

\[\Delta C = \epsilon_0 \frac{A}{d \pm \Delta d} - \epsilon_0 \frac{A}{d} = \frac{\mp \epsilon_0 A \Delta d}{d (d \pm \Delta d)} = \mp C_1 \frac{\Delta d}{d \pm \Delta d}\]

Die Kapazitätsänderung wird wieder mittels einer Brückenschaltung gemessen. Um das System zu linearisieren wird eine Differentialanordnung ausgewählt. Dieses Messprinzip erlaubt eine Temperaturkompensation. In Abb. 127 ist eine solche Abbildung inklusive Brückenschaltung dargestellt.

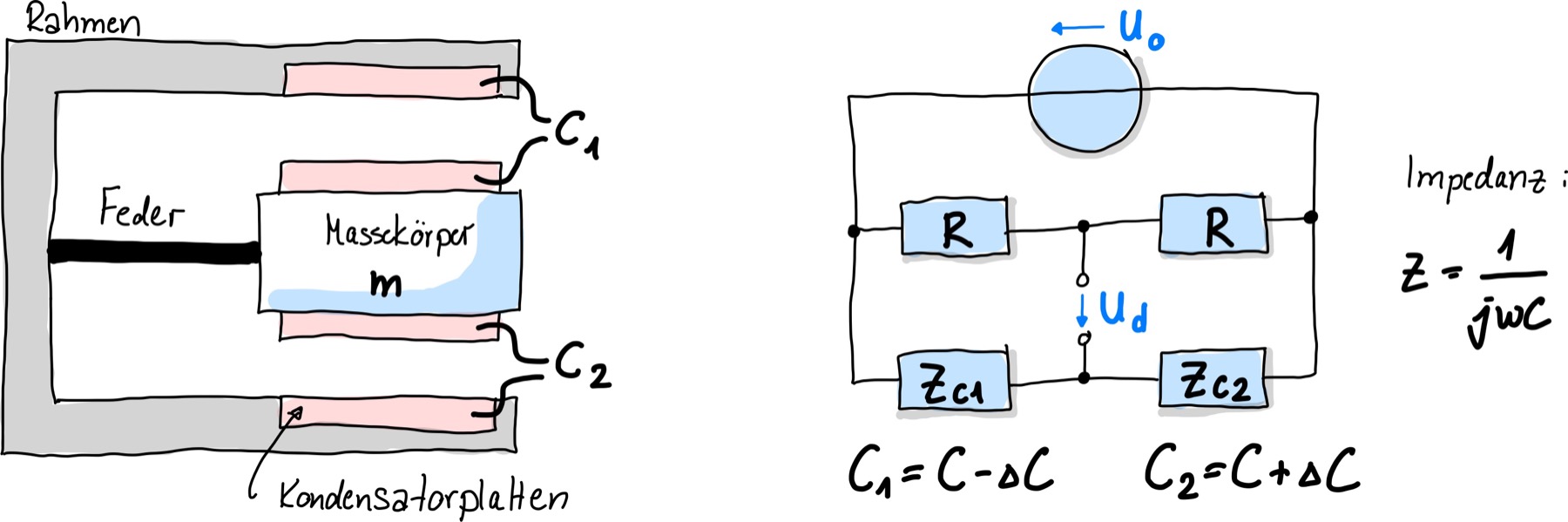
Abb. 127 Massekörper \(m\) ist an einer Feder aufgehangen. Mittels Kondensatoren werden Positions- und Lageänderungen gemessen. Genaueste Messungen erhält man mittels Brückenschaltung.

Der Massekörper ist nun gleichzeitig die Mittelelektrode eines Dreiplatten-Kondensators. Ändert der Massekörper seine Position um \(\Delta d\) aus der Ursprungslage \(d\), an ändern sich beide Kapazitäten symmetrisch aber gegensinnig um \(\Delta C\). Mittels der nebenstehenden Brückenschaltung wird diese Kapazitätsänderung ausgewertet.

Es wird eine Wechselspannung \(U_0\) angelegt, wodurch der Spannungsabfall \(U_1\) an einem der ohm’schen Widerstände \(R\) wiefolgt ist:

\[U_1 = \frac{U_0}{2}\]

Für die Masche mit den Kapazitäten (komplexen Widerständen \(Z = \frac{1}{j\omega C}\)) gilt für die Spannung \(U_2\), die an \(Z_2\) abfällt, entsprechend:

\[U_2 = U_0 \frac{Z_{C2}}{Z_{C1} + Z_{C2}}\]

Für die Diagonalspannung, die in der Messbrücke anfällt, folgt daraufhin:

\[U_d = U_1 - U_2 = \frac{U_0}{2} \frac{C_2 - C_1}{C_2 + C_1} = - \epsilon A \frac{U_0}{2} \frac{\Delta d}{d} \]

nachdem die Kapazitäten

\[C_1 = \frac{\epsilon A}{d - \Delta d}\]

und

\[C_2 = \frac{\epsilon A}{d + \Delta d}\]

eingesetzt wurden.

Mit diesem Differentialkondensator wird eine Spannung ausgegeben, die direkt proportional zur Auslenkung ist und damit proportional zur beschleunigenden Kraft. Möchte man die Kapazität des Kondensators erhöhen, vergrößert man die Flächen der Platten/Elektroden, indem man diese beispielsweise mäanderförmig anbringt. Typische Werte sind in der Größenordnung von pF für die Kapazitäten, wobei Änderungen im fF Bereich gemessen werden können. Aufgrund dieser extrem kleinen Werte wird die Auswerteelektronik direkt auf dem Sensorchip mitintegriert.

Kapazitive Beschleinigungssensoren können in etwa das 50-fache der Erdbeschleunigung messen, als ca. \(500\,\mathrm{m/s^2}\).

Piezoresistive Beschleunigungssensoren

In einem Feder-Masse-System wird die Auslenkung der Masse mittels piezoresistiver Komponenten erfasst. Werden diese Komponenten verformt, ändern sie ihren elektrischen Widerstand. Es handelt sich hierbei um Dehnungsmesstreifen, die aus Metall oder Halbleitermaterialien bestehen. Diese werden im Gegensatz zu anderen Beschleunigungssensoren meistens auf den Träger, den Biegebalken, bzw. die Feder angebracht, um ihre Dehnung zu messen. In Abhängigkeit der Dehnung oder Stauchung der Feder oder des Balkens ändert der Widerstand seinen Wert:

\[R = \rho \frac{l}{A}\]

wobei \(\rho\) der speizifische Widerstand ist, \(l\) die Länge des Leiters und \(A\) dessen Querschnittsfläche. Widerstandsänderungen können über den spezifischen Widerstand oder geometrische Änderungen der Leiterstruktur hervor gerufen werden, wie wir es in Kapitel Dehnungsmesstreifen behandelt haben. Diese Änderung ist im \(k\)-Faktor zusammengefasst:

\[\frac{\Delta R}{R} = \rho \frac{\Delta l}{l} = k \epsilon\]

Für Halbleiter-DMS dominiert die Änderung des spzifischen Widerstands, für Metalle die der geometrischen Längenänderung. Die Änderung der Querschnittsfläche ist meist vernachlässigbar.

Die Widerstandsänderung wird meist mittels eine Vollbrücke gemessen. Hierbei baut man 4 baugleiche DMSs ein, wobei zwei jeweils gestaucht bzw. gestreckt werden. Die Aussgangsspannung der Messbrücke ist dann proportional zur Widerstandsänderung und störende Einflüsse, wie z.B. Temepratur, werden kompensiert. Bei einer Vollbrücke gilt:

\[U_d = U_3 - U_1 = U_0 \left( \frac{R + \Delta R}{2R_0} - \frac{R - \Delta R}{2 R_0} \right) = U_0 \frac{\Delta R}{R} = U_0 k \epsilon \]

Piezoelektrische Beschleunigungssensoren

Es gibt Materialien die unter Krafteinwirkung eine elektrische Spannung erzeugen. Dies haben wir im Kapitel Piezoelektrische Sensoren kennengelernt. Mittels diesen Sensoren können natürlich auch Beschleunigungen gemessen werden.

Hall-Effekt Beschleunigungssensoren

Auch hierbei handelt es sich wieder um ein Feder-Masse-System, wobei die Masse nun ein Dauermagnet ist. Über dem System befindet sich ein Hall-Sensor und die Ausleselektronik für die Hall-Spannung. Unterhalb des Feder-Masse-Systems befindet sich eine Kupferplatte, die das System dämpft. Wird die Masse nun aufgrund einer externen Beschleunigungskraft aus ihrer Ruhelage ausgelenkt, verursacht sie eine Änderung der magnetischen Flussdichte \(B\) durch den Hall-Sensor. Dadurch verursacht sie eine Änderung der Hall-Spannung:

\[U_H = A_H \frac{I B }{d}\]

mit der Hall-Konstanten \(A_H\), der Stromstärke \(I\) und der Dicke der Probe, \(d\).