Widerstandsmessung#
Vielen Sensoren, die wir auch noch im Kapitel Sensoren kennenlernen werden, sind resistive Sensoren. Das heißt deren Widerstandverhalten ändert sich aufgrund der zu messenden Größe, wie z.B. Temperatur, Luftfeuchtigkeit oder Einstrahlung. Für die Messung eines ohmschen Widerstands nutzen wir folgende Formal
Genau wie bei der Leistungsmessung, müssen wir Strom und Spannung gleichzeitig messen. Hierbei entstehen Messfehler, da Messgeräte für Spannung und Strom Innenwiderstände besitzen, die die Widerstands- bzw. Leistungsmessung beeinflussen.
Stromrichtige Widerstandsmessung#
In Abb. 98 ist die stromrichtige Anschaltung zur Messung eines Widerstandswert gezeigt.
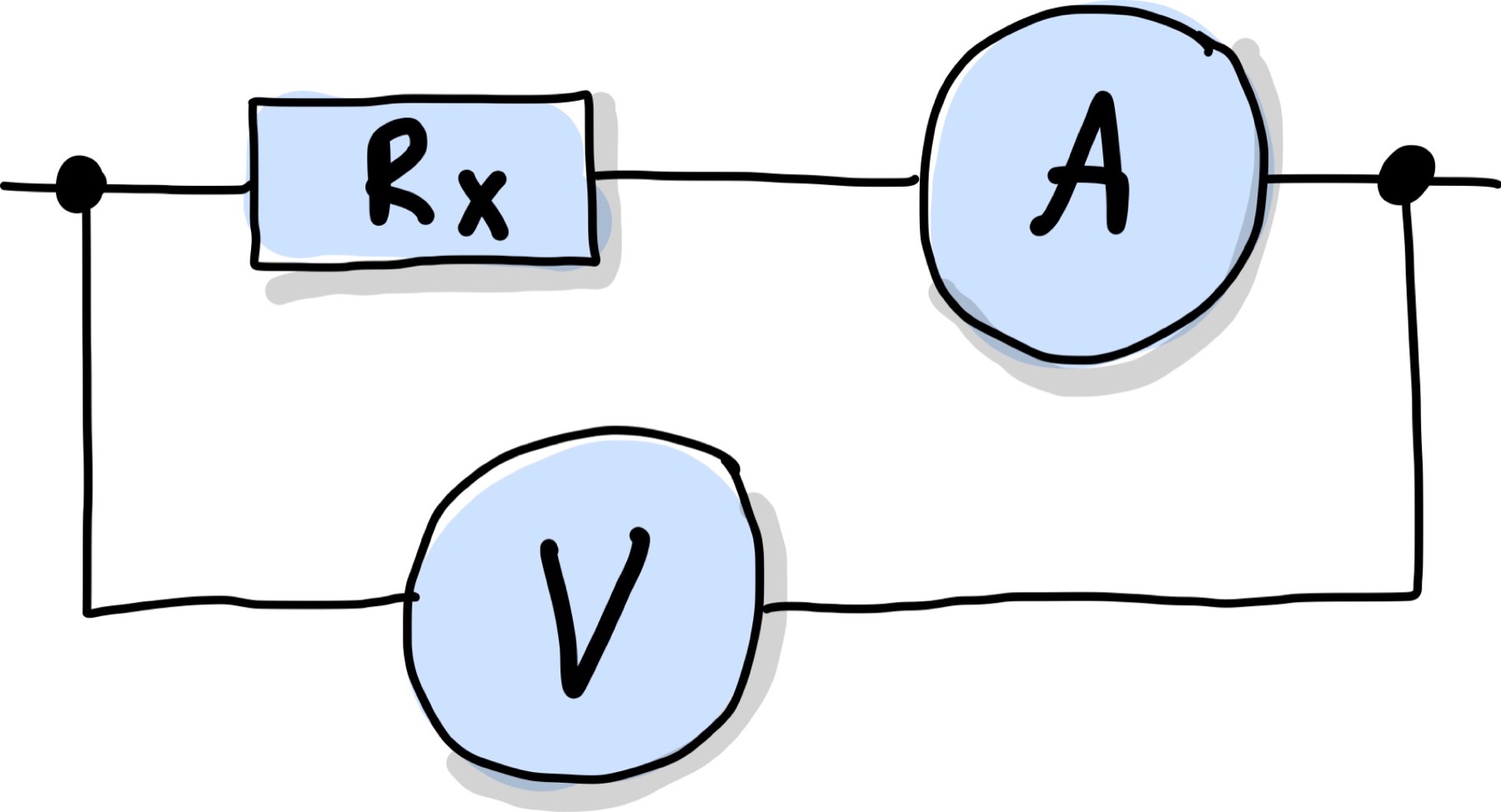
Abb. 98 Stromrichtige Schaltung zur Messung elektrischer Widerstände.#
Angenommen der Strommesseingang hat einen Innenwiderstand \(R_A\) und der Spannungsmesseingang \(R_V\), dann gilt für die Messung:
wobei \(R_x\) der gesuchte Messwert ist. Bei der stromrichtigen Anschaltung wird also der Innenwiderstand des Strommesseingangs \(R_A\) mitgemessen. Wie schon vorher bei der Leistungsmessung erläutert, handelt es sich auch hierbei um einen systematischen Fehler, der korrigiert werden sollte. Mittels Testmessung oder Herstellerangaben sollte \(R_A\) bekannt sein und vom Messergebnis subtrahiert werden.
Spannungsrichtige Widerstandsmessung#
In Abb. 99 ist die stromrichtige Anschaltung zur Messung eines Widerstandswert gezeigt.
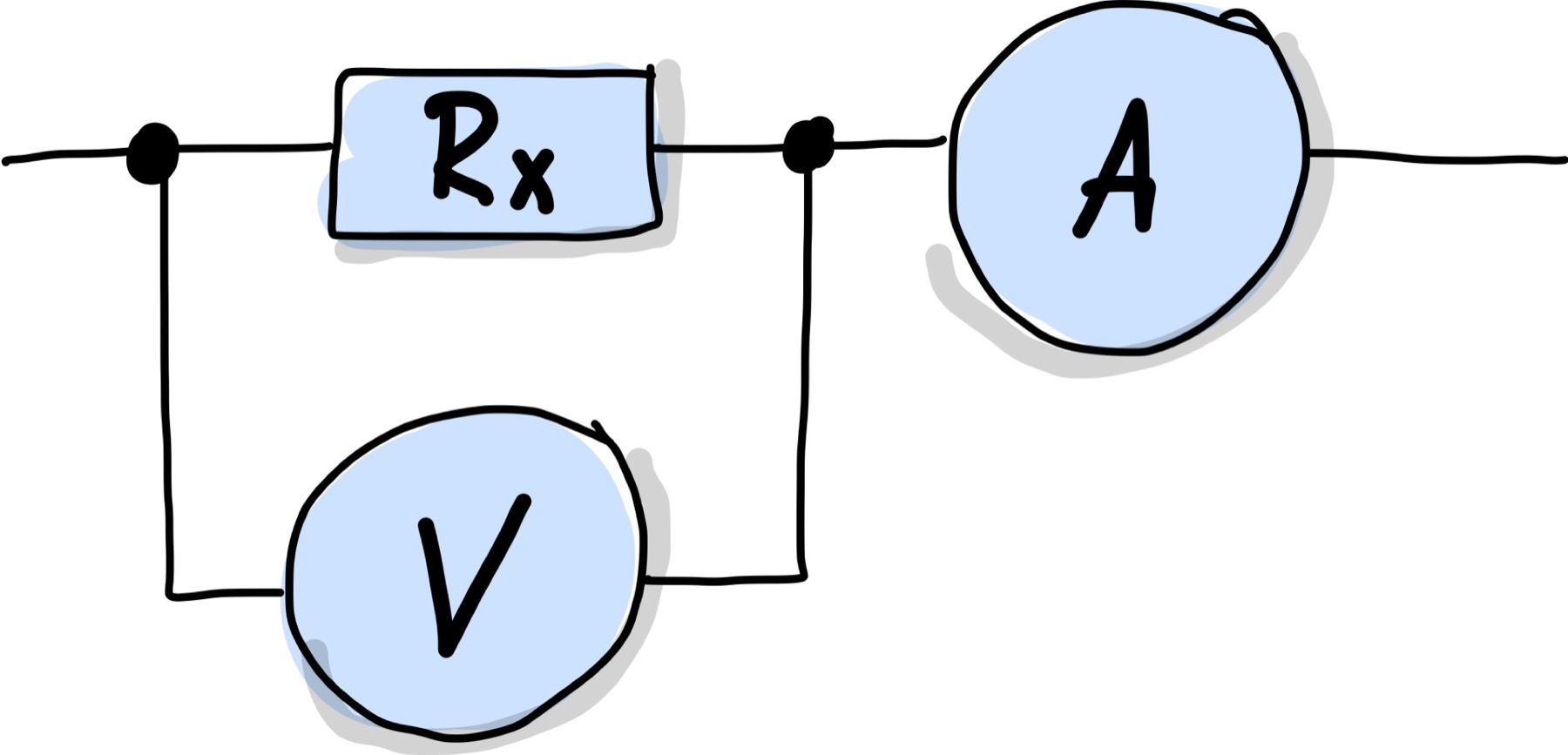
Abb. 99 Spannungsrichtige Schaltung zur Messung elektrischer Widerstände.#
Angenommen der Strommesseingang hat einen Innenwiderstand \(R_A\) und der Spannungsmesseingang \(R_V\), dann gilt für die Messung:
Jetzt wird ein zu kleiner Widerstandwert gemessen, der wieder korrigiert werden muss.
Bemerkung
Ist der gesuchte Widerstandswert \(R_x\) sehr viel kleiner als \(R_V\), so liefert die spannungsrichtige Anschaltung kleinere Messabweichungen. Dies ist bei den meisten resistiven Sensoren der Fall, aber nicht immer.
Widerstandsmessung mittels 2 Spannungsmessungen#
Für diese Methode benötigt man einen Referenzwiderstand \(R\), der in Reihe zu dem gesuchten Widerstand \(R_x\) geschaltet wird, wie in Abb. 100 dargestellt, und zwei Spannungsmesseingänge.
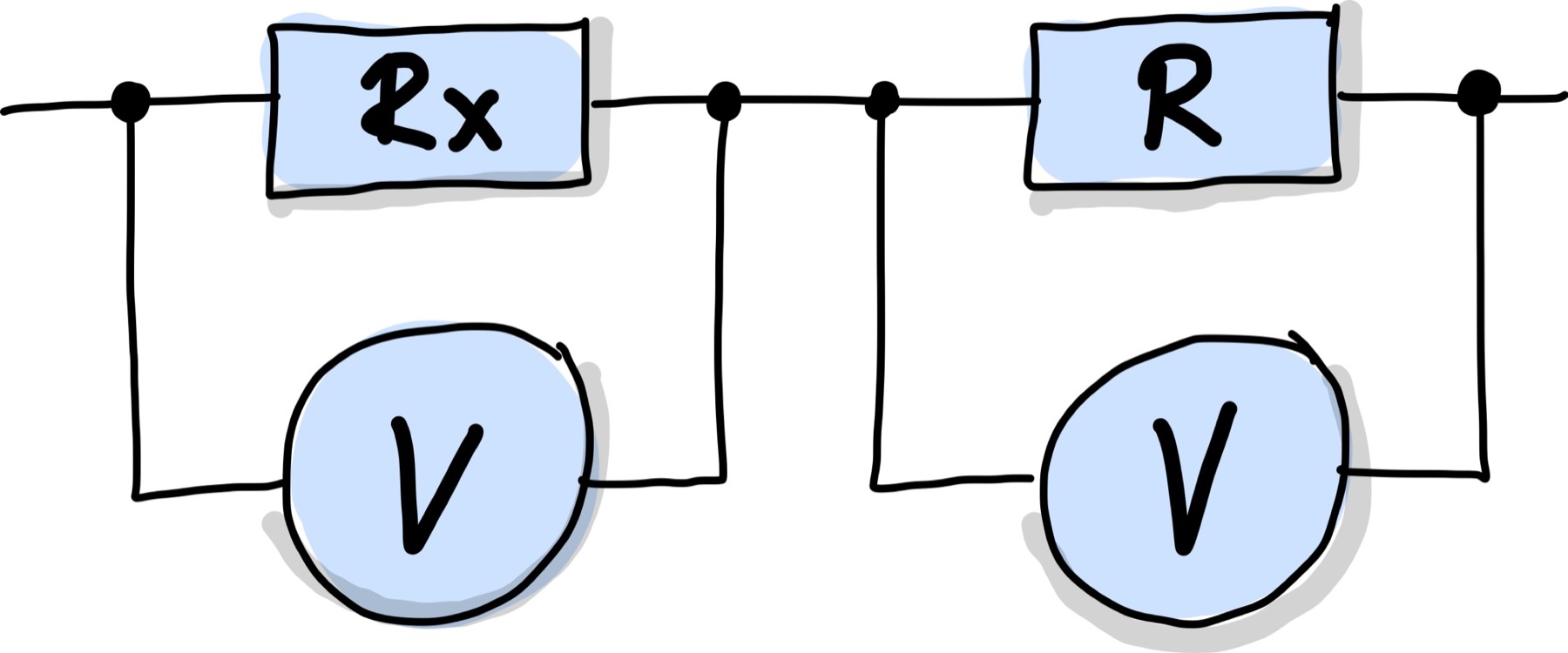
Abb. 100 Widerstandsmessung mittels 2 Spannungsmessungen (ohne Strommesseingang).#
Dieses Messprinzip hat den Vorteil, dass auf eine Strommessung verzichtet werden kann, die meistens ungenauer ist als eine Spannungsmessung, da der Strom durch Umformung erstmal in eine Spannung gewandelt werden muss. Zudem ist es schwierig kleine Innenwiderstände in Strommesseingängen zu realisieren.
Angenommen, beide Spannungsmesseingänge habe einen Innenwiderstand von \(R_V\), so kann die Spannung in jedem System bestimmt werden:
Für das Verhältnis der beiden Spannungen folgt:
wodurch man für den gesuchten Wert folgenden zusammenhang erhält:
Die beiden Widerstände \(R\) und \(R_x\) sollten hierbei ähnliche Werte haben. Je größer der Innenwiderstand \(R_V\) ist, desto besser gilt diese Näherungsformel. Ist \(R_V\) unbekannt, so liefert diese Methode deutlich kleinere Messabweichungen im Vergleich zu den Methoden mit Strommessungen. Ist \(R_V\) bekannt, so können auch hier systematische Abweichungen korrigiert werden.
Messabweichungen aufgrund von Kabelwiderständen#
Dieses Beispiel haben wir bereit im Kapitel Messunsicherheiten behandelt und wollen wir der Vollständigkeitshalber hier nur noch einmal aufführen.
Aufgrund der Innenwiderstände von Kabeln wird ein zu hoher Widerstandswert bemessen, der entsprechen korrigiert werden muss:
Hierbei ist \(\zeta\) der spezifische Widerstand, der für Kupfer \(0,0175\,\mathrm{\Omega mm^2/m}\) beträgt. \(l\) ist die Länge der Zuleitung und \(A\) der Querschnittfläche des Kabels.
Eine weitere Korrekturmöglichkeit ist hierbei die Vierleitertechnik, die eine Bestimmung des Kabelwiderstands nicht mehr benötigt. Das Kabel weist hier 4 Adern auf. An zwei Adern wird der Sensor/Widerstand mit einer Spannungsquelle verbunden, wodurch ein Stromfluss \(I\) generiert wird. An die anderen beiden Adern wird ein Spannungsmesseingang angeschlossen, um den Spannungsabfalll am Sensor/Widerstand zu messen. Aufgrund der hohen Innenwiderstands im Spannungsmesseingang fließt hier praktisch kein Strom, wodruch auch über die Kabellänge keine zusätzliche Spannung abfällt. Trotzdem wird Spannung direkt am Sensor/Widerstand gemessen und der Messwert \(R_x\) kann bestimmt werden:
Brückenschaltungen#
Um Messabweichungen bei der Widerstandsmessung zu vermeiden, kommen häufig Brückenschaltungen zum Einsatz. In Abb. 101 ist eine Wheatstone’sche Messbrücke gezeigt, die aus zwei parallelgeschalteten Spannungsteilern, \(R_1, R_2\) und \(R_3, R_4\) besteht. Die Verbindung zwischen dem oberen und unteren Spannungsteiler wird Brücke genannt. Eine Gleichspannungsquelle wird an diese Brücke angelegt und erzeugt die Brückenspannung, oder auch Diagonalspannung \(U_d\). Die Gesamtspannung teilt sich an den Widerständen auf. Ist das Verhältnis in beiden Spannungsteilern gleich, dann haben beide das gleiche Potential und an der Brücke fällt keine Spannung ab. Gibt es hingegen einen Potentialunterschied, so fließt ein Strom zwischen den beiden Spannungsteilern.
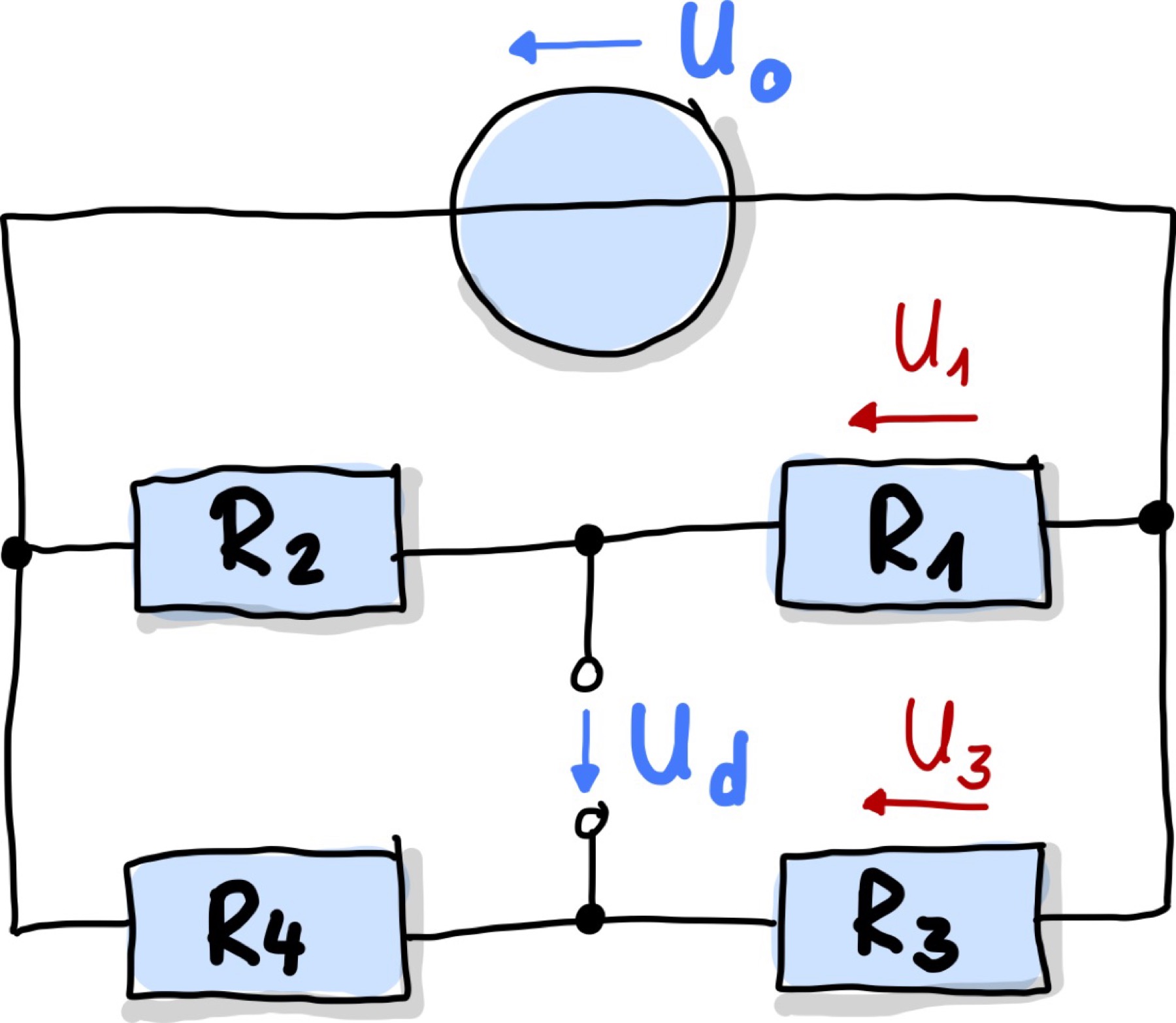
Abb. 101 Wheatstone’sche Widerstandsbrücke.#
Für die Einzelspannungen in den Spannungsteilern gilt:
Hieraus kann die Diagonalspannung berechnet werden, die zugleich auch die Kennlinie der Messbrücke ist:
Damit die Brücke im Gleichgewicht ist muss \(U_d = 0\) gelten:
Es folgt also:
und daraus die Abgleichbedingung:
In beiden Spannungsteilern muss also das gleiche Widerstandsverhältnis gelten. Sollte sich einer der Widerstandswerte ändern, so ist die Brücke nicht mehr im Gleichgewicht und es fließt ein Ausgleichsstrom.
Dies ist eine sehr empfindliche Anordnung, die auf kleinste Widerstandsänderungen reagiert und sofort einen messbaren Stromfluss bzw. Spannung generiert. Daher wird sie in der Messtechnik sehr häufig benutzt, in dem beispielsweise einer der Widerstände durch einen Sensor/Halbleiterbauelement ausgetauscht wird. Der Halbleiter reagiert auf Temperatur, Luftfeuchte, Licht oder ähnliches und ein Stromfluss, oder Potentialdifferenz, ist sofort messbar.
Limitierungen bestehen in der Genauigkeit der Spannungsmessung und es kann unter Umständen aufwendig sein die Widerstandswerte anzupassen und zu wechseln.
Viertelbrücke / Ausschlagsbrücke#
Die einfachste Brückenschaltung ist die Viertelbrücke. Nur ein Vertiel aller vier Widerstände ist hierbei veränderlich, nämlich genau einer. Hier wird dann z.B. ein Sensor eingebaut, dessen Widerstand \(R_x\) sich in Abhängigkeit von einer Messgröße \(x\) ändert. Die anderen drei Widerstände haben feste, gleiche Widerstandswerte \(R\). Der genaue Wert von \(R\) muss richtig bestimmt werden. Die Schaltung ist in Abb. 102 dargestellt.
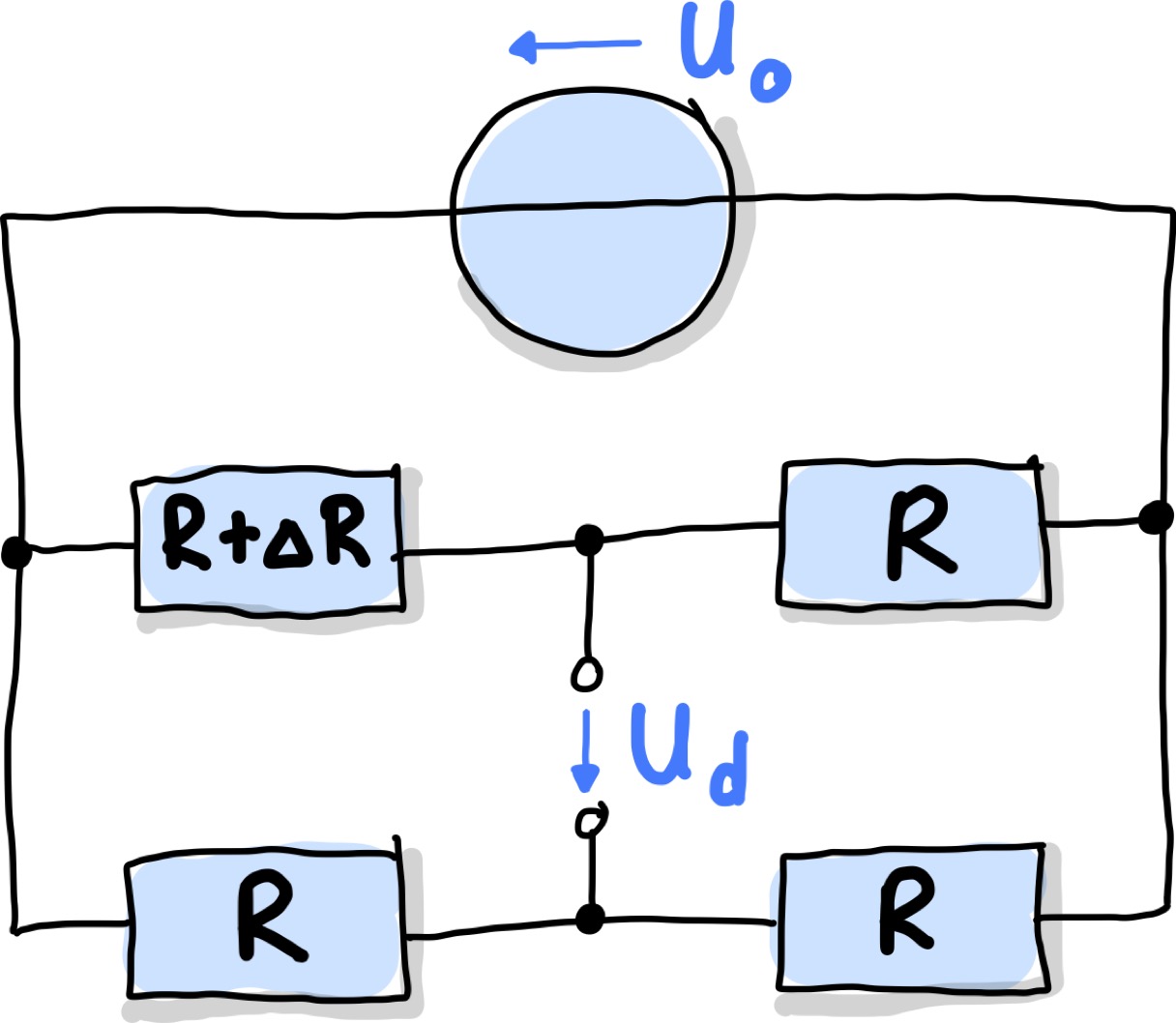
Abb. 102 Viertelbrücke oder auch Ausschlagsbrücke genannt.#
Angenommen, der zu messende Widerstandswert \(R_x = R(x)\) setzt sich aus einem Grundwert \(R\) und einer kleinen Widerstandsänderung \(\Delta R(x)\) zusammen. Die Widerstandsänderung \(\Delta R(x)\) ändert sich in Abhängigkeit von der zu messenden Messgröße \(x\). Wenn keine Messgröße angelegt ist, also \(x=0\), nimmt \(R(x)\) den Grundwert \(R\) an. Es gilt:
Für die Brücke selber können wir wieder die Kennlinie auffschreiben. Hierfür benutzen wir die obige Formel und setzen die Widerstandswerte \(R_2 = R(x) = R + \Delta R(x)\) und \(R_1 = R_3 = R_4 = R\) ein. Die drei Brückenwiderstände müssen dabei immer dem Grundwert \(R\) des zu messen Widerstands entsprechen, \(R(x)\)! Dadurch erhalten wir:
beziehungsweise nach Umstellen:
Der Zusammenhang ist im folgenden Plot dargestellt:
Show code cell source
#Benötigte Libraries:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
ratio_R = np.linspace(-1,1,100) # Zeitwerte der Sinusfunktion in sec
ratio_U = ratio_R / (2 * (2 + ratio_R))
fig = plt.figure(figsize=(4,3))
plt.axvline(x = 0., ls = '--', lw = 1, color = 'k')
plt.axhline(y = 0., ls = '--', lw = 1, color = 'k')
plt.plot(ratio_R,ratio_U, 'tab:blue')
plt.xlabel(r'$\Delta R / R$')
plt.ylabel(r'$U/U_0$')
plt.show()
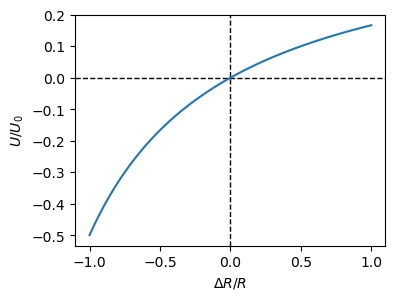
Ist kein Messeffekt vorhanden, d.h. \(\Delta R = 0\), dann ist \(U_d = 0\). Dadurch kann die Brücke gut auf den Nullpunkt kalibriert werden. Außerdem sieht man, dass für eine postive Änderung von \(\Delta R\) sich auch die Spannung in positive Richtung ändert. Das Vorzeichen kann man umkehren, indem man beispielsweise statt des Widerstands oben recht den unten links durch \(R(x)\) ersetzt oder die Versorgungsspannung \(U_0\), oder Brückenspannung \(U_d\), umpolt. Die Kennlinie ist allerdings nicht linear. Solange die Änderungen in klein sind, \(\lvert \Delta R \rvert << R\), ist dies nicht schlimm. Auf kleinen Skalen verhält sie sich fast linear, wie z.B. Nahe des Nullpunkts und es gilt:
Gilt die Bedingung \(\lvert \Delta R \rvert << R\) nicht mehr, da die Dynamiken der Messgröße zu groß sind, müssen Korrekturstufen nachgeschaltet werden.
Halbbrücke#
Stehen einem zwei baugleiche zu messende Widerstände/Sensoren zur Verfügung, die die Messgröße \(x\) in jeweils entgegensetzter Richtung aussteuert, können diese mit einer Halbbrücken-Schaltung wie in Abb. 103 dargestellt ausgelesen werden.
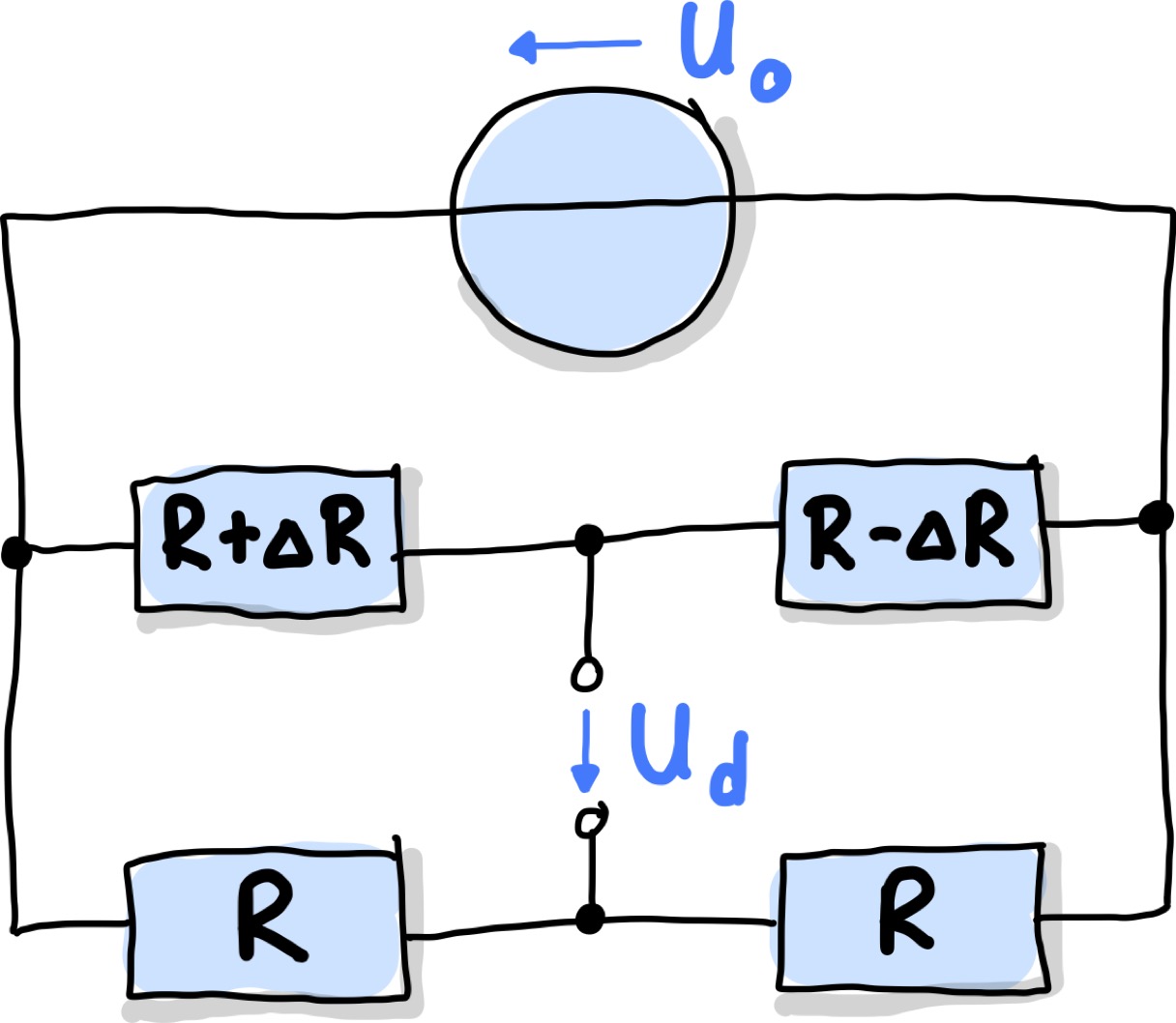
Abb. 103 Halbbrücke mit zwei baugleichen Sensoren, die entgegengesetzt ausgesteuert werden: \(R(x) = R \pm \Delta R(x)\)#
Betragsmäßig führt \(x\) zu der gleichen Widerstandsänderung, jedoch mit entgegengesetztem Vorzeichen. Das heißt als Ausgangsspannung, bzw. Kennlinie, erhalten wir nun
Aufgabe
Leite die Gleichung für die Kennlinie einer Halbbrücke her.
Der Zusammenhang ist im folgenden Plot dargestellt:
Show code cell source
#Benötigte Libraries:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
ratio_R = np.linspace(-1,1,100) # Zeitwerte der Sinusfunktion in sec
ratio_U = ratio_R / (2)
fig = plt.figure(figsize=(4,3))
plt.axvline(x = 0., ls = '--', lw = 1, color = 'k')
plt.axhline(y = 0., ls = '--', lw = 1, color = 'k')
plt.plot(ratio_R,ratio_U, 'tab:blue')
plt.xlabel(r'$\Delta R / R$')
plt.ylabel(r'$U/U_0$')
plt.show()
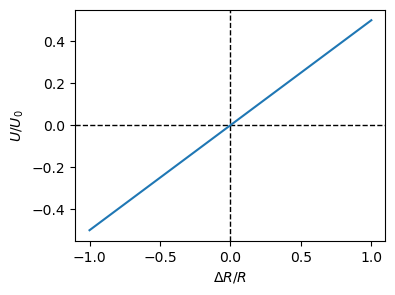
Dadurch erhält man drei Vorteile:
die Kennlinie ist über den kompletten Bereich linear
die Ausgangsspannung ist doppelt so groß wie bei der Viertelbrücke und liefert somit bessere Signalqualität
Störgrößen, wie \(\Delta R(T)\) in Abb. 104 dargestellt, die auf die zu messenden Widerstände/Sensoren \(R(x)\) wirken haben keinen großen Einfluss auf die Kennlinie, solange es sich um kleine Widerstandsänderungen (\(<< R\)) handelt
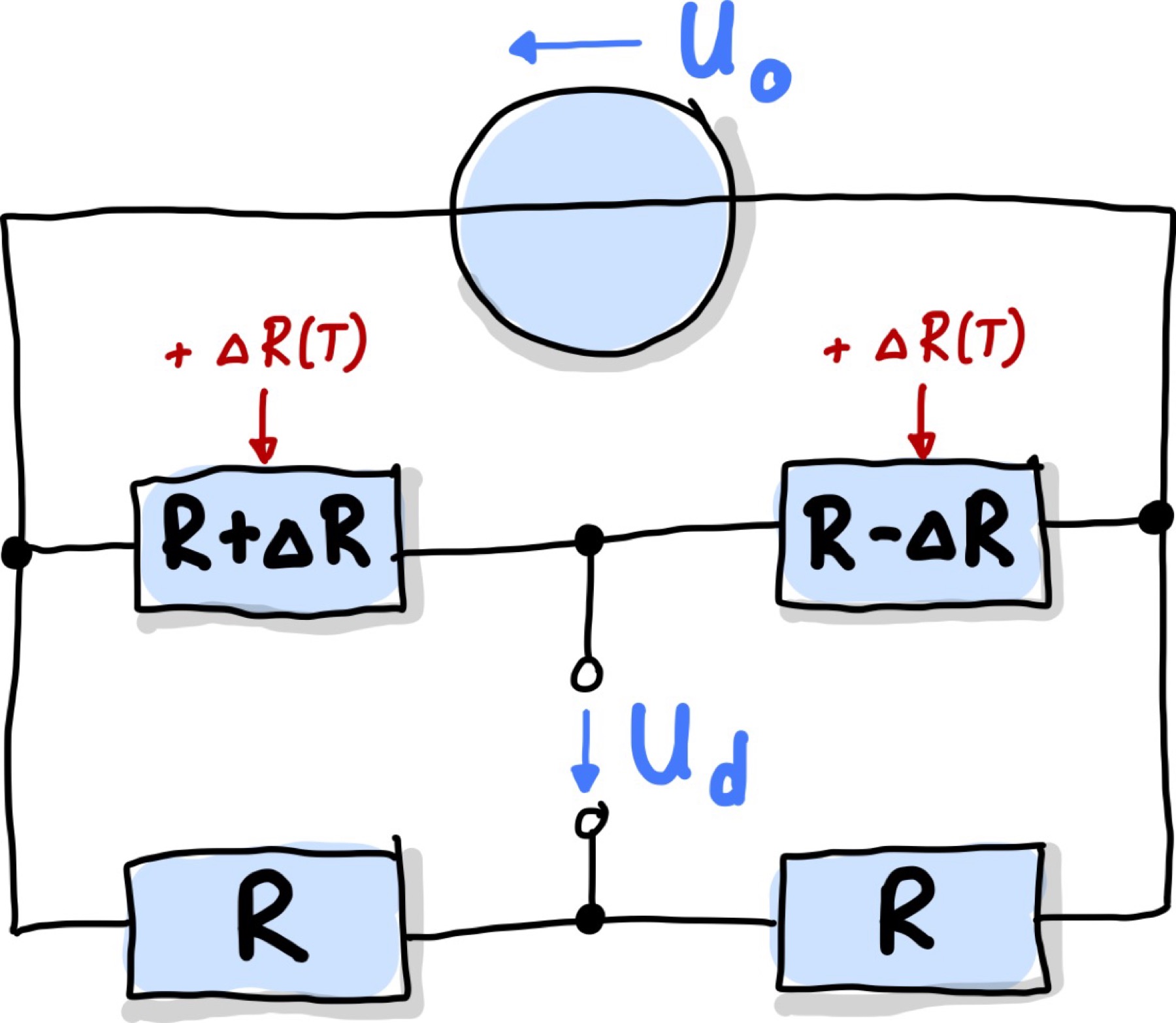
Abb. 104 Halbbrücke mit zwei baugleichen Sensoren, die aufgrund externe Einflüsse (z.B. Temperatur) ihren Widerstand gleichgesinnt ändern: \(R(x) = R \pm \Delta R(x) + \Delta R(t)\)#
Aufgabe
Nimm an, dass eine Temperaturänderung in gleicher Weise auf die Widerstandswerte/Sensoren mit \(\Delta R(T)\) einwirkt:
Was folgt dann für die Aussgangsspannung \(U(x)\), insbesondere für kleine Temperatureinflüsse \(\lvert \Delta R(T) \rvert << R\)? Bleibt die Kennlinie linear?
Aufgrund der Störgrößenunterdrückung sollte man eine Halbbrücke immer der Viertelbrücke vorziehen, insofern eine entgegengesetzt Aussteuerung der Widerstände/Sensoren möglich ist. Häufig werden Dehnungsmessstreifen in einer solchen Halbbrücke betrieben.
Vollbrücke#
Bringt man nun an jeden der 4 Positionen einen Sensor an, so nennt man dies die Vollbrücke, welche in Abb. 105 dargestellt ist.
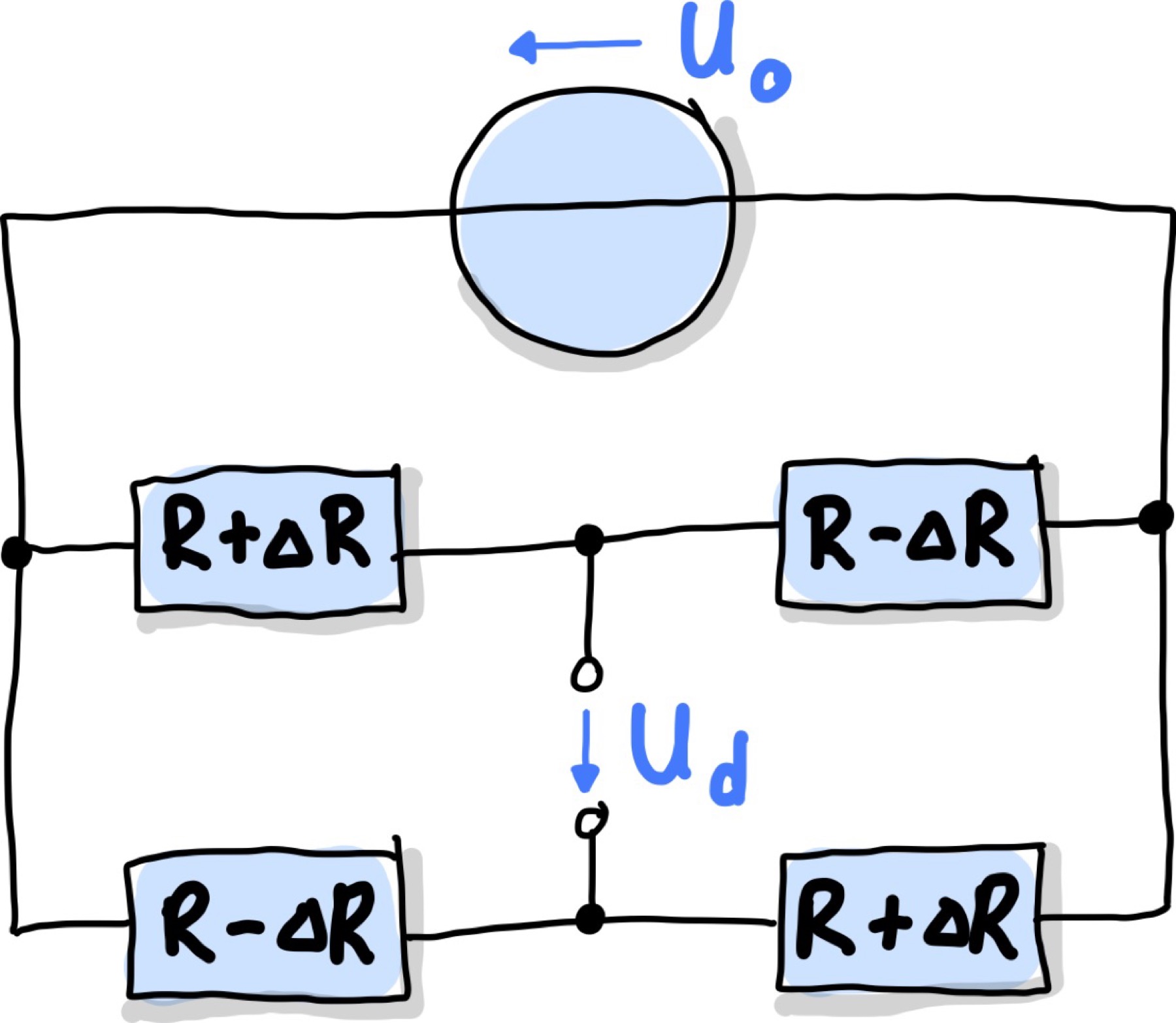
Abb. 105 Vollbrücke mit vier baugleichen Sensoren.#
Für die Kennlinie gilt
Aufgabe
Leite die Gleichung für die Kennlinie einer Vollbrücke her.
Der Zusammenhang ist im folgenden Plot dargestellt:
Show code cell source
#Benötigte Libraries:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
ratio_R = np.linspace(-1,1,100) # Zeitwerte der Sinusfunktion in sec
ratio_U = ratio_R
fig = plt.figure(figsize=(4,3))
plt.axvline(x = 0., ls = '--', lw = 1, color = 'k')
plt.axhline(y = 0., ls = '--', lw = 1, color = 'k')
plt.plot(ratio_R,ratio_U, 'tab:blue')
plt.xlabel(r'$\Delta R / R$')
plt.ylabel(r'$U/U_0$')
plt.show()
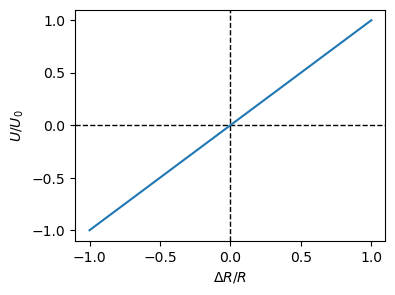
Die Ausgangsspannung ist gegenüber der Halbbrücke noch ein weiteres mal verdoppelt.
Mit einer externen Störgröße, \(\Delta R(T)\) und dadurch \(R(x) = R \pm \Delta R(x) + \Delta R(T)\) ergibt sich folgender Zusammenhang:
wobei im letzten Schritt wieder angenommen wurdem dass es sich um kleine Störeffekte handelt, \(\Delta R(T) << R\). Störgrößen werden also auch in einer Vollbrücke kompensiert und die Kennlinie bleibt linear.
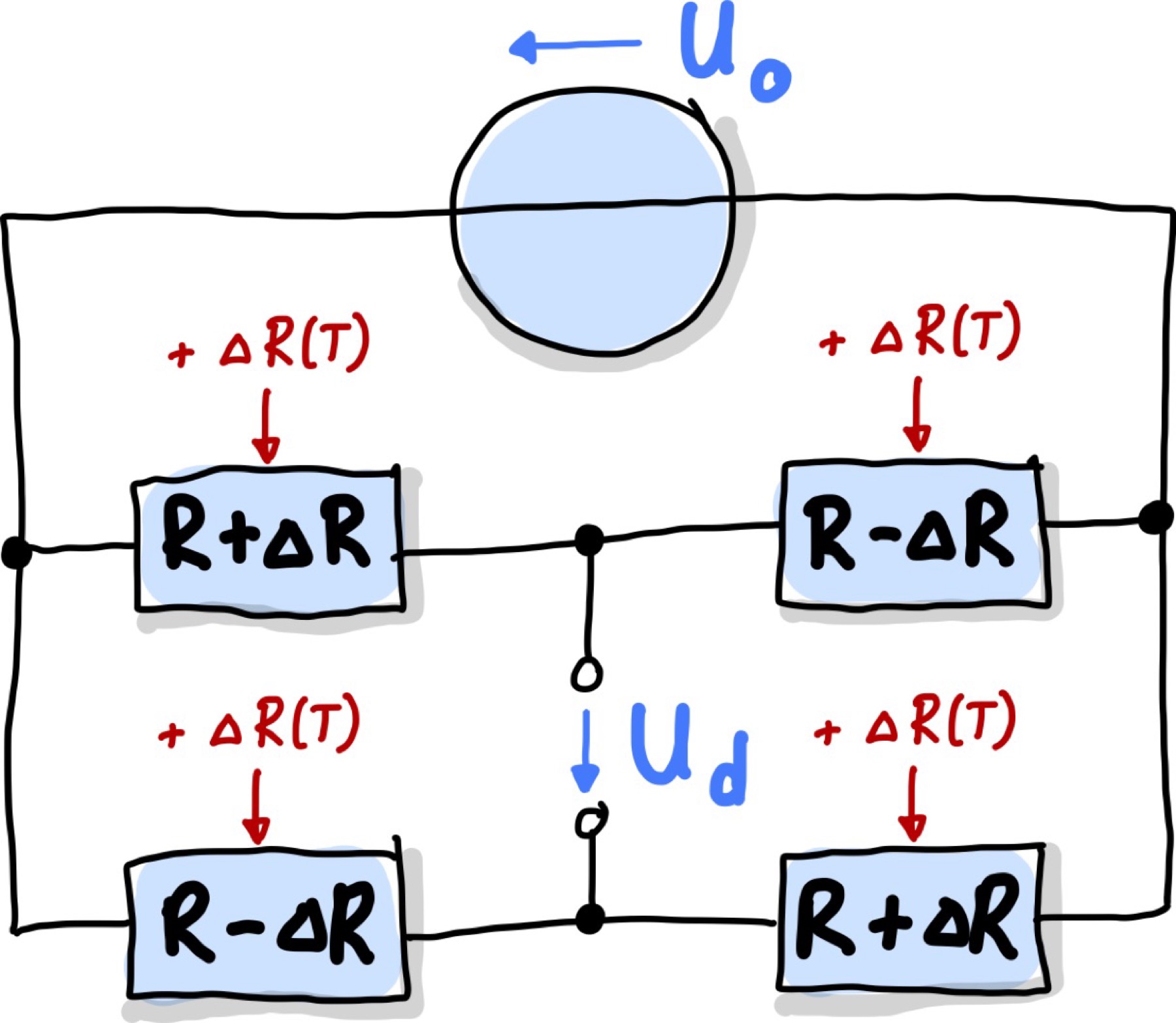
Abb. 106 Halbbrücke mit zwei baugleichen Sensoren, die aufgrund externe Einflüsse (z.B. Temperatur) ihren Widerstand gleichgesinnt ändern: \(R(x) = R \pm \Delta R(x) + \Delta R(t)\)#


