Kapazitive und Induktive Sensoren

Möchte man kleiner Abstände, so in der Größenordnung von etwa einem Mikrometer bishin zu mehreren Millimetern messen kann man dies sehr gut kapazitiven oder induktiven Sensoren ermöglichen.

Kapazitive Sensoren

In Abb. 120 ist ein Plattenkondensator dargestellt, der seine Kapazität in Abhängigkeit von verschiedenen Parametern ändert.

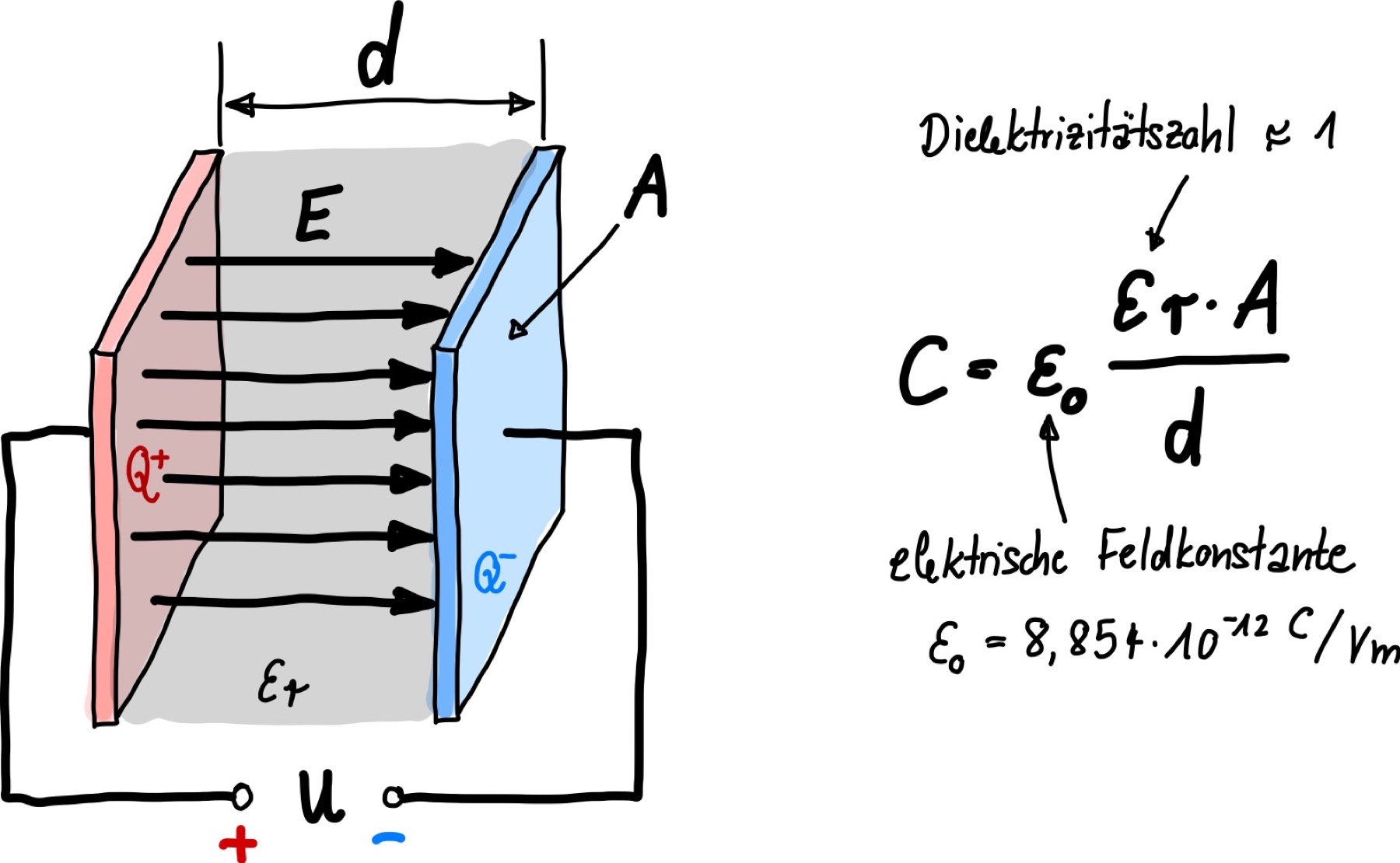
Abb. 120 Kapazität eines Kondensators.

\[C = \epsilon_0 \cdot\frac{\epsilon_r A }{d}\]

• elektrische Feldkonstante, ist eine Konstante, und beträgt \(\epsilon_0 = 8,854\cdot 10^{-12}\,\mathrm{C/Vm}\)

• die Dielektrizitätszahl \(\epsilon_r\) des Elektrikums ist für Luft =1, für ein andere Medium, was sich zwischen den Platten eines Kondensators befindet, weicht es von Null ab. Dadurch kann man z.B. Füllhöhen von nichtleitenden Flüssigkeiten bestimmen.

• der Abstand \(d\) der beiden Kondensatorplatten. Hierüber sind Längenmessungen entlang der Kondensatorachse möglich.

• die Fläche \(A\) der sich überlappenden Kondensatorplatten. Verschiebt sich eine Platte relativ der anderen so verringert sich die effektive Fläche des Plattenkondensator. Dadurch können auch Bewegungen senkrecht zur Kondensatorachse gemessen werden.

Diese Parameter können durch physikalische Messgrößen verändert werden. Mittels Messung der Kapazität (also der Impedanz = komplexer Widerstand) kann somit auf eine physikalische Messgröße zurückgeschlossen werden.

Induktive Sensoren

Ähnliche wie bei kapazitiven Sensoren betrachten wir bei induktiven Sensoren zunächst die grundlegende Formel, wie sich eine Induktivität einer Spule berechnen lässt:

\[L = \frac{N^2}{R_M}\]

• \(N\) ist die Anzahl der Windungen der Spule

• \(R_M\) ist der magnetische Widerstands der Umgebung, den die magnetischen Feldlinien außerhalb der Spule einnehmen. Der Widerstand für einen magnetischen Kern ist z.B.

\[R_{M,\mathrm{Kern}} = \frac{s}{\mu_0 \mu_r A}\]

• \(s\) ist die Länge des Kerns (z.B. des Eisenkerns)

• \(A\) ist die Querschnittsfläche des Kerns

• \(\mu_0 = 1,257 \cdot 10^{-6}\,\mathrm{Vs/Am}\) ist die magnetische Feldkonstante

• \(\mu_r\) ist die Permeabilitätszahl (hängt vom Kernmaterial ab), bei Eisen beträgt sie etwa 10.000 und der Widerstand ist vernachlässigbar. Für Luft ist sie etwa 1.

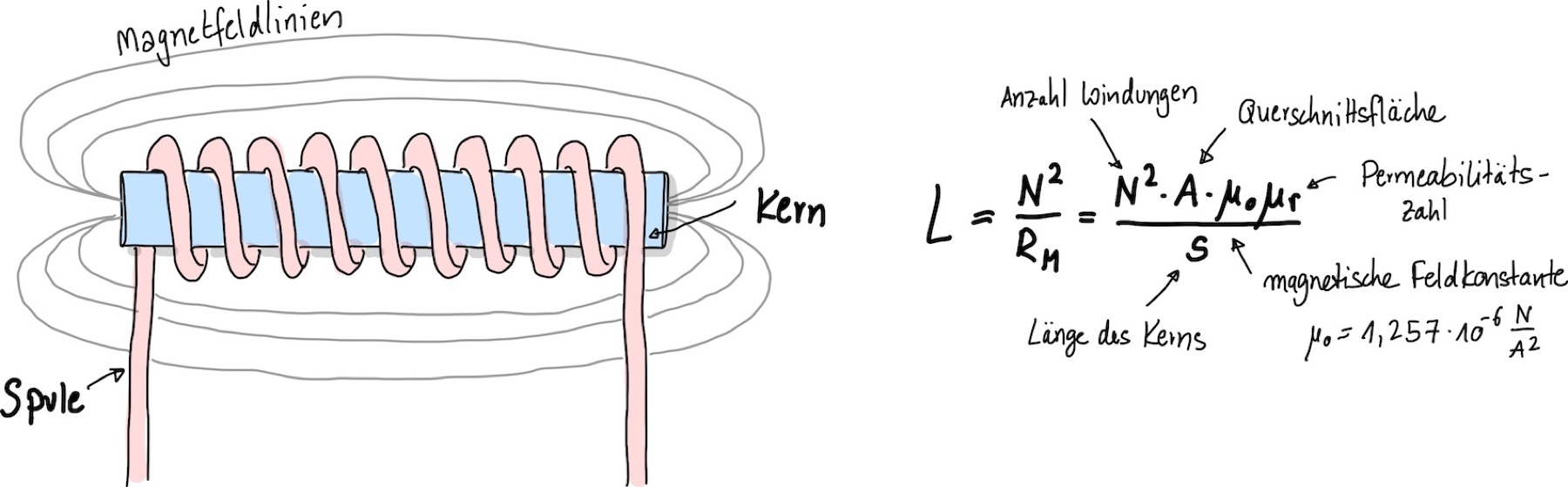
Abb. 121 Induktivität einer Spule.

Der magnetische Widerstand kann für bestimmte Umgebungen abgeschätzt werden:

• für einen Eisenkern beträgt \(\mu_r = 10.000\) und somit gilt

\[R_{M,\mathrm{Eisen}} \approx 0\]

• für Luft ist \(\mu_r = 1\) und somit gilt:

\[R_{M,\mathrm{Luft}} = \frac{s}{\mu_0 A}\]

• für Luft außerhalb der Spule wird die Fläche unendlich groß, \(A \rightarrow \infty\) und es gilt wieder

\[R_{M,\textrm{Luft außerhalb}} \approx 0\]

Nur innerhalb der Spule weißt die Luft eine begrenzte Fläche auf und hat somit einen von Null verschiedenen magnetischen Widerstand, wodurch die Induktivität berechnet werden kann. Für eine reine Luftspule gilt also:

\[L = \frac{N^2}{R_M} = \frac{N^2}{\frac{s}{\mu_0 A}}\]

Abstandssensoren

Wie man einen Kondensator als Abstandssensor benutzen kann, ist in Abb. 122 dargestellt:

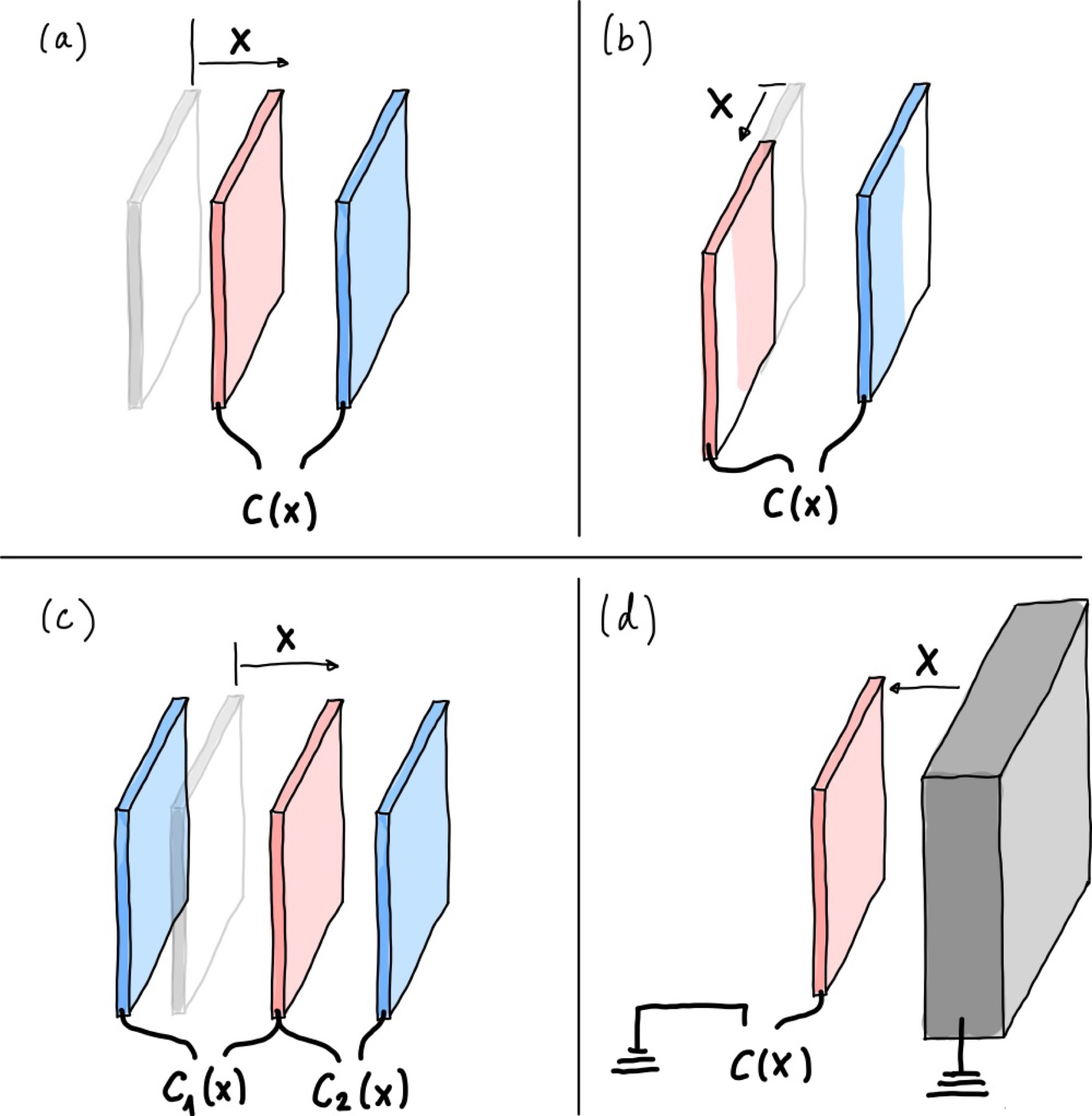
Abb. 122 Kondensator als Abstandssensor.

• in (a) ändert sich der Abstand \(d\) der Platten und ändert somit die Kapazität antiproportional

• in (b) ändert sich die effekte Plattenfläche und ändert somit linear die Kapatität

• in © ist ein Differentialkondenstor dargestellt. Zwei Kapazitäten werden gemessen und verhalten sich genau entgegengesetzt, wenn sich die mittlere Kondensatorplatte bewegt. Die gegensinnigen Kapazitäten können mittels Halbbrücke ausgelesen werden. Bei nicht zu großen Bewegungen verhält ist die Kennlinie linear.

• in (d) wird einfach ein Teil einer Maschine oder Objektes als zweite Kondensatorplatte benutzt. Deren Position bzw. Bewegung kann somit berührungslose gemessen werden. Allerdings muss man hierbei darauf achten, dass die Maschine geerdet ist und somit ein definiertes Potential hat, gegen welches am Ende die Kapazität gemessen werden.

Wie man eine Spule als Abstandssensor benutzen kann, ist in Abb. 123 dargestellt:

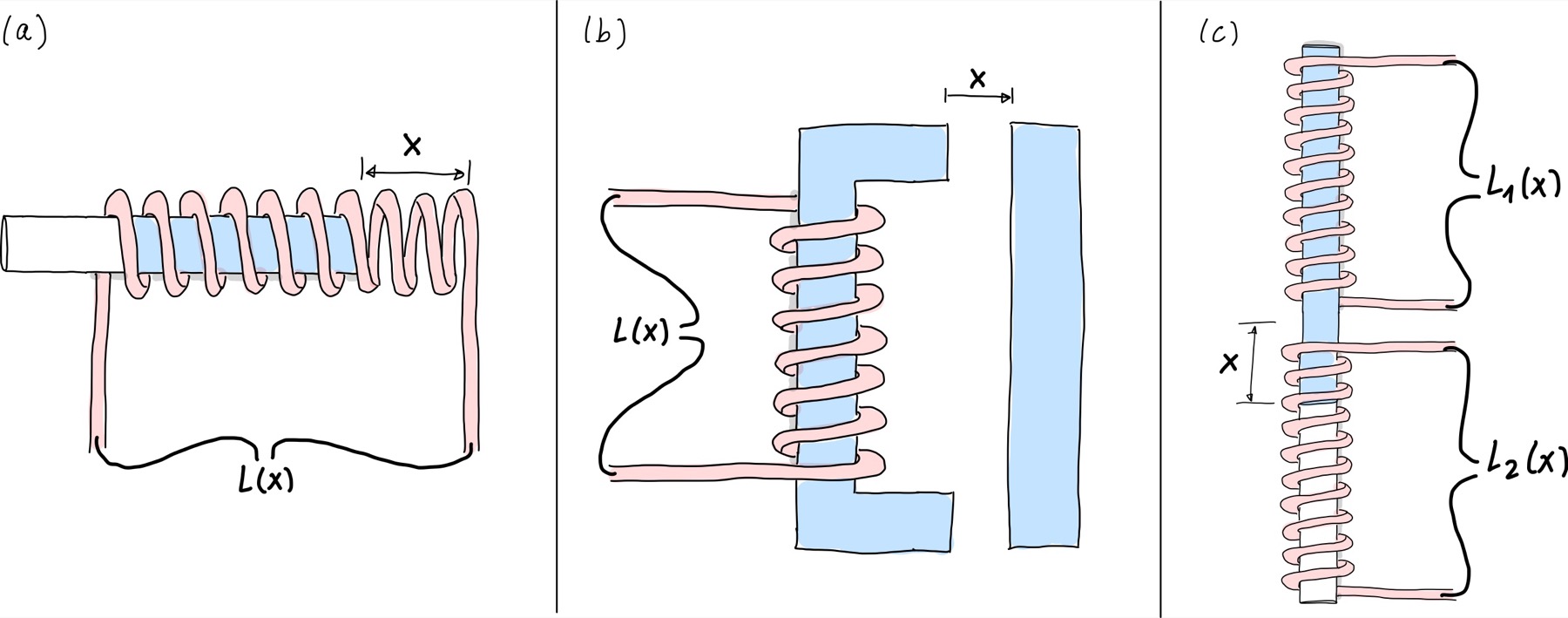
Abb. 123 Spule als Abstandssensor.

• in (a) ist der Magnetkern im Inneren der Spule beweglich. In dem Teil der Spule wo sich der Kern befindet besteht somit ein großer magnetische Widerstand. In Abhängigkeit von der Position des Magnetkerns ändert sich der Widerstand, welcher die Induktivität beeinflusst. Über die Messung der Induktivität kann also die Strecke \(x\) gemessen werden, um die sich die Magnetkernposition verändert hat. Diese Anordnung wird Tauchanker genannt.

• in (b) die Magnetfeldlinien durch einen Magneten weiter geführt. Hierbei handelt es sich um einen U-förmigen Magnetkern und einen Magnetstab. Zwischen U-förmigen Magnetkern und Magnetstab befindet sich ein Luftspalt. In diesem Luftspalt existiert ein magnetischer Widerstand, der sich mit dem Abstand \(x\) zwischen den beiden Magneten ändert und zu einer Induktivitätsänderung führt.

• in © ist ein Tauchanker in einer Differentialanordnung dargestellt. Es werden zwei Teilinduktivitäten gemessen, die sich in Abhängigkeit der Position des Magnetkerns ändern. Mit einer Halbbrücke können die Induktivitäten bestimmten werden.

Eine weitere Möglichkeit Abstände mittels Induktivitäten zu messen ist der Wirbelstromsensor wie in Abb. 124 dargestellt. Eine Spule erzeugt ein Magnetfeld. Die magnetische Flussdichte \(B\), die daraus resultiert, wirkt sich auf die zu messende Oberfläche aus. Ist diese Oberfläche elektrisch leitfähig, also aus Metall, so wird entsprechend der Lenz’schen Regel durch die magnetische Flussdichte \(B\) ein Wirbelstrom \(I\) induziert, der im Kreis auf der Oberfläche fließt. Der Wirbelstrom \(I\) verursacht wiederum ein Magnetfeld \(B_2\) was dem ursprünglichen Magnetfeld \(B\) entgegen gerichtet ist. Die beiden B-Felder heben sich dadurch teilweise auf wodurch die Induktivität abnimmt.

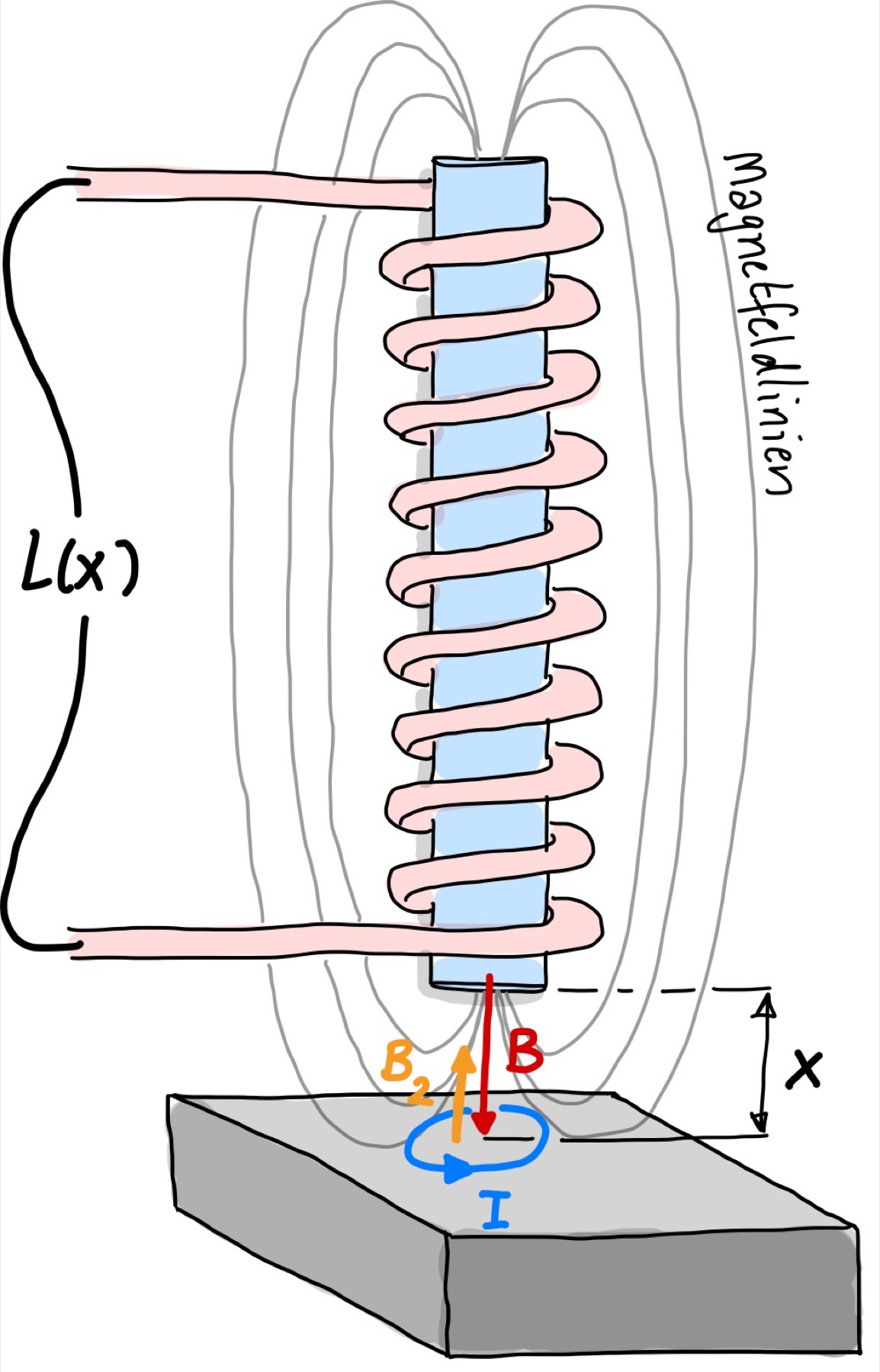
Abb. 124 Spule als Wirbelstromsensor zur Abstandsmessung.

Füllstandssensoren

Wie man einen Kondensator als Füllstandssensor benutzen kann, ist in Abb. 125 dargestellt:

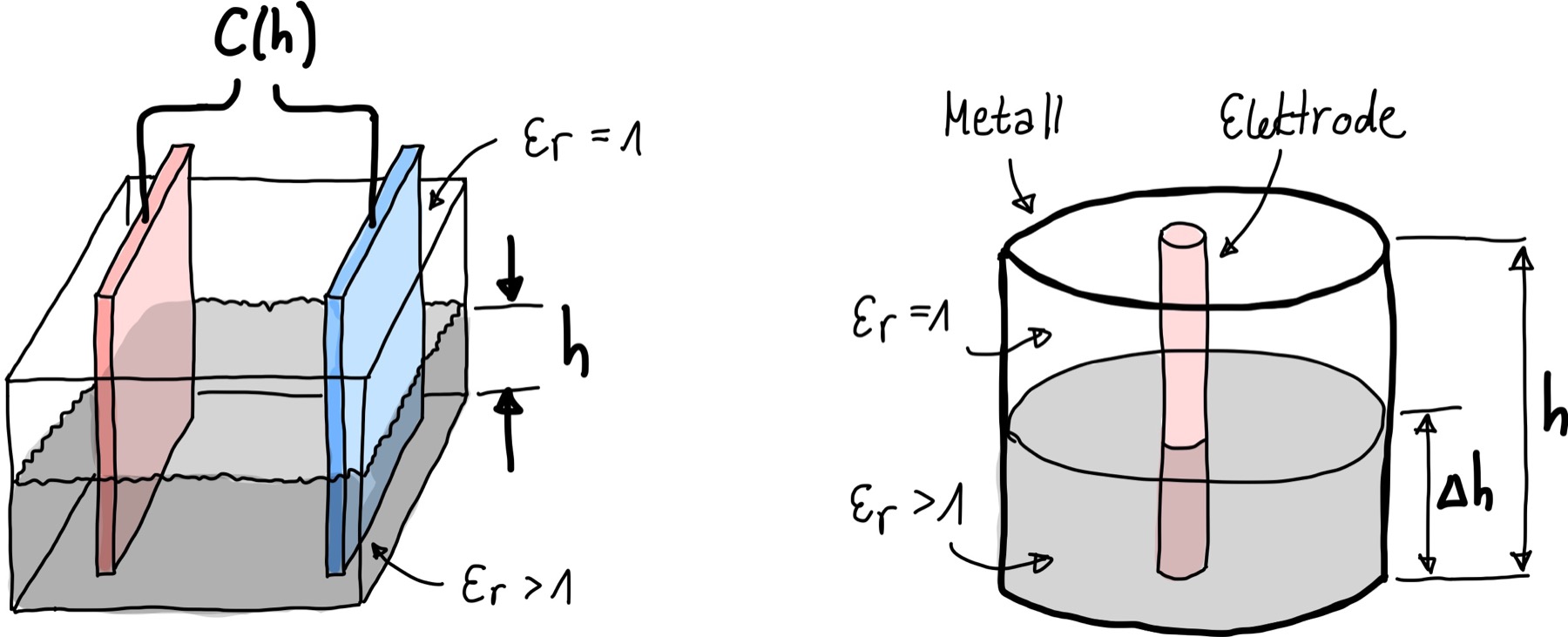
Abb. 125 Kondensator als Füllstandssensor benutzen.