Infos zum Praktikum#
Vor Beginn deines ersten Praktikumsversuchs ist es wichtig, folgendes Grundwissen zu beachten:
Einheiten: Welche Maßeinheiten gibt es? Was sind SI-Einheiten? Welche Präfixe sind gebräuchlich?
Messunsicherheiten: Welche Arten von Unsicherheiten gibt es? Welche statistischen Methoden stehen zur Verfügung, um Messreihen auszuwerten? Wie werden Messunsicherheiten angegeben (Messwert und Fehlerbalken)?
Fehlerfortpflanzung: Wie wird die Fehlerfortpflanzung durchgeführt? Welche Besonderheiten sind bei systematischen, zufälligen und korrelierten Unsicherheiten zu beachten?
Kurvenanpassung: Wie werden Messdaten sinnvoll visualisiert? Wie kann man Zusammenhänge in den Daten darstellen?
Grundidee: Daten sammeln#
Die Messtechnik dient dazu, physikalische Größen quantitativ zu beobachten und ist daher ein wesentlicher Bestandteil der Physik. Eine quantitative Beschreibung erfordert immer einen Zahlenwert, \(x\), und eine Maßeinheit, \(E\). Um einen möglichst genauen experimentellen Wert zu erzielen, wird ein erheblicher Teil der Experimentierzeit für die Vorbereitung und Planung des Experiments sowie für die Datenauswertung aufgewendet. Dabei werden auch Daten aufgenommen und visualisiert, um Ergebnisse zu überprüfen und gegebenenfalls Messungen zu wiederholen. Es ist wichtig zu beachten, dass Messungen immer zufälligen Schwankungen unterliegen, was bedeutet, dass das Messergebnis immer variieren wird. Eine Messung wird niemals den wahren Wert liefern können, daher ist eine sorgfältige Messung und Auswertung notwendig. In der Wissenschaft gibt es bewährte Methoden und Techniken, um Unsicherheiten und Schwankungen der Messgröße quantitativ zu beschreiben und somit die Qualität der Messung oder des Experiments zu bewerten. Die grundlegenden Normen für die Messtechnik sind in der DIN-Norm DIN 1319 und dem GUM (Guide to the Expression of Uncertainty in Measurement) festgehalten.
Planung: Was soll gemessen werden? Welche Vorbereitungen sind erforderlich? Welche Fehlerquellen oder Störeinflüsse sind zu beachten, und welche systematischen Unsicherheiten sind bekannt?
Durchführung: Führe ein Protokoll! Wurden alle relevanten Informationen sorgfältig dokumentiert und in Tabellen zusammengefasst, notiert oder fotografiert?
Auswertung: Überprüfe die Ergebnisse auf Vollständigkeit und Übersichtlichkeit. Dies umfasst auch eine umfassende Bewertung der Messunsicherheiten.
Überprüfung: Ergeben die Ergebnisse Sinn und stimmen sie mit den Erwartungen überein? Sind sie konsistent mit anderen Ergebnissen in der Literatur?
Präsentation: Stelle die Messergebnisse vollständig dar, einschließlich des Messwerts, der Maßeinheit und der Messunsicherheit. Verwende die wissenschaftliche Notation für Potenzen von Zehn.
Datenauswertung#
Während des Praktikums werdet ihr Daten aufnehmen, auswerten und grafisch darstellen müssen. Verwendet dafür eine geeignete Software, die die Datenanalyse und Fit-Analysen unterstützt. In diesem Kurs werden Beispiele in Python gezeigt, und wir verwenden Jupyter Notebooks. Alternativ könnt ihr auch Qti-Plot (kostenlos) oder Matlab (Lizenzen über die HSU verfügbar) nutzen.
Python: Kostenlos verfügbar, und die Tutorials im Lecture Book verwenden Python in Form von Jupyter-Notebooks.
Matlab: Lizenzen sind über die HSU erhältlich.
QtiPlot: Kostenlos verfügbar.
Wir raten von der Datenanalyse in Excel ab.
Warnung
Alle Beispiele im Metrology Lecture Book sind Jupyter-Notebooks und verwenden Python. Unter 🐍 Jupyter Notebooks findet ihr eine Sammlung von hilfreichen Jupyter-Notebooks für das Messtechnik-Praktikum.
Programmieren mit Python#
Es gibt zahlreiche Tutorials und Online-Ressourcen, die euch das Erlernen der Python-Programmierung leicht und verständlich ermöglichen. Für die Tutorials sind folgende Grundkenntnisse erforderlich, die ihr innerhalb der Tutorials erlernen könnt:
Anschauliche Diagramme#
Mittels Diagrammen (engl. Plots) werden Messwerte dargestellt. Die folgenden Regeln helfen dabei, dass die Diagramme anschaulich sind und der Betrachter direkt erkennt, worum es geht:
Schriftgröße: Nutze eine gut leserliche Schriftgröße.
Achsenbeschriftung: Beschrifte die Achsen richtig, eindeutig und mit vollständiger Angabe: physikalische Größe und Maßeinheit!
Skalierung: Wähle eine passende Skalierung in 1er-/2er-/5er oder 10er- (Dekaden) Schritten auf den Achsen.
Markierungen:
Wähle eine gute erkennbare Markierung für Messpunkte:
lw=0.4,ms=0.1Wähle eine angebrachte Linienbreite für Kurven:
Titel: Nutze passende Über-/ oder Unterschriften für das Diagramm, insbesondere wenn diese in der Auswertung im Text erwähnt werden.
Anderes: Weitere Punkte und Linien, die nicht gemessen wurden, sondern nur als Hilfe dienen (z.B. Fit-Funktionen, Modelle, Referenzlinien) oder Kommentare sind, sollten besonders gekennzeichnet werden.
Messunsicherheiten: Für Messwerte (in Form von Fehlerbalken), aber auch für Funktionsterme und Ausgleichsgeraden, müssen Messunsicherheiten in den Graphen angegeben werden.
Aufgabe
Im Folgenden ist eine sehr ungünstige Darstellung gewählt, um die Messdaten zu zeigen. Klicke oben auf dieser Webseite auf die Rakete und starte Live Code und optimier die Darstellung des Diagramms. Folgende Hinweise geben wir dir mit auf den Weg:
Änder die Schriftgröße:
plt.rcParams['font.size'] = 4;Lösch die Limitierungen auf den Achsen oder passe sie an:
plt.xlim([1850,2040])plt.ylim([-5,5])
Wähle eine geeignete Achsenbeschriftung (Hinweis: Es handelt sich um Klimadaten von der NASA, die die Jahresmitteltemperaturabweichung in °C über die Jahre zeigen)
plt.xlabel('x')plt.ylabel('y')
Änder die Einträge in der Legende
Messwerte (graue Datenpunkte):
label="Werte"Geglättete Messwerte von der NASA (blau):
label="Irgendeine Kurve von irgendwem berechnet"Fit-Funktion/Modell-Funktion (rot): label=“fit”
Durch die Messdaten (blau) soll eine Ausgleichsgerade (rot, “Fit”) gelegt werden, die möglichst gut den linearen Anstieg ab 1980 darstellt. Änder hierfür die
1880an mehreren Stellen.…
#Benötigte Libraries:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
import seaborn as sns
import time
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
fig = plt.figure(figsize=(9,5)) # Plot-Größe
plt.rcParams['font.size'] = 4; # Schriftgröße
link = 'data/graph.csv' # Beispieldatei mit Klimadaten
global_mean = pd.read_csv(link, header = 1) # Daten einlesen
global_mean["uncertainty"] = 0.25 #Messunsicherheiten abschätzen, hier 0.25K Temperaturgenauigkeit angenommen
# Lineare Regression berechnen:
x=global_mean.loc[global_mean["Year"] >= 1880,"Year"]
y=global_mean.loc[global_mean["Year"] >= 1880,"No_Smoothing"]
y_err = global_mean.loc[global_mean["Year"] >= 1880,"uncertainty"]
model = np.polyfit(x, y, deg=1, w=1/y_err, cov=True) # 1. Wert = Anstieg , 2. Wert = Schnittpunkt mit y-Achse
y_model = model[0][0]*x+model[0][1] # Modell einer linearen Regression
# print(global_mean) # Eingelesene Daten ausgeben
plt.errorbar(global_mean["Year"],global_mean["No_Smoothing"], yerr=global_mean["uncertainty"], ls="-", lw=0.4, marker="s", ms=0.1, color="tab:gray", alpha=0.5, label="Werte");
plt.plot(global_mean["Year"],global_mean["Lowess(5)"], lw=4, color="tab:blue", label="Irgendeine Kurve von irgendwem berechnet");
plt.plot(x,y_model, ls="-", lw=4, color="tab:red", label=f"fit");
plt.xlabel('x')
plt.ylabel('y')
plt.xlim([1850,2040])
plt.ylim([-5,5])
plt.legend();
plt.grid();
# Temperaturanstieg ausgeben:
print(f"Lineares Model Output: {model[0][0]:.3f}°C/Jahr")
Beispiel-Lösung
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
fig = plt.figure(figsize=(9,5)) # Plot-Größe
plt.rcParams['font.size'] = 10; # Schriftgröße
link = 'data/graph.csv' # Beispieldatei mit Klimadaten
global_mean = pd.read_csv(link, header = 1) # Daten einlesen
global_mean["uncertainty"] = 0.25 #Messunsicherheiten abschätzen, hier 0.25K Temperaturgenauigkeit angenommen
# Lineare Regression berechnen:
x=global_mean.loc[global_mean["Year"] >= 1980,"Year"]
y=global_mean.loc[global_mean["Year"] >= 1980,"No_Smoothing"]
y_err = global_mean.loc[global_mean["Year"] >= 1980,"uncertainty"]
model = np.polyfit(x, y, deg=1, w=1/y_err, cov=True) # 1. Wert = Anstieg , 2. Wert = Schnittpunkt mit y-Achse
y_model = model[0][0]*x+model[0][1] # Modell einer linearen Regression
# print(global_mean) # Eingelesene Daten ausgeben
plt.errorbar(global_mean["Year"],global_mean["No_Smoothing"], yerr=global_mean["uncertainty"], ls="-", lw=1, marker="s", ms=3, color="tab:gray", alpha=0.5, label="Werte");
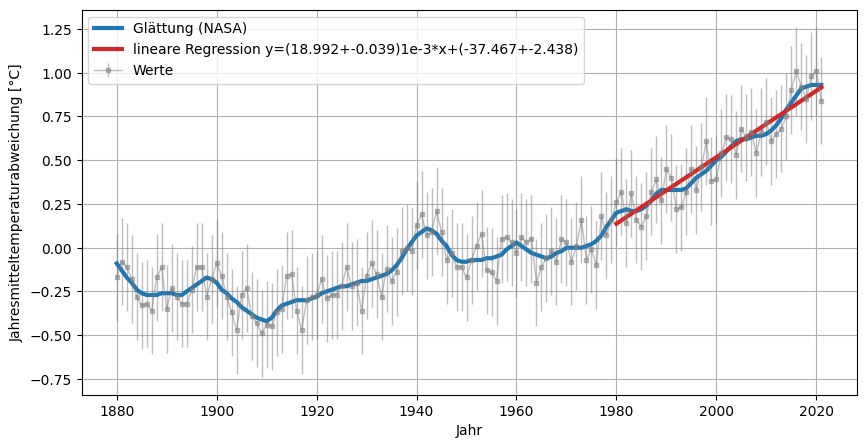
plt.plot(global_mean["Year"],global_mean["Lowess(5)"], lw=3, color="tab:blue", label="Glättung (NASA)");
plt.plot(x,y_model, ls="-", lw=3, color="tab:red", label=f"lineare Regression y=({model[0][0]*1000:.3f}+-{np.sqrt(model[1][0][0]*1000):.3f})1e-3*x+({model[0][1]:.3f}+-{np.sqrt(model[1][1][1]):.3f})");
plt.xlabel('Jahr')
plt.ylabel("Jahresmitteltemperaturabweichung [°C]")
plt.legend();
plt.grid();
# Temperaturanstieg ausgeben:
print(f"Temperaturanstieg pro Jahr (von 1980 bis 2020): {model[0][0]:.3f}°C/Jahr")
