Strommesseingang#
Im Bild Abb. 80 ist dargestellt, wie elektrische Ströme gemessen werden. \(R_L\) stellt hierbei einen Lastwiderstand, z.B. den einen Motors oder eines anderen Verbrauchers, dar.
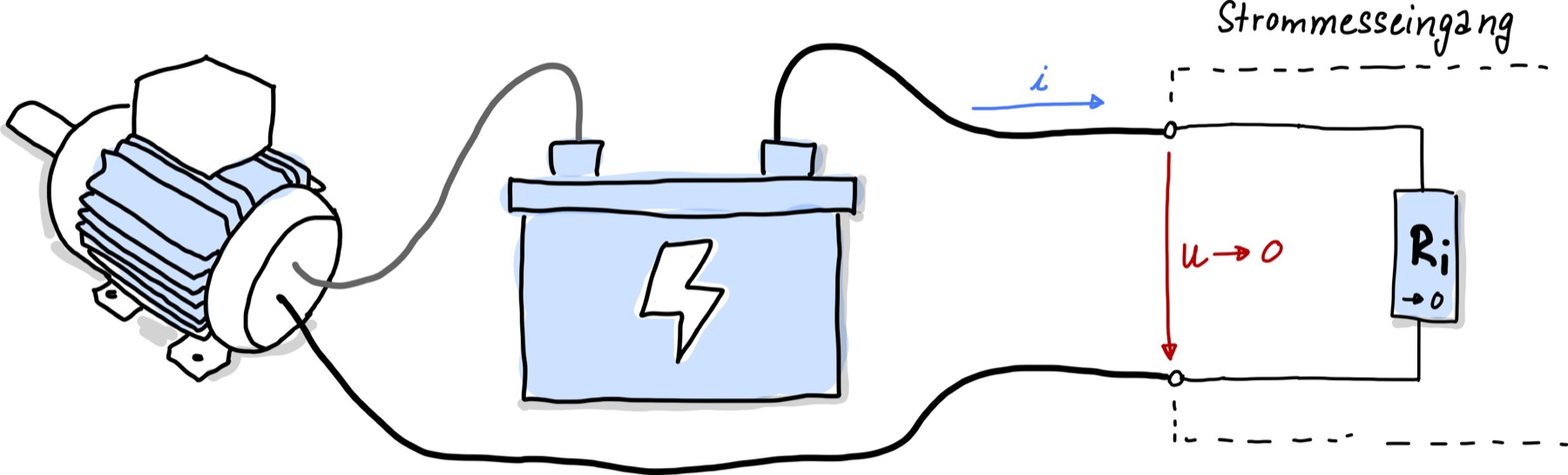
Abb. 80 Schaltung zur Messung elektrischer Ströme.#
Der Strom \(i\), der gemessen werden soll, fließt nun durch das Messgerät und soll bestimmt werden. Hierbei wollen wir sicherstellen, dass der Innenwiderstand \(R_i\) möglichst klein ist, um die Messabweichung der Strommessung möglichst klein zu halten. Typischerweise liegt der Wert des Innenwiderstands zwischen \(0{,}01\,\Omega\) und \(10\,\Omega\). Ein Wert von \(0\,\Omega\) kann in der Praxis nicht erreicht werden. Die kleineren Innenwiderstandswerte werden meist gewählt, wenn es sich um hohe Stromflüsse von mehreren Ampere handelt. Eine Kapazität \(C_i\) ist im Ersatzschaltbild nicht vorhanden. Kapazitäten existieren bei Potentialunterschieden (also elektrische Spannungen) und versuchen diese Unterschiede aufrecht zu erhalten, wodurch eigentlich kein Stromfluss existiert.
Messabweichung#
An unsere Schaltung aus dem letzten Kapitel, bestehend aus zwei Widerständen \(R_1\) und \(R_2\) zu je \(100\,\mathrm{k\Omega}\) schließen wir nun den Strommesseingang an, wie in Abb. 81 dargestellt. Der Innenwiderstand soll \(R_i = 1\,\mathrm{\Omega}\) betragen.
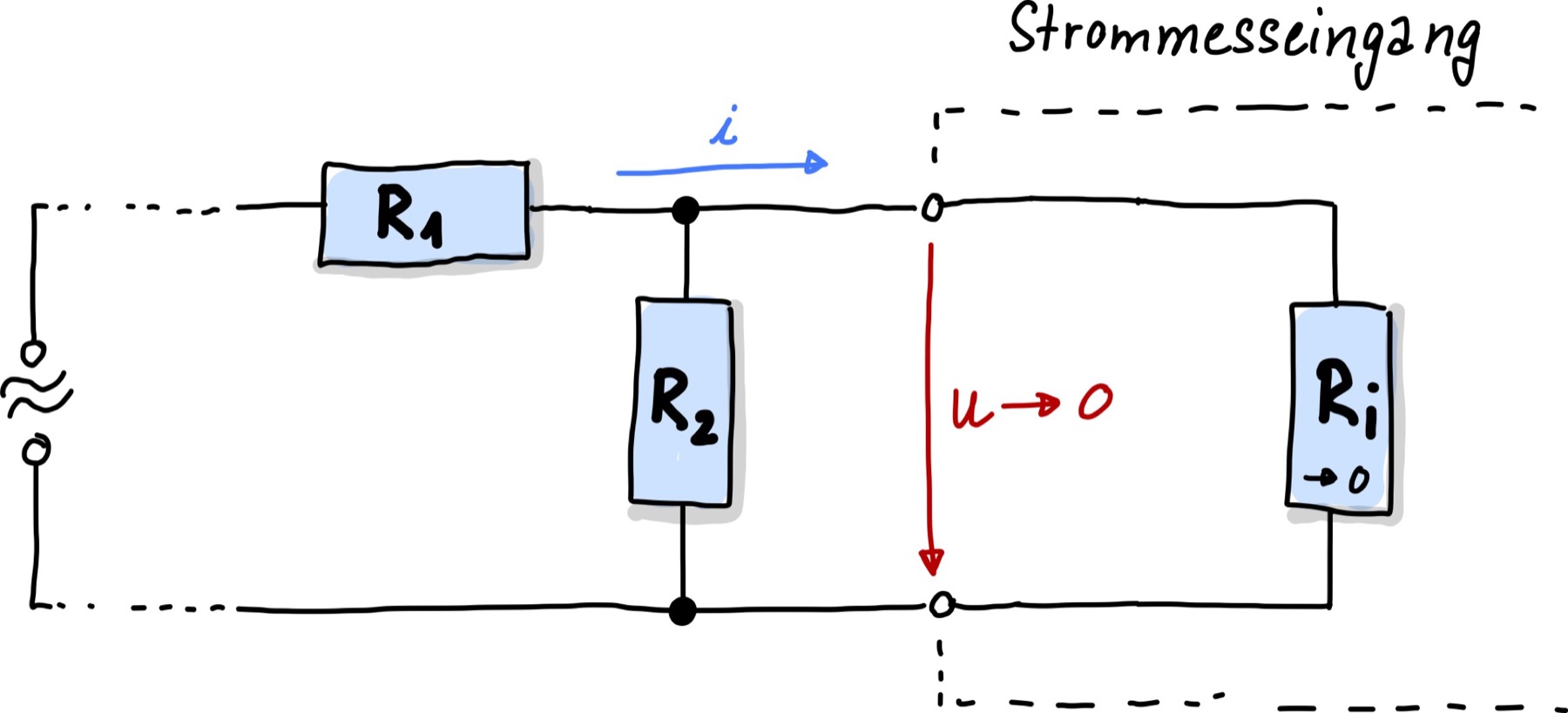
Abb. 81 Strommesseingang an einer Schaltung.#
Der Gesamtwiderstand der Reihenschaltung beträgt nun
Ohne Strommesseingang würde der Gesamtwiderstand der Schaltung
betragen. Die Messabweichung ist wieder abhängig vom Strommesseingang, aber auch von der zu vermessenden Schaltung.
Show code cell source
R_1 = 100 # in Ohm
R_2 = 100 # in Ohm
I_0 = 1 # in Ampere
R_i = 50 # in Ohm
R_0 = R_1 + R_2
R_ges = R_1 + R_2 + R_i
print('Ergebnisse für R_1 =', R_1,'Ohm, R_2 =', R_2, 'Ohm, R_i =', R_i, 'Ohm, I_0 =', I_0, 'A')
print('Die gemessene Stromstärke mit Messeingang: ', R_0/R_ges*I_0, 'A')
print('Die Messabweichung beträgt: ', R_0/R_ges*I_0 - I_0, 'A = ', (1-R_0/R_ges)*100, '%')
Ergebnisse für R_1 = 100 Ohm, R_2 = 100 Ohm, R_i = 50 Ohm, I_0 = 1 A
Die gemessene Stromstärke mit Messeingang: 0.8 A
Die Messabweichung beträgt: -0.19999999999999996 A = 19.999999999999996 %
Die Messabweichung steigt von 0,0005% (\(R_1 = R_2 = 100\,\mathrm{k\Omega}\)) auf fast 0,5% (\(R_1 = R_2 = 100\,\mathrm{\Omega}\)) an, bei einem Innenwiderstand von \(R_i = 1\,\mathrm{\Omega}\). Hat das Messgerät einen schlechten Eingang, also einen höheren Innenwiderstand (\(R_i = 50\,\mathrm{\Omega}\)), wird die Messung noch schlechter und die Messabweichung beträgt nun bereits fast 20%.
Innerer Aufbau#
Bei einem Strommesseingang sind zwei typische Varianten häufig vorzufinden.
Shunt-Widerstand#
Wie in Abb. 82 wird ein kleiner (typischerweise \(1\,\Omega\)) ohmscher Hilfs-Widerstand, der sogenannte Shunt-Widerstand in einem Strommesseingang verwendet.
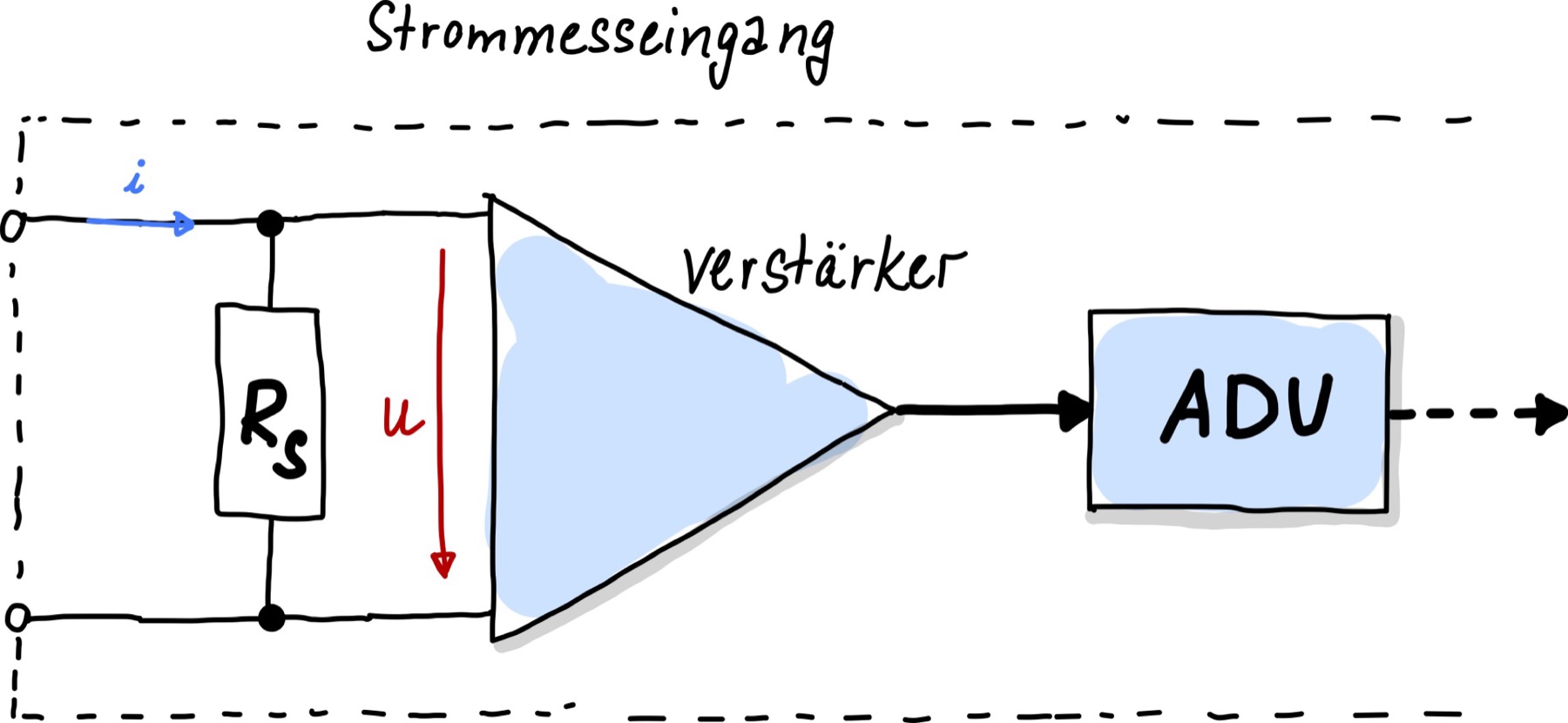
Abb. 82 Strommesseingang mit Shunt-Widerstand \(R_s\). Typische Größenordnungen von Shunt-Widerständen sind \(R_s = 1\,\Omega\).#
Der Strom \(i\), der gemessen werden soll, wird mittels Shunt-Widerstand \(R_s\) in eine Spannung \(u\) umgewandelt:
Die Spannung wird dann mittels Spannungsmesseingang aus dem vorangenenen Kapitel gemessen. Der hohe Innenwiderstand des nachgeschalteten Spannungsmesseingangs ist gegenüber dem kleinen Shunt-Widerstand vernachlässigbar. Die Wahl eines korrekten Wertes für den Shunt-Widerstand ist wichtig und kann unter Umständen auch zu Abweichungen kommen:
Ein hoher Shunt-Widerstandswert liefert einen hohen Spannungswert, was gut für die nachfolgende Spannungsmessung ist. Allerdings ist \(R_s\) gleichzeitig der Innenwiderstand \(R_i\) der Strommessung und sollte eigentlich möglichst kein sein, um die Strommessung \(i\) nicht zu verfälschen.
Als Kompromiss findet man häufig \(R_s \approx 1\,\Omega\).
Der Shunt-Widerstandswert sollte außerdem möglichst genau bekannt sein, da bereits kleinste Abweichung von \(R_s \approx 1\,\Omega\) ansonsten zu verfälschten Ergebnissen führen. Daher verwendet man häufig Präzisionswiderstände. Diese weisen weniger Toleranzen, geringe Fertigungsstreuung und eine kleinere Temperaturabhängigkeit im Vergleich zu üblichen Widerständen auf. Alternativ kann den Widerstandswert vorher auch kalibrieren.
Shunt-Widerstände zur Messung höherer Ströme haben außerdem mehr Anschlüsse, an jedem Ende zwei statt einem. An zwei wird der Strom geleitet, die anderen beiden dienen dem Strommesseingang. Dadurch können Kontaktspannungen, die typischerweise bei den Kontakten abfallen, nach innen verlegt werden und fließen nicht mehr in die Messung mit ein.
Strom-Spannungs-Messumformer#
Die Variante der Strommessung mittels Shunt-Widerstand für Ströme ab \(1\,\mathrm A\) verwendet. Bei kleinere Strömen, oder wenn man eine besonders hohe Messgenauigkeit erreichen möchte, verwendet man eine Verstärkerschaltung, wie in Abb. 82 dargestellt.
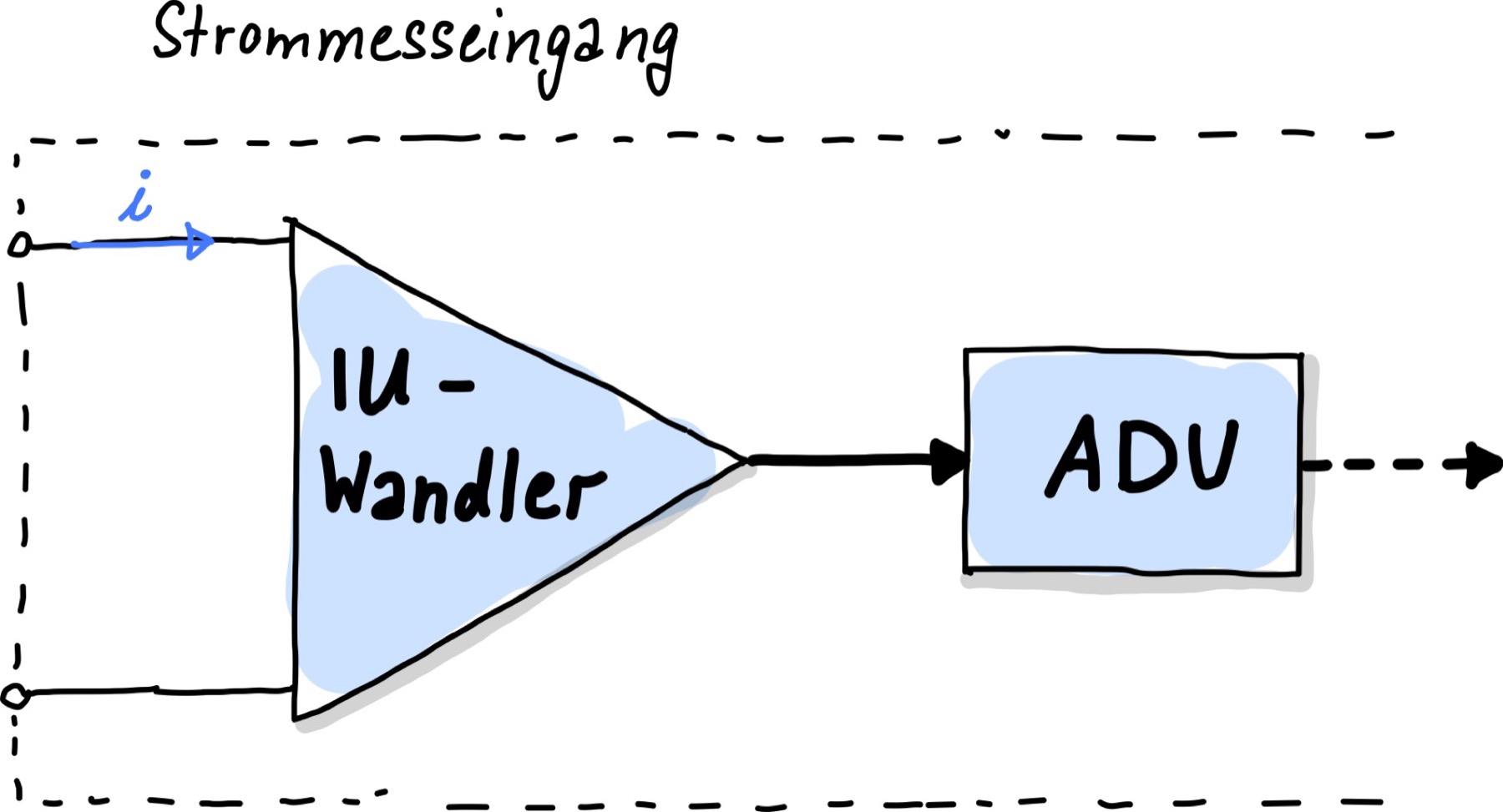
Abb. 83 Strommesseingang mit Strom-Spannungs-Messumformer.#
Der Strom \(i\), der gemessen werden soll, wird zunächst in eine Verstärkerschaltung eingespeist. Die Verstärkerschaltung wandelt Ströme ebenfalls in eine dazu proportional Spannung um. Hierbei handelt es sich meist um sogenannte Operationsverstärker, die aufgrund ihrer Bauweise sehr geringe Innenwiderstände \(R_i\) aufweisen. Dadurch erhält man sehr genaue Strommessungen. Diese Variante ist jedoch auch etwas kostspieliger als die mittels Shunt-Widerstand.
Drehspulmesswerk#
Bei dem Drehspulmesswerk handelt es sich um elektromechanisches Messgerät zur Messung der elektrischen Stromstärke. Es wird eine drehbare Spule auf Kuferdraht in einem Dauermagneten eingebaut. Zwei Spiralfedern dienen der Strumzufuhr und für die Rückstellkraft des Zeigers in seiner Ausgangslage. Der Aufbau ist in Abb. 84 dargestellt. Der Zeiger sollte möglichst starr, leicht und dünn sein, damit der Skalenbereich gut ablesbar ist.
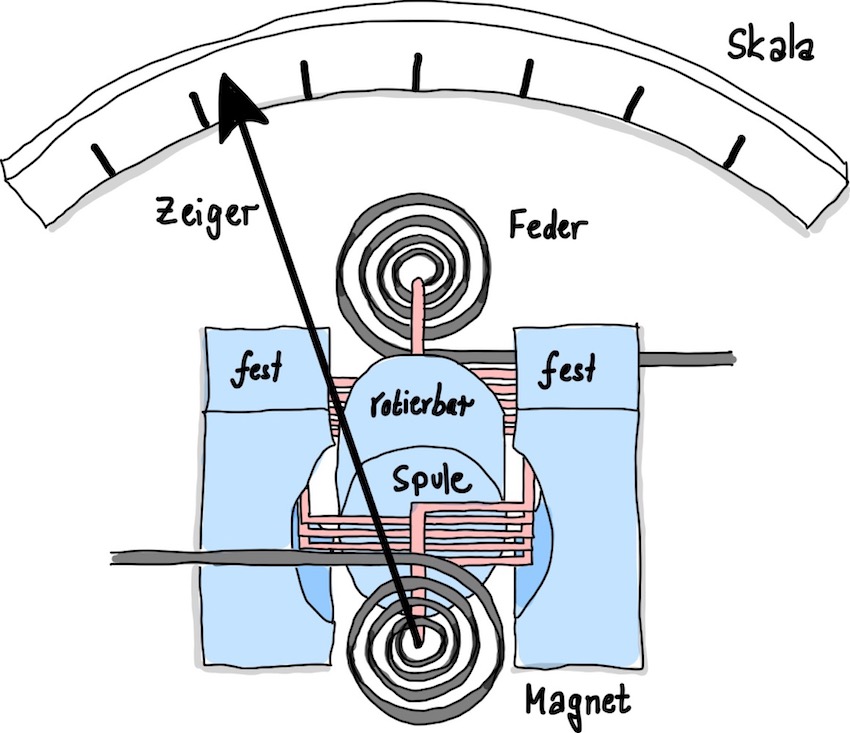
Abb. 84 Aufbau eines Drehspulmesswerk.#
Der zu messende Strom wird nun über die Anschlussklemme und die Federn in die Spule geleitet. Auf die Leiter in der Spule wirkt die Lorentzkraft, wodurch sich der Spulenkörper im Feld des Magneten anfängt zu drehen, wobei die Federkraft dem entgegenwirkt, bis das Drehmoment, \(M_L\), aus der Lorentzkraft, \(F_L\), dem Drehmoment \(M_F\) der Rückstellkraft der Spiralfedern, gleicht:
wobei \(n\) die Windungsanzahl der Spule ist, \(r\) der Radius, \(l\) die Höhe der Spule, \(I\) die Stromstärke, \(B\) die magnetische Flussdichte im Luftspalt, \(D\) die Federkonstante, und \(\alpha\) der Drehwinkel. Nach Gleichsetzen der beiden Gleichung erhält man den Drehwinkel:
mit \(\mathrm{const.} = n\cdot I \cdot B \cdot A / D\), wobei \(A\) die Fläche der Spule ist (\(A = l \cdot 2r\)).
Bei diesem Winkel bleibt die Spule stehen und die Zeigerposition kann auf einer Skala abgelesen werden, was den zugehörigen Stromstärkewert liefert. Wird der Strom wieder abgeschaltet, bringen die Federn den Zeiger zurück in seiner Ausgangslage. Da die Federkraft proportional zum Drehwinkel (hookesches Gesetz) und die Lorentzkraft proportional zur Stromstärke ist, ergibt sich eine linear geteilte Skale über einen Drehwinkel von etwa 90°.
Beim umpolen des Stroms würde der Zeiger in die andere Richtung ausschlagen. Daher können nur Gleichströme gemessen werden. Für Wechselströme wird ein zusätzlicher Gleichrichter benötigt. Außerdem können Stromänderungen aufgrund der Trägheit des Zeigers nur bis zu einer gewissen Rate gemessen werden. Bei Wechselstrom aber einer bestimmten Frequenz (circa ab 10 Hz), wird nur noch der Gleichwert des Stroms angezeigt, also Null.
Dreheisenmesswerk#
Ströme können auch mittels einem Dreheisenmesswerk direkt angezeigt werden. Hierbei handelt es sich um ein analoges Strommessgerät. Es wandelt die Stromstärke direkt in einen Zeigerausschlag um, der entsprechend kalibriert werden muss.
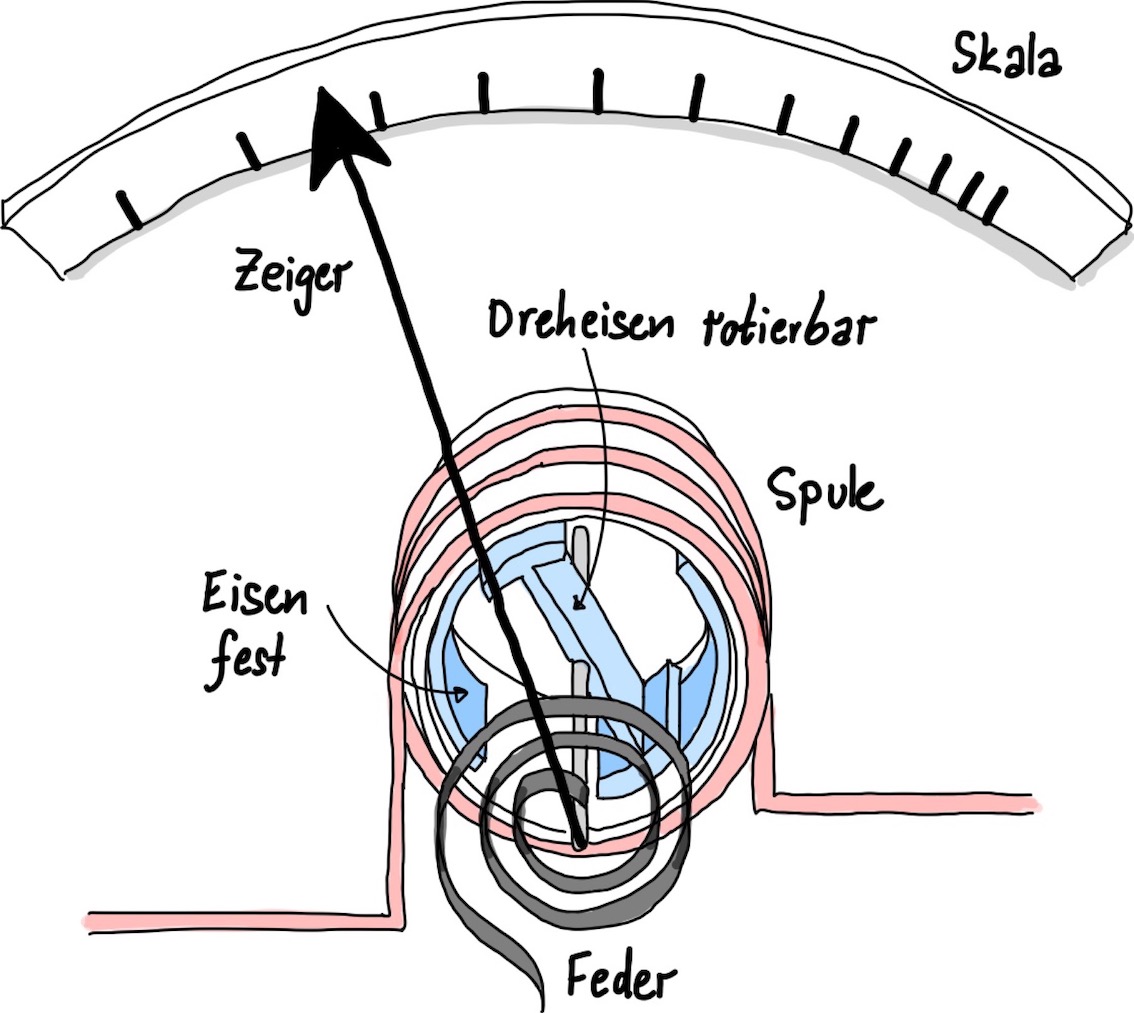
Abb. 85 Aufbau eines Dreheisenmesswerks.#
Hierfür wird eine einzelne Spule benutzt, wie es in Abb. 85 gezeigt ist. Innerhalb dieser Spule befindet sich ein fixierter Eisenkern und ein weiterer beweglicher Eisenkern an der Zeigerachse. Fließt nun ein Strom durch die Spule, so magnetisieren sich die Eisenkernen gleichsinnig und stoßen sich ab. Dadurch kommt es zu einer Rotation des beweglichen Eisenkerns und der Zeiger bewegt sich. Dadurch wird eine Feder gespannt, bis die magnetische Kraft ausgeglichen ist. Wird der Strom abgeschaltet, bringt die Feder den Zeiger zurück in seiner Ausgangslage.
Der Ausschlag ist im Gegensatz zum Zeigerausschlag in einem Drehspulmesswerk nicht mehr proportional sondern hängt von \(I^2\) ab. Dadurch misst das Dreheisenmesswerk den Effektivwert der Stromstärke.
Stromzange#
Eine weitere Möglichkleit Störme zu messen ist die Messung des Magnetfeldes, welches zwangsläufig in einem stromdurchflossenen Leiter hervor gerufen wird. Bei den oben genannten Möglichkeiten muss immer der Stromkreis aufgetrennt werden und das Strommessgerät in den Schaltkreis integriert werden. Die Stromzange ist so aufgebaut, dass der Eisenkern an einer Stelle geöffnet werden kann, wie eine Zangen, und das stromdurchflossene Kabel hindruchgelegt werden kann. Dadurch kann der Strom gemessen werden, ohne dass aktiv in den Stromkreis eingegriffen wird, was eines der großen Vorteile dieses Messprinzips ist. Die Messung erfolgt somit potentialfrei und berührunglos und eignet sich auch zur Messung von Strömen in laufenden Anlagen, ohne die Ausschaltung zu müssen. Einschränkungen ergeben sich nur in der Querschnittsfläche des Leiters, da dieser vollständig von der Stromzangen umschlossen werden muss.
Wechselstrom-Zangenstrommesser#
Mit dem einfachen Prinzip der Stromzange können nur Wechselströme gemessen werden, dies sind sogenannte Wechselstrom-Zangenstrommesser und basieren auf dem Transformator-Prinzip. Dies ist in Abb. 86 dargestellt.
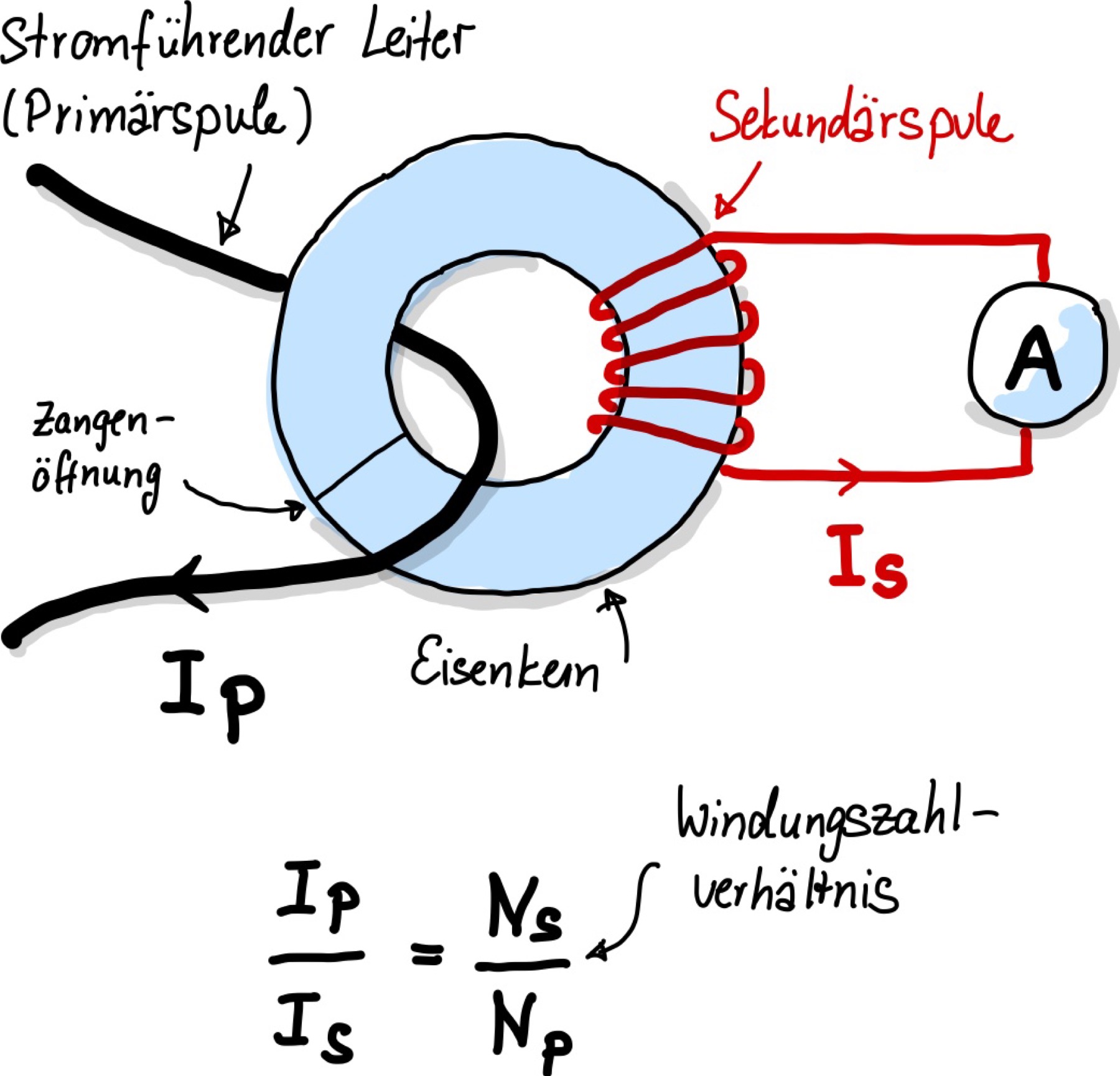
Abb. 86 Darstellung der Strommessung mittels Stromzange für Wechselstrom mittels Sekundärspule.#
Ein Eisenkern fundiert als Trafokern. In diesen Eisenkern wird der stromdurchflossene Leiter eingeführt und bildet eine Spule mit nur einer Windung, die Primärspule. Das Magnetfeld, was durch den stromdurchflossenen Leiter hervor gerufen wird, wird an den Eisenkern übertragen und magnetisiert diesen. Die Magnetisierung induziert in einer Sekundärspule einen Sekundärstrom, der proportional zu dem zu messenden Primärstrom ist. Der Sekundärstrom kann mittels Shunt-Widerstand, Oerationsverstärker oder mit einem Dreheisenmesswerk betrieben gemessen werden kann. Um diese anschließende direkte Stromstärkemessung zu gerantieren wird die Sekundärspulenwicklung direkt so gewählt, dass der resultierende Sekundärstrom groß genug für die folgenden Messgeräte ist. Die Energie zum Antrieb eines Dreheisenmesswerks wird hierbei dem Stromkreis entnommen.
Allstrom-Messer#
Gleichstrom kann mittels dem eben genannten Prinzip nicht gemessen werden, da die Wechselfelder für die Magnetfeldänderungen fehlen. Für Gleichstrommessungen wird der Eisenkern an einer Stelle aufgetrennt und ein Magnetfeld-Sensor (Hall-Sensor oder magnetoresisitiver Widerstand) eingebaut, der auch statische Magnetfelder messen kann und somit nicht auf sich verändernde Wechselfelder angewiesen ist. Dies ist in Abb. 87 dargestellt.
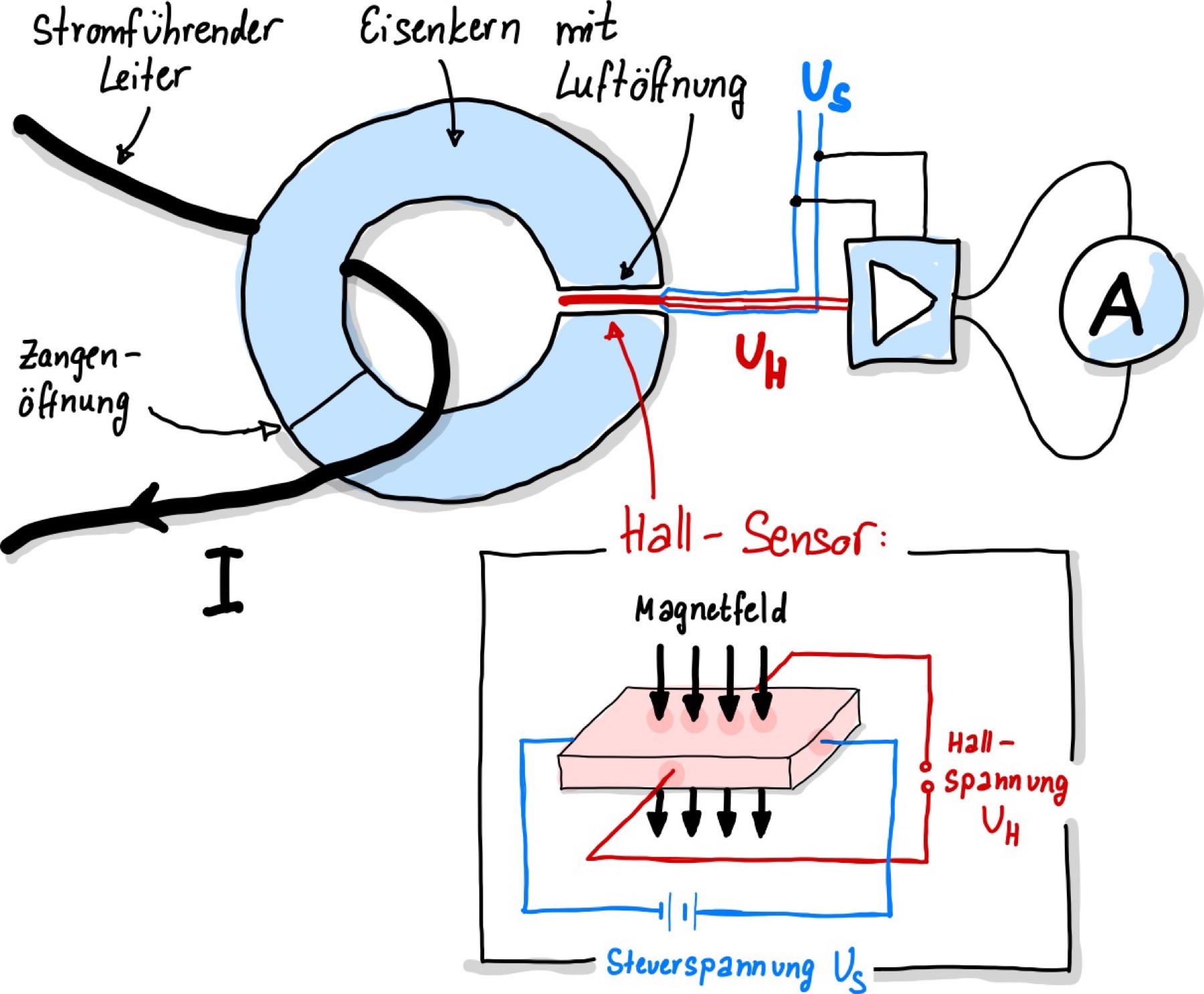
Abb. 87 Darstellung der Strommessung mittels Stromzange auch für Gleichströme, in dem in einem Luftspalt im Eisenkern ein Magnetfeld-Sensor (Hall-Sensor) eingebaut wird, der eine Hall-Spannung generiert.#
Nachteil hierbei ist jedoch, dass nur sehr schwache Signale erzeugt werden, welche elektronisch verstärkt werden müssen. Dafür wird eine zusätzliche Spannungsversorgung benötigt. Wechselströme können allerdings ebenso mit diesem Messgerät gemessen werden.


