Fourier-Analyse#
Fourierreihen#
Jedes periodische Signal kann als Summe von Sinus- und Cosinusfunktionen mit Frequenzen von ganzzahligen Vielfachen der Grundfrequenz des Signals beschrieben werden. Dies ist die sogenannten Fourierreihe, Fourierreihen-Entwicklung/oder -Zerlegung.
Show code cell source
#Benötigte Libraries:
import numpy as np
import pandas as pd
from scipy import signal
import scipy.integrate as spi
import matplotlib.pyplot as plt
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
import time
import warnings
warnings.filterwarnings('ignore')
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
T = 1
t_range = np.linspace(-2*T, 2*T, 1000, endpoint = True)
# Rechteckpuls:
f = lambda t: signal.square(2 * np.pi * 1/T * t)
y_true = f(t_range)
#function that computes the real fourier couples of coefficients (a0, 0), (a1, b1)...(aN, bN)
def compute_real_fourier_coeffs(func, N):
result = []
for n in range(N+1):
an = (2./T) * spi.quad(lambda t: func(t) * np.cos(2 * np.pi * n * t / T), 0, T)[0]
bn = (2./T) * spi.quad(lambda t: func(t) * np.sin(2 * np.pi * n * t / T), 0, T)[0]
result.append((an, bn))
return np.array(result)
#function that computes the real form Fourier series using an and bn coefficients
def fit_func_by_fourier_series_with_real_coeffs(t, AB):
result = 0.
A = AB[:,0]
B = AB[:,1]
for n in range(0, len(AB)):
if n > 0:
result += A[n] * np.cos(2. * np.pi * n * t / T) + B[n] * np.sin(2. * np.pi * n * t / T)
else:
result += A[0]/2.
return result
N = 5
COLs = 2 #cols of plt
ROWs = 1 + (N-1) // COLs #rows of plt
plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(ROWs, COLs)
fig.suptitle('Rechteckpuls')
AB = compute_real_fourier_coeffs(f, N)
y_approx = fit_func_by_fourier_series_with_real_coeffs(t_range, AB)
for n in range(1, N + 1):
row = (n-1) // COLs
col = (n-1) % COLs
axs[row, col].set_title('f=' + str(n) + ' x f_0')
axs[row, col].plot(t_range, AB[:,1][n] * np.sin(2. * np.pi * n * t_range / T))
y_approx = fit_func_by_fourier_series_with_real_coeffs(t_range, AB)
axs[2, 1].plot(t_range, f(t_range),':', color='k', lw = 2)
axs[2, 1].plot(t_range, y_approx, color='tab:red')
axs[2, 1].set_title('Überlagerung der 5 Sinusfunktionen')
plt.tight_layout()
plt.show()
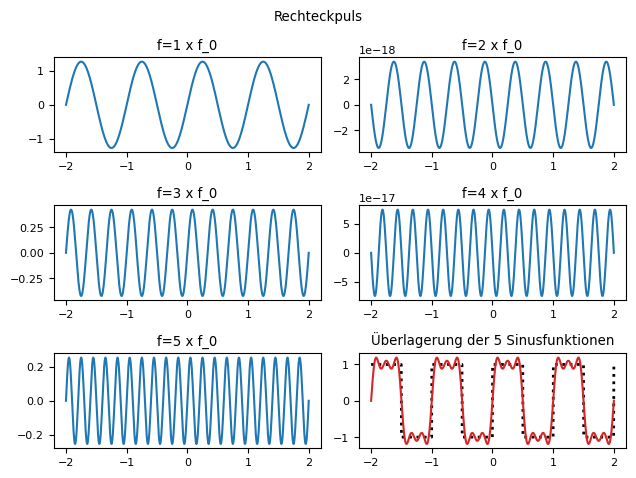
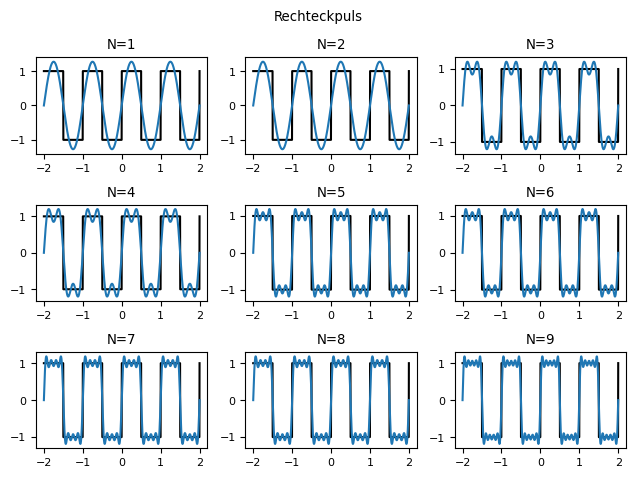
Im folgenden Bild seht ihr einen Rechteckpuls und die zugehörige Fourierreihe unter Einbeziehung verschiedener Anzahl von Sinus- bzw. Cosinusfunktionen. Je mehr Sinusfunktionen bei ganzzahligen Vielfachen der Grundfrequenz des Rechteckpulses miteinbezogen werden, desto genauer können Rechtecksignale rekonstruiert werden.
Show code cell source
#Benötigte Libraries:
import numpy as np
import pandas as pd
from scipy import signal
import scipy.integrate as spi
import matplotlib.pyplot as plt
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
import time
import warnings
warnings.filterwarnings('ignore')
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.figure(figsize=(10,4)) # Plot-Größe
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
T = 1
t_range = np.linspace(-2*T, 2*T, 1000, endpoint = True)
# Rechteckpuls:
f = lambda t: signal.square(2 * np.pi * 1/T * t)
y_true = f(t_range)
#function that computes the real fourier couples of coefficients (a0, 0), (a1, b1)...(aN, bN)
def compute_real_fourier_coeffs(func, N):
result = []
for n in range(N+1):
an = (2./T) * spi.quad(lambda t: func(t) * np.cos(2 * np.pi * n * t / T), 0, T)[0]
bn = (2./T) * spi.quad(lambda t: func(t) * np.sin(2 * np.pi * n * t / T), 0, T)[0]
result.append((an, bn))
return np.array(result)
#function that computes the real form Fourier series using an and bn coefficients
def fit_func_by_fourier_series_with_real_coeffs(t, AB):
result = 0.
A = AB[:,0]
B = AB[:,1]
for n in range(0, len(AB)):
if n > 0:
result += A[n] * np.cos(2. * np.pi * n * t / T) + B[n] * np.sin(2. * np.pi * n * t / T)
else:
result += A[0]/2.
return result
maxN = 9
COLs = 3 #cols of plt
ROWs = 1 + (maxN-1) // COLs #rows of plt
plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(ROWs, COLs)
fig.suptitle('Rechteckpuls')
#fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
#plot, in the range from BT to ET, the true f(t) in blue and the approximation in red
for N in range(1, maxN + 1):
AB = compute_real_fourier_coeffs(f, N)
#AB contains the list of couples of (an, bn) coefficients for n in 1..N interval.
y_approx = fit_func_by_fourier_series_with_real_coeffs(t_range, AB)
#y_approx contains the discrete values of approximation obtained by the Fourier series
row = (N-1) // COLs
col = (N-1) % COLs
axs[row, col].set_title('N=' + str(N))
axs[row, col].plot(t_range, f(t_range), color='k')
axs[row, col].plot(t_range, y_approx, color='tab:blue')
plt.tight_layout()
plt.show()
Reelle Fourierreihe#
Wie berechne ich die nun die benötigten Anteile von Sinus- und Cosinusschwingungen, um eine bestimmte Funktion \(x(t)\) möglichst gut darzustellen? Die reelle Darstellung der Fourierreihe für eine Funktion \(x(t)\) sieht wiefolgt aus:
\(x_0\) ist hierbei der Gleichanteil (Mittelwert) des Signals, der sich wieder über den arithmetischen Mittelwert berechnet:
Die (reellen) Koeffizienten \(a_k\) und \(b_k\) nehmen für jedes Messsignal einen anderen Wert an und berechnen sich über:
und
Jedes Integral muss immer über eine Periode ausgeführt werden. Ob hier die Grenzen \(\pm T/2\) gewählt werden, oder von \(0\) bis \(T\) integriert wird, ist jedem selber überlassen.
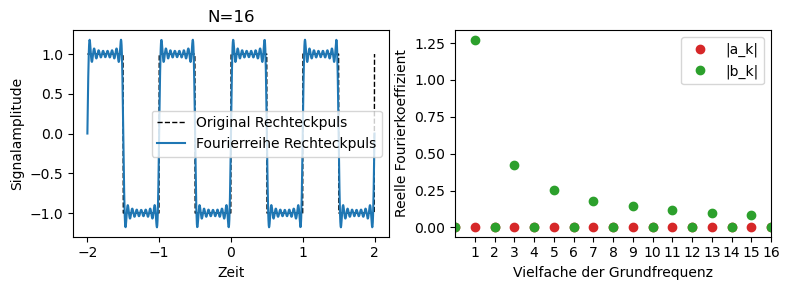
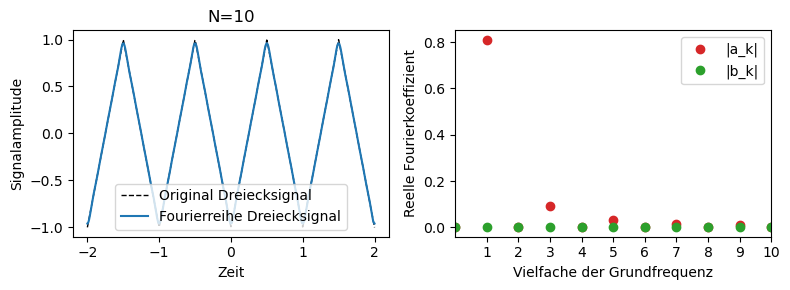
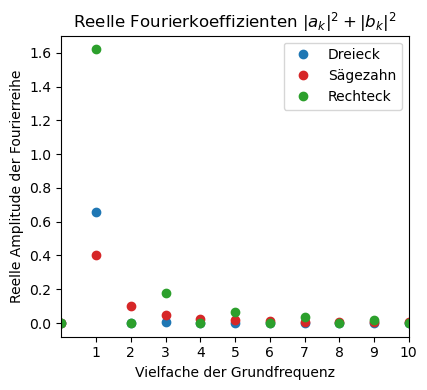
Die Koeffizienten geben die Amplitude der Sinus- bzw. Cosinusfunktionen an, aus denen ein periodisches Signal rekonstruiert wird. Die Koeffizienten werden für die einzelnen Frequenzen berechnet und über die Vielzahl der Grundfrequenz in den folgenden Plots dargestellt. Um eine Rechteckfunktion in einer Fourierreihe zu entwickeln, werden viele höhere Harmonische benötigt. Bei einem Dreickecksignal sieht das anders aus.
Show code cell source
maxN = 16
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
plt.figure(figsize=(8,3)) # Plot-Größe
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
# Rechteckpuls:
f = lambda t: signal.square(2 * np.pi * 1/T * t)
#plot, in the range from BT to ET, the true f(t) in blue and the approximation in red
i = []
for N in range(1, maxN + 1):
i.append(N)
AB = compute_real_fourier_coeffs(f, N)
#AB contains the list of couples of (an, bn) coefficients for n in 1..N interval.
y_approx = fit_func_by_fourier_series_with_real_coeffs(t_range, AB)
#y_approx contains the discrete values of approximation obtained by the Fourier series
plt.subplot(1,2,1)
plt.title('N=' + str(N))
plt.plot(t_range, f(t_range),'--',lw=1, color='k', label = 'Original Rechteckpuls')
plt.plot(t_range, y_approx, color='tab:blue', label = 'Fourierreihe Rechteckpuls')
plt.legend()
plt.xlabel('Zeit')
plt.ylabel('Signalamplitude')
plt.subplot(1,2,2)
plt.plot(abs(AB[:,0]), 'o', color='tab:red', label = '|a_k|')
plt.plot(abs(AB[:,1]), 'o', color='tab:green', label = '|b_k|')
plt.legend()
plt.xlabel('Vielfache der Grundfrequenz')
plt.ylabel('Reelle Fourierkoeffizient')
plt.xticks(i)
plt.xlim([0,N])
plt.tight_layout()
plt.show()
Show code cell source
# Dreieckfunktion:
f = lambda t: signal.sawtooth(2 * np.pi * 1/T * t, 0.5)
maxN = 10
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
plt.figure(figsize=(8,3)) # Plot-Größe
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
#plot, in the range from BT to ET, the true f(t) in blue and the approximation in red
i = []
AB = []
for N in range(1, maxN + 1):
i.append(N)
AB = compute_real_fourier_coeffs(f, N)
#AB contains the list of couples of (an, bn) coefficients for n in 1..N interval.
y_approx = fit_func_by_fourier_series_with_real_coeffs(t_range, AB)
#y_approx contains the discrete values of approximation obtained by the Fourier series
plt.subplot(1,2,1)
plt.title('N=' + str(N))
plt.plot(t_range, f(t_range),'--',lw=1, color='k', label = 'Original Dreiecksignal')
plt.plot(t_range, y_approx, color='tab:blue', label = 'Fourierreihe Dreiecksignal')
plt.legend()
plt.xlabel('Zeit')
plt.ylabel('Signalamplitude')
plt.subplot(1,2,2)
plt.plot(abs(AB[:,0]), 'o', color='tab:red', label = '|a_k|')
plt.plot(abs(AB[:,1]), 'o', color='tab:green', label = '|b_k|')
plt.legend()
plt.xlabel('Vielfache der Grundfrequenz')
plt.ylabel('Reelle Fourierkoeffizient')
plt.xticks(i)
plt.xlim([0,N])
plt.tight_layout()
plt.show()
Aufgabe
Woran könnte es liegen, dass das Rechtecksignal höhere Harmonische benötigt als das Dreiecksignal? Im Python-Code könnt ihr die Flanke des Dreicksignals ändern indem ihr in f = lambda t: signal.sawtooth(2 * np.pi * 1/T * t, 0.5) den letzten Parameter, die 0.5, entfernt. Was ändert sich jetzt?
Es kann übrigens folgendes gezeigt werden, was für die Praxis oft sehr hilfreich ist, da es die Anzahl von Integralberechnungen reduziert:
für gerade Funktionen, also wenn \(x(t) = x(-t)\) gilt, dann sind alle \(b_k = 0\) (es existieren nur noch Cosinus-Terme)
für ungerade Funktionen, also wenn \(x(t) = -x(-t)\) gilt, dann sind alle \(a_k = 0\) (es existieren nur noch Sinus-Terme)
einen Gleichanteil \(x_0\) kann es folglich bei ungeraden Funktionen nicht geben.
Das ist in den obigen Darstellungen bereits zu sehen. Für den Rechteckpuls sind die \(a_k = 0\), während für das Dreiecksignal die \(b_k = 0\) sind.
Komplexe Fourierreihe#
Eine alternative Schreibweise ist die komplexe Darstellung. Hierbei wird eine periodische Funktion als eine Überlagerung von komplexen Exponentialfunktionen (anstelle von Sinus- und Cosinusfunktionen) dargestellt:
Diese liefert den Vorteil, dass nur eine Art von Koeffizienten berechnet werden muss:
Trotz der Rechnung mit komplexen Funktionen handelt es sich immer noch um eine reelle Funktion. Für \(k=0\) erhält man wieder den Gleichanteil:
Außerdem sieht man, dass die Werte für \(\underline {c}_{-k}\) und \(\underline {c}_k\) zueinander komplex konjugiert sind:
Umrechnung zwischen reellen und komplexen Fourier-Koeffizienten#
Mittels der Euler-Formel
lassen sich die Koeffizienten aus reeller Fourierreihen-Entwicklung und komplexer Darstellung ineinander umformen. Durch die Addition eines zueinander komplex konjugierten Koeffizientenpaares lässt sich der reelle Koeffizient \(a_k\) bestimmen:
und analog fällt bei der Subtraktion der Realteil weg, sodass nach zusätzlicher Multiplikation mit \(j\) \(b_k\) berechnet wird:
Andersherum können aus den reellen Koeffizienten auch die komplexen Koeffizienten berechnet werden:
An dieser Stelle wollen wir noch mal festhalten, dass die Koeffizienten der Fourierreihe eine Schwingung oder ein Messsignal im Frequenzbereich eindeutig beschreibt. In Ihrer Gesamtheit stellen diese Koeffizienten das Spektrum des Signals dar. Dies ist zumindest wahr für die hier dargestellte mathematische Betrachtung mittels Fourier-Transformation. Ein Spektrumanalysator wertet hingegen bei der jeder Einzelmessung in einem begrenzten Bereich Frequenzbereich das Signal aus, was häufig noch durch einen Bandpassfilter geschleust wurde. Dabei gehen Informationen über die Phasenlage verloren.
Show code cell source
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
# Dreieckfunktion:
f_drei = lambda t: signal.sawtooth(2 * np.pi * 1/T * t, 0.5)
f_saege = lambda t: signal.sawtooth(2 * np.pi * 1/T * t)
f_eck = lambda t: signal.square(2 * np.pi * 1/T * t)
maxN = 10
plt.rcParams['font.size'] = 10; # Schriftgröße
#plot, in the range from BT to ET, the true f(t) in blue and the approximation in red
i = []
AB_drei = []
AB_saege = []
AB_eck = []
for N in range(1, maxN + 1):
i.append(N)
AB_drei = compute_real_fourier_coeffs(f_drei, N)
AB_saege = compute_real_fourier_coeffs(f_saege, N)
AB_eck = compute_real_fourier_coeffs(f_eck, N)
#AB contains the list of couples of (an, bn) coefficients for n in 1..N interval.
plt.figure(figsize=(8,4)) # Plot-Größe
plt.subplot(1,2,2)
plt.plot(abs(AB_drei[:,0])**2+abs(AB_drei[:,1])**2, 'o', color='tab:blue', label = 'Dreieck')
plt.plot(abs(AB_saege[:,0])**2+abs(AB_saege[:,1])**2, 'o', color='tab:red', label = 'Sägezahn')
plt.plot(abs(AB_eck[:,0])**2+abs(AB_eck[:,1])**2, 'o', color='tab:green', label = 'Rechteck')
plt.legend()
plt.xlabel('Vielfache der Grundfrequenz')
plt.ylabel('Reelle Amplitude der Fourierreihe')
plt.xticks(i)
plt.xlim([0,N])
plt.title(r'Reelle Fourierkoeffizienten $|a_k|^2 + |b_k|^2$')
plt.tight_layout()
plt.show()
Fourier-Transformation#
Die Fourier-Transformation ist Teil der Spektralanalyse in der Messtechnik. Sie basiert auf der Grundidee, dass, wie wir eben gesehen haben, sich jede periodische Funktion aus Sinus- und Cosinusfunktionen schreiben lässt. Das Ziel ist es, die Anteile dieser Schwingungen sichtbar zu machen. Die Fourier-Transformation ist eine mathematische Methode mit der nun auch aperiodische Signale in ein kontinuierliches Spektrum zerlegt werden. Die Fourier-Transformation ist ein Werkzeug, mit dem man ein Signal nehmen und die Leistung jeder einzelnen Frequenz darin sehen kann.
Anwendung#
Eine Spektralanalyse, wie sie die Fouriertransformation durchführt, eignet sich besonders gut zur Zustandsüberwachung. Hier können Motoren, Turbinen, Sägen, Kugellager uvm, im Prinzip alles was rotiert, überwacht werden. Die spezifische Frequenz jedes Kugellagers kann beispielsweise überwacht werden. Sollte sich die Amplitude über die Zeit verändern, kann dies ein Indiz dafür sein, dass eine Kugel ins Lager gefallen ist oder das Lager einen Schaden bekommen hat. Verschlechtert sich das Verhalten kann frühzeitig gegengewirkt werden, indem das Kugellager ausgetauscht wird. Das heißt auch Fehlerfrüherkennung, Fehlerdiagnose und Trendanalysen (“predictive maintenance”) werden häufig im Frequenzraum durchgeführt.
Shazam und andere Musikerkennungsdienste verwenden beispielsweise die Fourier-Transformation, um Lieder zu erkennen. Bei der JPEG-Komprimierung wird eine Variante der Fourier-Transformation verwendet, um die hochfrequenten Komponenten von Bildern zu entfernen. Bei der Spracherkennung werden die Fourier-Transformation und verwandte Transformationen verwendet, um die gesprochenen Wörter aus dem Audiomaterial wiederherzustellen.
Im Allgemeinen benötigst du die Fourier-Transformation, wenn du die Frequenzen in einem Signal betrachten musst. Wenn die Arbeit mit einem Signal im Zeitbereich schwierig ist, lohnt es sich, die Fourier-Transformation zu verwenden, um es in den Frequenzbereich zu übertragen. Im nächsten Abschnitt werden Sie die Unterschiede zwischen dem Zeit- und dem Frequenzbereich kennen lernen.
Zeit- vs. Frequenzbereich#
Du wirst im Folgenden immer wieder auf die Begriffe Zeitbereich und Frequenzbereich stoßen. Diese beiden Begriffe beziehen sich auf zwei verschiedene Arten der Betrachtung eines Signals, entweder als seine Frequenzkomponenten oder als Information, die sich über die Zeit verändert. Im Folgenden sehen wir uns an, wie ein Audiosignal im Zeit- bzw. Frequenzbereich aussieht. Hierfür benutzen wir das Audiosignal, was sich wiefolgt anhört:
Show code cell source
import IPython.display as ipd
ipd.Audio('CantinaBand3.wav') # load a local WAV file
Show code cell source
from scipy.fft import rfft, rfftfreq
from scipy.io.wavfile import read #import the required function from the module
import matplotlib.pyplot as plt
import numpy as np
samplerate, y = read('CantinaBand3.wav')
duration = len(y)/samplerate
time = np.arange(0,duration,1/samplerate) #time vector
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
plt.figure(figsize=(8,3)) # Plot-Größe
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
y_normalized = np.int16((y / y.max()) * 32767)
# Note the extra 'r' at the front
yf = rfft(y_normalized)/5e6
xf = rfftfreq(len(y), 1 / samplerate)
plt.subplot(1,2,1)
plt.plot(time,y, 'tab:blue')
plt.xlabel('Zeit (s)')
plt.ylabel('Amplitude')
plt.title('Audio-Signal im Zeitbereich')
plt.subplot(1,2,2)
plt.plot(xf,np.abs(yf),'tab:red') # plotting the spectrum
plt.xlabel('Frequenz (Hz)')
plt.ylabel('Leistung')
plt.title('Audio-Signal im Frequenzbereich')
plt.tight_layout()
plt.show()
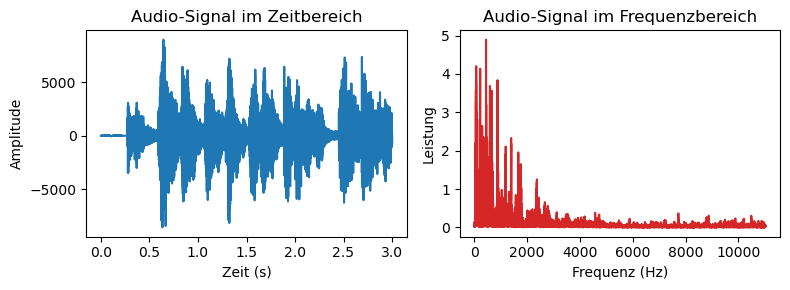
Das Bild links zeigt das aperiodische Zeitsignal, das Bild rechts das Signal nach der Fourier-Transformation. Jeder Frequenz entlang der x-Achse ist eine Leistung zugeordnet, wodurch das Spektrum entsteht.
Typen von Fourier-Transformationen#
Die Fourier-Transformation kann in verschiedene Arten von Transformationen unterteilt werden. Die grundlegendste Unterteilung basiert auf der Art der Daten, mit denen die Transformation arbeitet: kontinuierliche Funktionen oder diskrete Funktionen. Die Begriffe DFT und FFT werden oft synonym verwendet. Sie sind jedoch nicht ganz dasselbe. Die fast (kontinuierliche) Fourier-Transformation (FFT) ist ein Algorithmus zur Berechnung der diskreten Fourier-Transformation (DFT), während die DFT die Transformation selbst ist.
Die diskrete Fourier-Transformation (DFT) (z.B. auf digitalisierte, abgetastete Messwerte angewendet) entspricht der Fourierreihen:
wobei \(\Delta f = 1/T\) mit der Periode \(T = N\cdot \Delta T\), \(N\) ist die Anzahl der Samples.
Die kontinuierliche Fourier-Transformation ist für beliebige Funktionen \(f(t)\) definiert, d.h. die Periode kann unendlich lang werden und die Funktion kann aperiodisches Verhalten aufweisen:
Die Rücktransformation ist wie folgt definiert:
Der Vollständigkeits halber soll an dieser Stelle auch noch die Laplace-Transformation erwähnt werden, die sich wie folgt berechnen lässt:
mit der Rücktransformation
Hierbei ist \(s= \sigma + j\omega\) eine komplexe Zahl (anstelle von \(\omega\)) und wird für dynamische Messsysteme wichtig werden.
Eigenschaften#
Jede Fourier-Transformation hat folgende wichtige Eigenschaften, die das Leben und Rechnen im Frequenzraum erheblich erleichtern können:
Linearität: \(\mathcal F(ax_1 + bx_2) = a\mathcal F(x_1)+ b \mathcal F(x_2)\)
Ableitung: \(\mathcal F(\dot x) = j\omega \cdot \mathcal F(x)\)
Faltung:\( \mathcal F(x_1*x_2) = \mathcal F(x_1) \cdot \mathcal F(x_2)\)
Faltung im Zeichbereich ist zum Vergleich sehr kompliziert: \((x_1 \ast x_2)(t) = \int_{-\infty}^{\infty} x_1(\tau)x_2(t-\tau) \mathrm{d}\tau\)
Zeitverschiebung: \(\mathcal F(x(t-\tau)) = \mathcal F(x(t)) \cdot \mathrm e^{-j\omega \tau}\)
Integral: \(\mathcal F(\omega = 0)\) liefert das Integral der Funktion im Zeitbereich.
Fourier-Transformation eines Rechteckpulses#
Es sei eine Rechteckfunktion mit Amplitude 1 und der Breite \(T=2\tau\) gegeben:
Für die Fourier-Tranformierte folgt:
wobei wir im 2. Schritt angenommen haben, dass \(h(t)\) reell und gerade ist und die Euler-Formel (\(\mathrm e^{j\omega t} = \cos(\omega t) + j\sin(\omega t)\)) entsprechend vereinfachen konnten. In der dritten Zeile wurde mit \(\tau/\tau\) erweitert und substitutiert (\(\tau = T/2\), \(\omega = 2\pi f\)).
Folgende Eigenschaften gelten:
\(H(f = 0)\) ist gleich der Fläche unter dem Rechteck, also gleich dem Integral der Rechteckfunktion.
Die Nulldurchgänge von \(H(f)\) sind bei \(\pi T f_n = n \pi\), für \(\lvert n \rvert = 1,2,3...\)
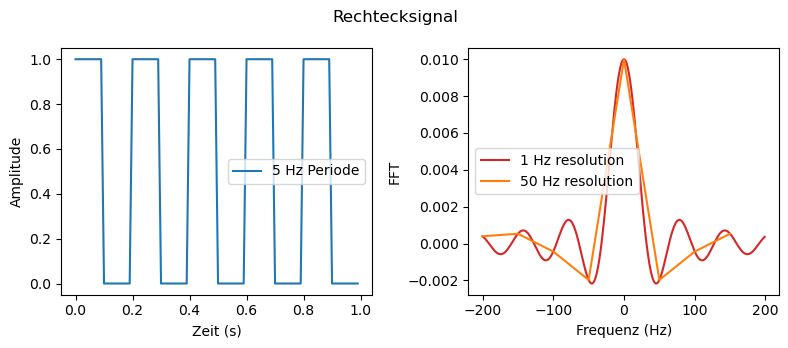
Es gilt also \(f_n = n/T\). Für \(n=1\) sieht man, dass je kürzer der Rechteckpuls ist, desto breiter (unschärfer) wird das Spektrum (Unschärferelation der Fourier-Transformation)
Show code cell source
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
# Rechteckschwingung
Fs = 100.0; # sampling rate
Ts = 1.0/Fs; # sampling interval
t = np.arange(0,1,Ts) # time vector
ff = 5; # frequency of the signal
maxN = int(Fs/2)
# Sinusschwingung
f = lambda t: (signal.square(2 * np.pi * ff * t) + 1)*0.5
y = f(t)
F_end = 200
BW = 1
f1 = np.arange(-F_end,F_end,BW) # time vector
BW = 50
f10 = np.arange(-F_end,F_end,BW) # time vector
plt.figure(figsize=(8,3.5)) # Plot-Größe
plt.subplot(1,2,1)
plt.plot(t,y, label = '5 Hz Periode')
plt.legend()
plt.xlabel('Zeit (s)')
plt.ylabel('Amplitude')
plt.subplot(1,2,2)
plt.plot(f1,Ts * np.sinc(np.pi * Ts * f1),'tab:red', label = '1 Hz resolution') # plotting the spectrum
plt.plot(f10,Ts * np.sinc(np.pi * Ts * f10),'tab:orange', label = '50 Hz resolution') # plotting the spectrum
plt.xlabel('Frequenz (Hz)')
plt.ylabel('FFT')
plt.suptitle('Rechtecksignal')
plt.legend()
plt.tight_layout()
plt.show()
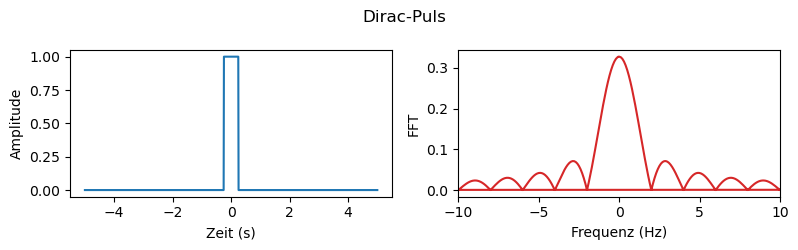
Dirac-Delta-Impuls#
Wir können den klassischen Rechteckpuls nun anpassen. Die Höhe beträgt statt 1 nun \(1/2\tau\):
wodurch die Fläche unter dem Quadrat nun 1 wird. Für die Fourier-Transformierte gilt:
Der Grenzwert, \(\tau \rightarrow 0\) führt direkt zu der Definition des Dirac-Delta-Impuls:
Dirac-Delta-Impuls hat folgende Eigenschaften:
Das Integral ist 1: \(\int_{-\infty}^{\infty} \delta(t) dt = 1\)
Die Fourier-Transformierte ist: \(\int_{-\infty}^{\infty} \delta(t) \mathrm e^{-j \omega t} dt = 1\)
Mit \(g(\tau) = \mathrm e^{-j \omega t}\) kann der Delta-Impuls wiefolgt definiert werden: \(\int_{\infty}^{\infty} \delta(0-\tau)g(\tau) d\tau = g(0)\)
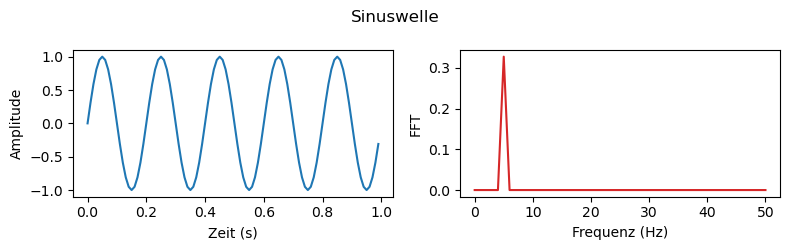
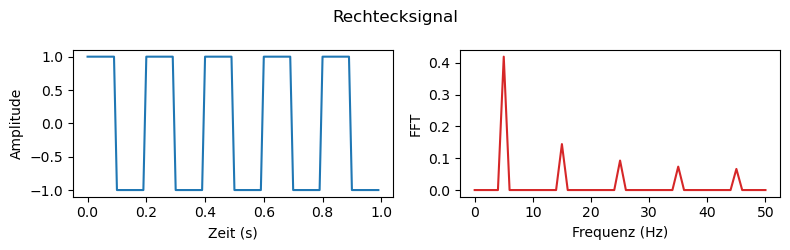
Fourier-Transformierte von Messsignalen#
Show code cell source
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
Fs = 100.0; # sampling rate
Ts = 1.0/Fs; # sampling interval
t = np.arange(0,1,Ts) # time vector
ff = 5; # frequency of the signal
maxN = int(Fs/2)
# Sinusschwingung
f = lambda t: np.sin(2*np.pi*ff*t)
y = f(t)
y_normalized = np.int16((y / y.max()) * 32767)
# Note the extra 'r' at the front
yf = rfft(y_normalized)/5e6
xf = rfftfreq(len(y), 1 / Fs)
plt.figure(figsize=(8,2.5)) # Plot-Größe
plt.subplot(1,2,1)
plt.plot(t,y, 'tab:blue')
plt.xlabel('Zeit (s)')
plt.ylabel('Amplitude')
plt.subplot(1,2,2)
plt.plot(xf,abs(yf),'tab:red', label = 'FFT') # plotting the spectrum
plt.xlabel('Frequenz (Hz)')
plt.ylabel('FFT')
plt.suptitle('Sinuswelle')
plt.tight_layout()
plt.show()
Show code cell source
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
# Rechteckschwingung
Fs = 100.0; # sampling rate
Ts = 1.0/Fs; # sampling interval
t = np.arange(0,1,Ts) # time vector
ff = 5; # frequency of the signal
maxN = int(Fs/2)
# Sinusschwingung
f = lambda t: signal.square(2 * np.pi * ff * t)
y = f(t)
y_normalized = np.int16((y / y.max()) * 32767)
# Note the extra 'r' at the front
yf = rfft(y_normalized)/5e6
xf = rfftfreq(len(y), 1 / Fs)
plt.figure(figsize=(8,2.5)) # Plot-Größe
plt.subplot(1,2,1)
plt.plot(t,y)
plt.xlabel('Zeit (s)')
plt.ylabel('Amplitude')
plt.subplot(1,2,2)
plt.plot(xf,abs(yf),'tab:red', label = 'FFT') # plotting the spectrum
plt.xlabel('Frequenz (Hz)')
plt.ylabel('FFT')
plt.suptitle('Rechtecksignal')
plt.tight_layout()
plt.show()
Show code cell source
from scipy.fft import fft, fftfreq
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
def ddf(x,sig):
val = np.zeros_like(x)
val[(-(1/(2*sig))<=x) & (x<=(1/(2*sig)))] = 1
return val
X=np.linspace(-5,5,1000)
y = ddf(X,2.)
y_normalized = np.int16((y / y.max()) * 32767)
# Note the extra 'r' at the front
yf = fft(y_normalized)/5e6
xf = fftfreq(len(y), 1 / Fs)
plt.figure(figsize=(8,2.5)) # Plot-Größe
plt.subplot(1,2,1)
plt.plot(X,y, 'tab:blue')
plt.xlabel('Zeit (s)')
plt.ylabel('Amplitude')
plt.subplot(1,2,2)
plt.plot(xf,abs(yf),'tab:red', label = 'FFT') # plotting the spectrum
plt.xlabel('Frequenz (Hz)')
plt.ylabel('FFT')
plt.xlim(-10,10)
plt.suptitle('Dirac-Puls')
plt.tight_layout()
plt.show()
Show code cell source
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
Fs = 100.0; # sampling rate
Ts = 1.0/Fs; # sampling interval
t = np.arange(0,1,Ts) # time vector
ff = 5; # frequency of the signal
maxN = int(Fs/2)
# Sinusschwingung
f = lambda t: signal.sawtooth(2 * np.pi * ff * t, 0.5)
y = f(t)
y_normalized = np.int16((y / y.max()) * 32767)
# Note the extra 'r' at the front
yf = rfft(y_normalized)/5e6
xf = rfftfreq(len(y), 1 / Fs)
plt.figure(figsize=(8,2.5)) # Plot-Größe
plt.subplot(1,2,1)
plt.plot(t,y)
plt.xlabel('Zeit (s)')
plt.ylabel('Amplitude')
plt.subplot(1,2,2)
plt.plot(xf,abs(yf),'tab:red', label = 'FFT') # plotting the spectrum
plt.xlabel('Frequenz (Hz)')
plt.ylabel('FFT')
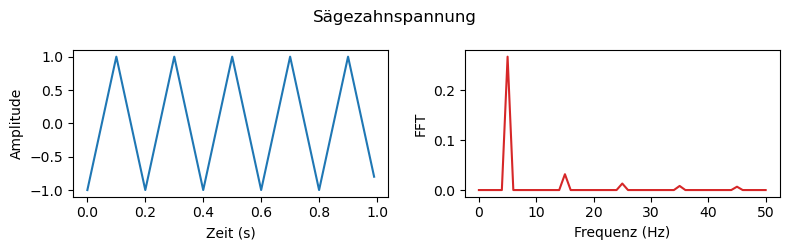
plt.suptitle('Sägezahnspannung')
plt.tight_layout()
plt.show()
Show code cell source
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
Fs = 150.0; # sampling rate
Ts = 1.0/Fs; # sampling interval
t = np.arange(0,1,Ts) # time vector
ff = 5; # frequency of the signal
a1 = 4.
a2 = 2.
y = a1 * np.sin(2 * np.pi * ff * t) + a2 * np.sin(10 * 2 * np.pi * ff * t)
y_normalized = np.int16((y / y.max()) * 32767)
yf = rfft(y_normalized)/5e6
xf = rfftfreq(len(y), 1 / Fs)
plt.figure(figsize=(8,2.5)) # Plot-Größe
plt.subplot(1,2,1)
plt.plot(t,y)
plt.xlabel('Zeit (s)')
plt.ylabel('Amplitude')
plt.subplot(1,2,2)
plt.plot(xf,abs(yf),'tab:red') # plotting the spectrum
plt.xlabel('Frequenz (Hz)')
plt.ylabel('FFT')
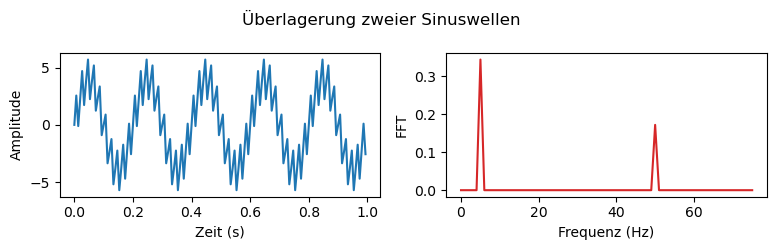
plt.suptitle('Überlagerung zweier Sinuswellen')
plt.tight_layout()
plt.show()
Show code cell source
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['font.size'] = 10; # Schriftgröße
Fs = 150.0; # sampling rate
Ts = 1.0/Fs; # sampling interval
t = np.arange(0,1,Ts) # time vector
ff = 5; # frequency of the signal
## --- White noise generation ---------------------------------
y_wn_0 = np.random.normal(scale=2, size=t.shape)
y_wn_1 = np.random.normal(scale=2, size=t.shape)
y_wn_2 = np.random.normal(scale=2, size=t.shape)
a1 = 4.
a2 = 2.
y = a1 * np.sin(2 * np.pi * ff * t) + a2 * np.sin(10 * 2 * np.pi * ff * t)
a_wn = 1.0
a_f1 = 1.0
wn= y_wn_0*a_wn # white noise
fn1 = np.cumsum(y_wn_1)/Fs*a_f1 # 1/f noise
combined = y+wn+fn1
y_normalized = np.int16((combined / combined.max()) * 32767)
yf = rfft(y_normalized)/5e6
xf = rfftfreq(len(y), 1 / Fs)
plt.figure(figsize=(8,2.5)) # Plot-Größe
plt.subplot(1,2,1)
plt.plot(t,combined)
plt.xlabel('Zeit (s)')
plt.ylabel('Amplitude')
plt.subplot(1,2,2)
plt.plot(xf,abs(yf),'tab:red') # plotting the spectrum
plt.xlabel('Frequenz (Hz)')
plt.ylabel('FFT')
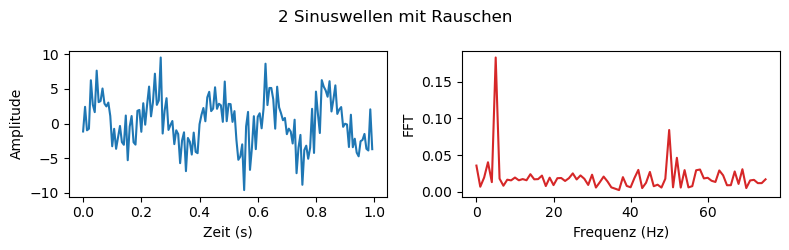
plt.suptitle('2 Sinuswellen mit Rauschen')
plt.tight_layout()
plt.show()
Vergleich der Varianten von Fourier-Analysen#
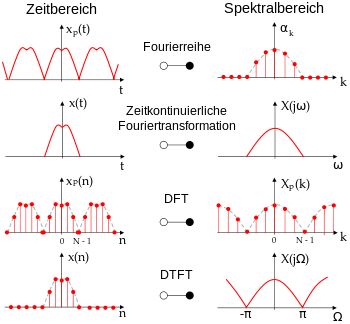
Abb. 49 Fourier-Analyse (https://www.biancahoegel.de/mathe/analysis/fourieranalysis.html)#
Periodische Funktion in einem endlichen Intervall: Fourier-Reihe (diskretes Spektrum)
Aperiodischer Funktion in unendlichem Intervall: kontinuierliche Fourier-Transformation (kontinuierliches Spektrum)
Diskrete Werte an äquidistanten Zeitpunkten in einem endlichen Intervall - durch Intervallbildung besteht aber periodische Fortsetzung: Diskrete Fourier-Transformation (diskretes Spektrum mit Spiegelspektren)
DTFT (Fouriertransformation für zeitdiskrete Signale (englisch discrete-time Fourier transform, DTFT)) ist wie DFT, bildet aber kontinuierliches Spektrum ab (theoretische Analyse, hier lässt sich das Spektrum als ein mathematischer Ausdruck angeben)
Referenztabellen für die Laplace-Transformation#
\(\sigma(t)\) ist die Sprungfunktion und \(\delta(t)\) der Delta-Dirac-Puls.
Originalfunktion \(u(t)\) |
Bildfunktion \(U(s)\) |
|---|---|
\(\delta(t)\) |
\(1\) |
\(\sigma(t)\) |
\(\frac{1}{s}\) |
\(\mathrm e^{-at} h(t)\) |
\(\frac{1}{s+a}\) |
\(\cos(\omega_0 t)\) |
\(\frac{s}{s^2 + \omega_0^2}\) |
\(\sin(\omega_0 t)\) |
\(\frac{\omega_0}{s^2 + \omega_0^2}\) |
\((1-\mathrm e^{-at}) h(t)\) |
\(\frac{a}{s(s+a)}\) |
\(\mathrm e^{-at} \cos(\omega_0 t)\) |
\(\frac{s+a}{(s+a)^2 + \omega_0^2}\) |
\(\mathrm e^{-at} \sin(\omega_0 t)\) |
\(\frac{\omega_0}{(s+a)^2 + \omega_0^2}\) |
\(\delta(t)t\) |
\(\frac{1}{s^2}\) |


