Operationsverstärker (OP)#

Liegen kleine Signale vor, wie z.B. kleine Stromstärken \(I\), Spannungswerte \(U\) oder Widerstandswerte \(R\), so werden die Signale häufig als erstes verstärkt, was mittels einem Operationsverstärker (OP) realisiert wird. In Abb. 86 ist eine schematische Zeichnung eines OPs dargestellt.

op

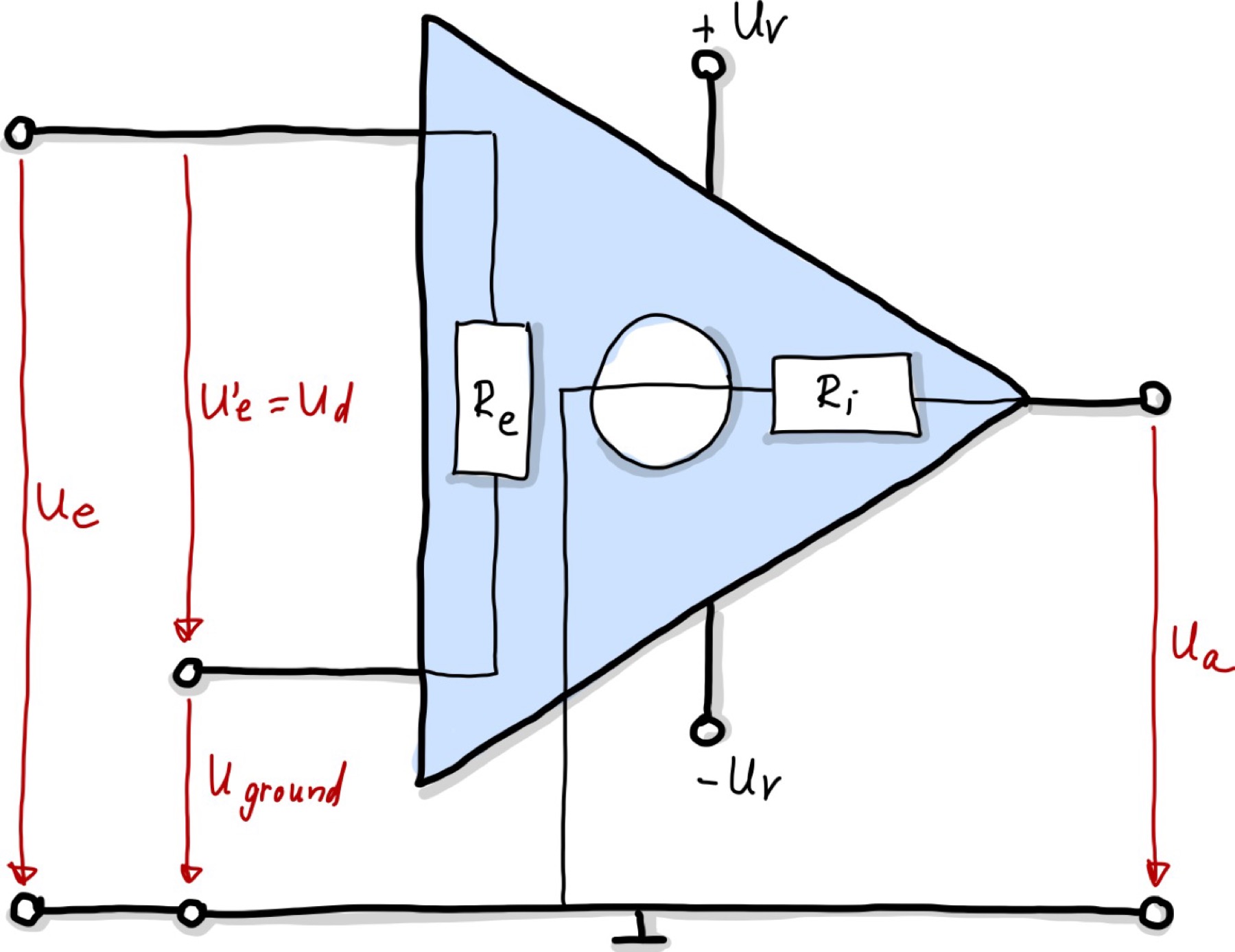
Abb. 86 Schematische Darstellung eines Operationsverstärkers (OPs) mit Eingangs-Innenwiderstand \(R_e\), Ausgangs-Innenwiderstand \(R_i\) und Spannungsversorgung \(U_V\). \(U_d\) ist die angelegte Eingangsspannung an dem differentiellen Eingang des OPs. \(U_a\) ist die Ausgangsspannung.#

Eigenschaften#

Dies sollte möglichst rückwirkungsfrei geschehen, das heißt dass die Verstärkerschaltung möglichst wenig Einfluss auf die Messgröße und die weiterführende Signalverarbeitung hat. Für eine Spannung, die man anlegt, sollte der Eingangs-Innenwiderstand \(R_e\) also möglichst groß sein, um den kompletten Spannungsabfall zu messen. Typische reale Werte liegen zwischen \(R_e' \approx 10^6 - 10^{12}\,\mathrm{\Omega}\). Der Innenwiderstandswert eines idealen OPs wäre \(R_e = \infty\).

Desweiteren möchte man eine hohe Empfindlichkeit und eine große Verstärkung erreichen, weshalb eine zusätzliche Strom- bzw. Spannungsversorgung \(U_V\) von Nöten ist, da die zusätzlich Energie von Außen dem System zugeführt werden muss. Dies ist der allgemein Sinn von Operationsverstärkern. Die Verstärkung ist allgemein definiert als

\[ k' = \frac{U_\mathrm a}{U_\mathrm d} \]

wobei \(k'\) die reale Verstärkung des OPs ist, \(k\) wäre die des idealen OPs (\(k = \infty\)) und \(U_\mathrm a\) ist die Ausgangsspannung und \(U_\mathrm d\) die differentielle Eingangsspannung. Reale Verstärkungsfaktoren liegen in der Größenordnung von \(k' \approx 10^6\).

Das Ausgangssignal sollte weiterdessen direkt mit dem Eingangssignal korreliert sein, d.h. wir wünschen uns ein definiertes Übertragungsverhalten. Dem Eingangssignal sollte zudem möglichst gut und schnell gefolgt werden, d.h. es sollten keine allzu großen Verzögerungen auftreten. Dies wird über das dynamische Verhalten des verwendeten OPs bestimmt. Reale OPs haben eine begrenzte Bandbreite die berücksichtigt werden muss. Am Ausgang sollte ein möglichst kleiner Innenwiderstand vorzufinden sein, sodass wir ein eingeprägtes Ausgangssignal annehmen können, d.h. das Ausgangssignal ist gut weiterverwendbar und beeinflusst nicht die folgende Schaltung.

Elektrometerverstärker#

Der Elektrometerverstärker verstärkt ein gewisses Eingangssignal und besteht aus einem Operationsverstärker mit zwei Widerständen wie in Abb. 87 dargestellt.

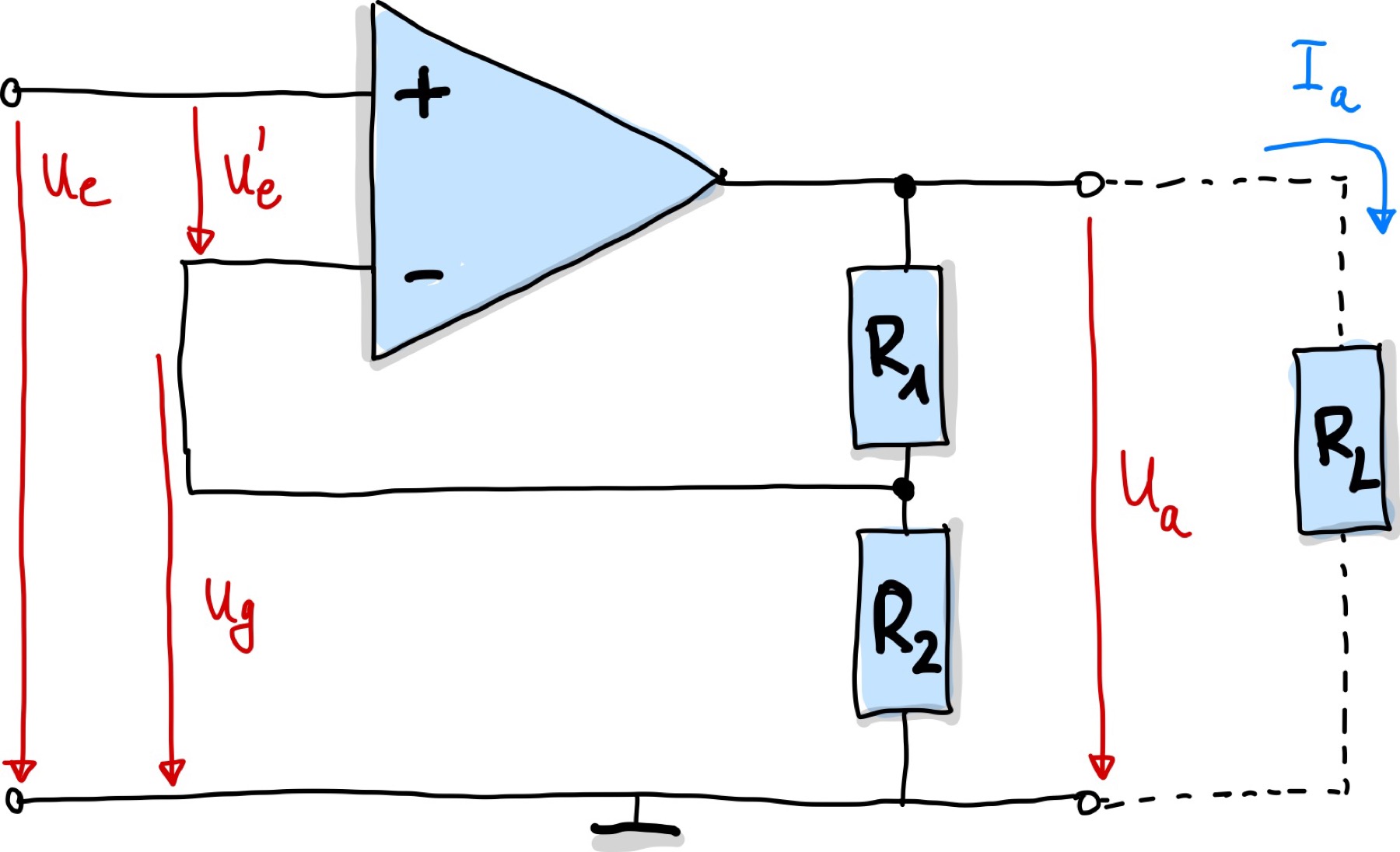
op_electro

Abb. 87 Schematische Darstellung eines Elektrometerverstärkers.#

Folgende Beziehung kann über die Maschenregel hergeleitet werden, wenn der Eingangsschaltkreis betrachtet wird:

\[U_e - \frac{R_2}{R_1+R_2} U_a - U'_e = 0\]

wobei \(U_e\) die Eingangsspannung ist, \(U_a\) die Ausgangsspannung und \(U'_e\) die Spannung, die am Eingang des OPs abfällt. Daraus folgt:

\[U'_e = U_e - \frac{R_2}{R_1+R_2} U_a\]

Für den Ausgangsschaltkreis folgt mittels Maschenregel:

\[k U'_e - I_a R_L - I_a R_i = kU'_e - U_a - U_a \frac{R_i}{R_L} = 0\]

wobei \(k\) der Verstärungsfaktor des OPs ist, die auf die Eingangsspannung \(U'_e\) des OPs wirkt. \(R_L\) der Laserwiderstand und \(I_a\) die Ausgangsstromstärke.

Die beiden Gleichungen werden so kombiniert, dass alle \(U'_e\) eliminiert werden:

\[U_e - U_a \left( \frac{R_1}{R_1+R_2} - \frac{1}{k} - \frac{R_i}{kR_L} \right) = 0\]

und wir können die Gleichung nach der Elektrometer-Verstärkung \(k_E = U_a / U_e\) umformen:

\[k_E = \frac{U_a}{U_e} = \frac{1}{\frac{R_1}{R_1 + R_2} - \frac{1}{k} - \frac{R_i}{kR_L}}\]

\(k_E\) ist hierbei der Verstärkungsfaktor der kompletten Schaltung und \(k\) die Verstärkung des OPs.

Für einen idealen OP (\(k \rightarrow \infty\)) folgt:

\[U_a = \left( 1 + \frac{R_1}{R_2} \right) U_e\]

Impedanzverstärker#

Auch hier gibt es wieder ein Rückkopplung vom Ausgang des OPs an den Eingang.

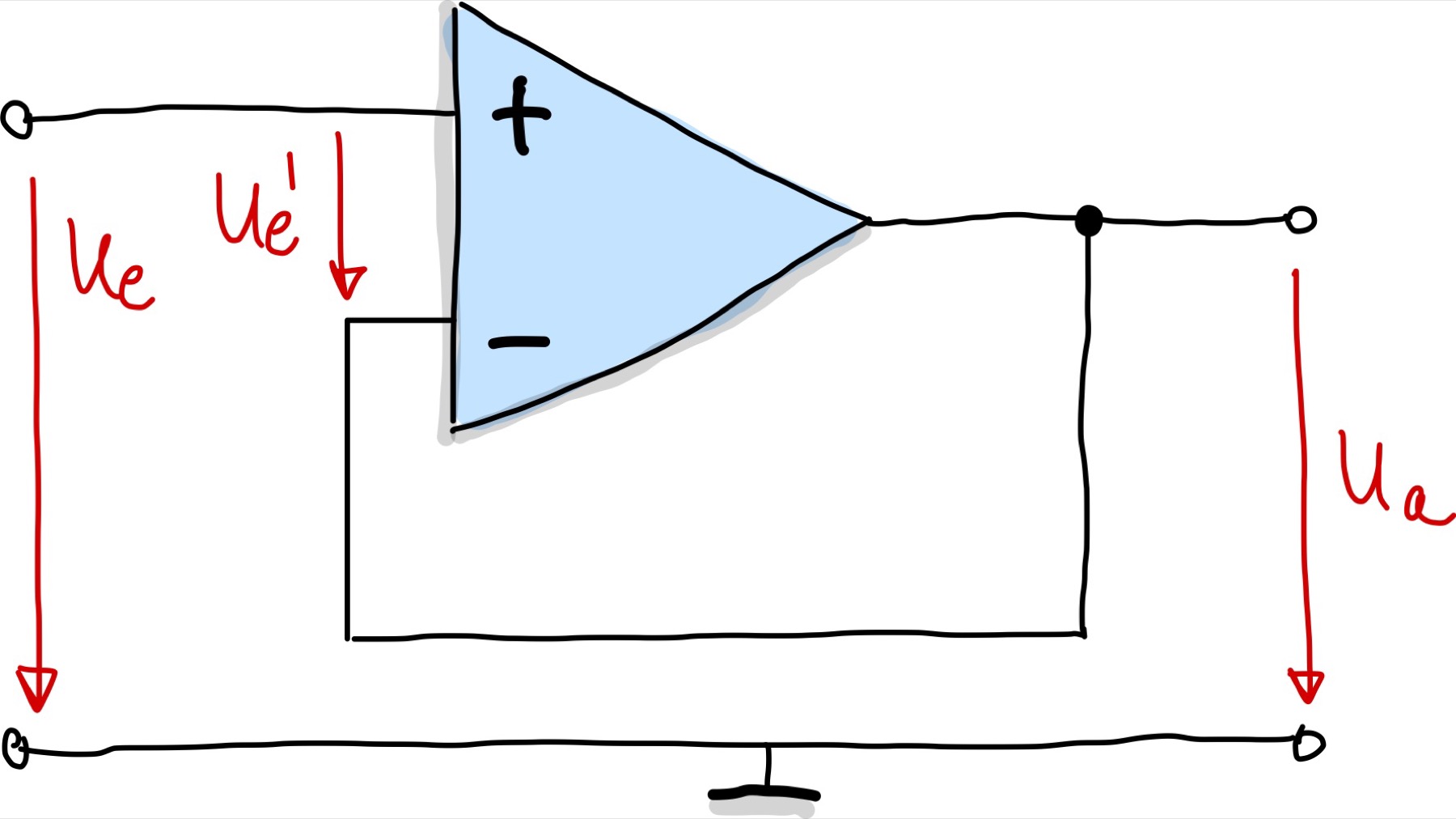
op_impedanz

Abb. 88 Schematische Darstellung eines Impedanzwandlers.#

Für einen idealen OP gilt

\[U'_e = 0\]

Über die Maschenregel folgt:

\[U_e = U_a\]

Dass die Ausgangsspannung dem Eingangssignal bedinglos folgt gilt jedoch nur für bestimmte Grenzfrequenzen der OPs und der Schaltung, da ein OP ein dynamisches Verhalten aufweist. Die maximale Frequenzen, die der OP noch übertragen kann, passen den Verstärkungsfaktor an, bzw. umgekehrt.

Strom-Spannungs-Wandler/Verstärker#

Wir gehen wieder davon aus, dass wir einen idealen Verstärker vorliegen haben, d.h.

\[U'_e = 0\]
op_IU

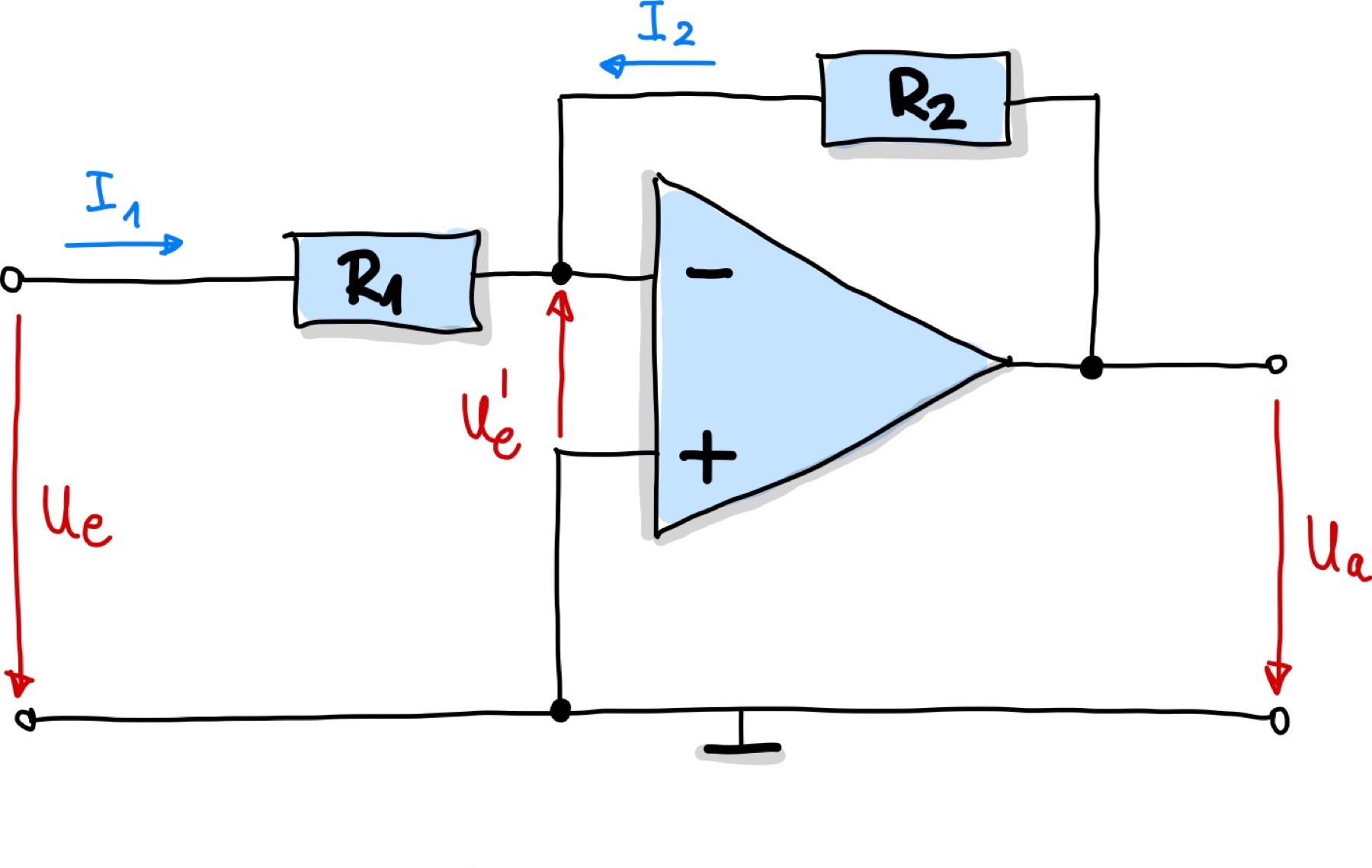
Abb. 89 Schematische Darstellung eines Strom-Spannungs-Verstärkers.#

Diese Spannung treibt den Strom \(I_{1}\) an, wobei durch den OP kein Strom fließt, d.h. der gesamte Strom muss durch \(R_1\) fließen:

\[I_{1} = \frac{U_e}{R_1}\]

Abfließen kann dies durch den Widerstand \(R_2\), d.h. es gilt nach der Knotenregel:

\[I_{2} = -I_{1}\]

Dadurch folgt:

\[I_{1} = \frac{U_e}{R_1} = -I_{2} = -\frac{U_a}{R_2}\]

Dies kann so umgeformt werden, dass sich der Verstärkungsfaktor \(k = U_a/U_e\) der Schaltung ergibt:

\[k = -\frac{R_2}{R_1}\]

Es handelt sich also um eine Verstärkerschaltung für Spannungen, bzw. um einen Stromwandler.

Weitere Beispiele und Verstärkungsfaktoren sind in Abb. 90 dargestellt.

Weitere Beispiele#

ops

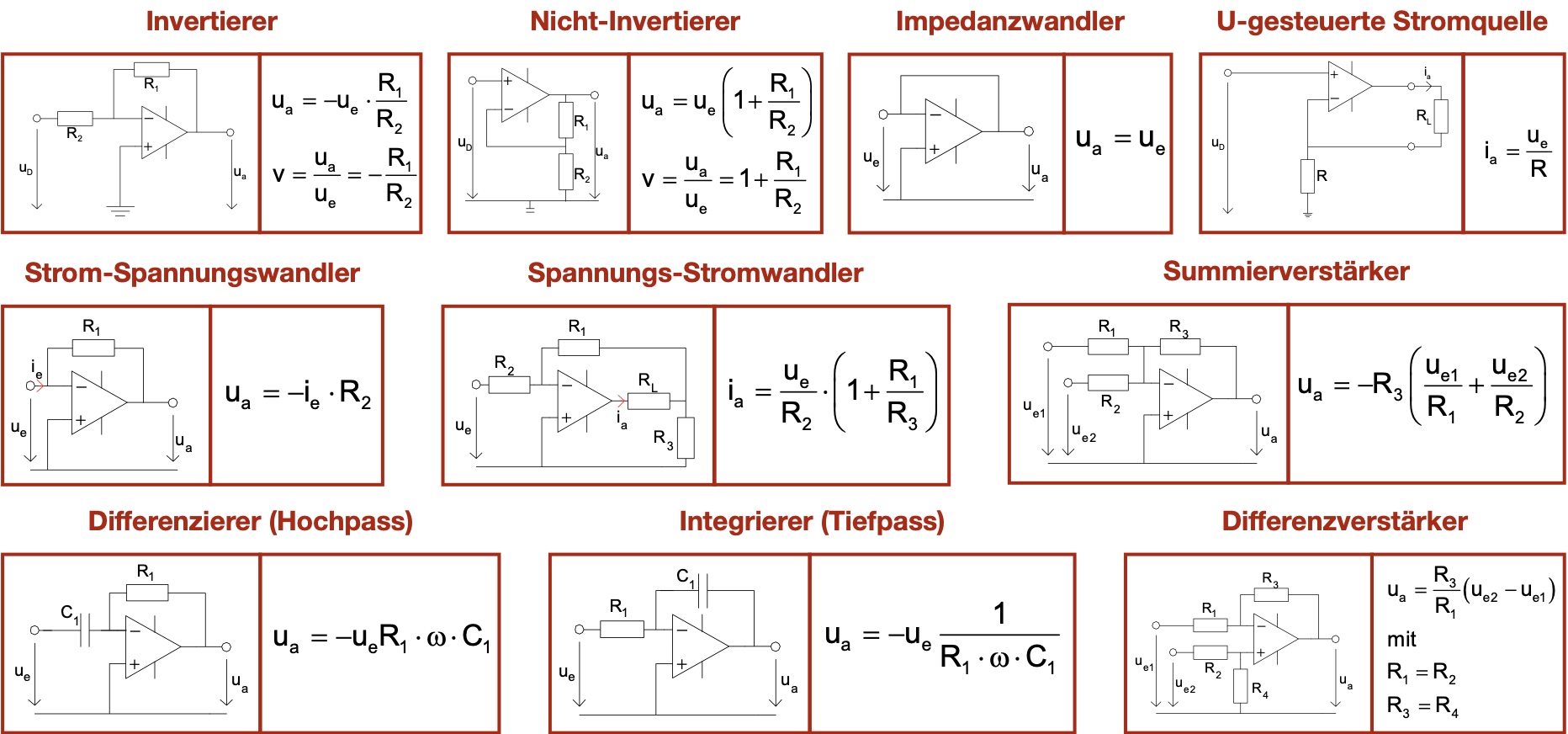
Abb. 90 Verschiedene Operationsverstärker-Schaltungen inklusive Verstärkungsfaktor.#