Klimadaten auswerten#
In diesem Jupyter Notebook werden wir die Klimadaten der NASA aus und lernen die wichtigsten Python hierfür kennen, die Sie auch für das Messtechnik-Praktikum benötigen um Ihre Versuche auszuwerten.
Zunächst werden die für dieses Jupyter Notebook benötigten Libraries geladen:
#Benötigte Libraries:
import numpy as np
import pandas as pd # Dataframes
import matplotlib.pyplot as plt
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
import seaborn as sns
import time
import warnings
warnings.filterwarnings('ignore')
# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
plt.rcParams['font.size'] = 10; # Schriftgröße
.csv-Datei als DataFrame einlesen#
Im Folgenden Nutzen wir globale Klimadaten, die auf der Webseite der NASA zu finden sind: https://data.giss.nasa.gov/gistemp/. Hierbei handelt es sich um Temperaturdaten, die Anomalien gegenüber dem Mittelwert in den Jahren 1951-1980 aufweisen.
Es werden Daten von Dateien (online oder offline) eingelesen mit der Python Bilbiothek pandas. Die Daten werden in sogenannten DataFrames hier mit dem Namen global_mean abgespeichert.
link = "https://data.giss.nasa.gov/gistemp/graphs_v4/graph_data/Global_Mean_Estimates_based_on_Land_and_Ocean_Data/graph.csv"
#link = 'data/graph.csv'
global_mean = pd.read_csv(link, header = 1) #DataFrame erstellen
global_mean
| Year | No_Smoothing | Lowess(5) | |
|---|---|---|---|
| 0 | 1880 | -0.17 | -0.10 |
| 1 | 1881 | -0.09 | -0.13 |
| 2 | 1882 | -0.11 | -0.17 |
| 3 | 1883 | -0.17 | -0.20 |
| 4 | 1884 | -0.28 | -0.24 |
| ... | ... | ... | ... |
| 140 | 2020 | 1.01 | 0.97 |
| 141 | 2021 | 0.85 | 1.02 |
| 142 | 2022 | 0.89 | 1.08 |
| 143 | 2023 | 1.17 | 1.13 |
| 144 | 2024 | 1.28 | 1.19 |
145 rows × 3 columns
Wir geben das DataFrame aus um uns die Messdaten einmal anzusehen:
global_mean.head(10) # Ausgabe der ersten 5 Spalten
#global_mean.tail(5) # Ausgabe der letzten 5 Spalten
#global_mean # Ausgabe des DataFrames
| Year | No_Smoothing | Lowess(5) | |
|---|---|---|---|
| 0 | 1880 | -0.17 | -0.10 |
| 1 | 1881 | -0.09 | -0.13 |
| 2 | 1882 | -0.11 | -0.17 |
| 3 | 1883 | -0.17 | -0.20 |
| 4 | 1884 | -0.28 | -0.24 |
| 5 | 1885 | -0.33 | -0.26 |
| 6 | 1886 | -0.31 | -0.27 |
| 7 | 1887 | -0.36 | -0.27 |
| 8 | 1888 | -0.18 | -0.27 |
| 9 | 1889 | -0.11 | -0.26 |
In der ersten Spalte befinden sich lediglich die Indizes der Messungen. Die zweite Spalte beinhaltet das Jahr und die dritte Spalte zeigt den gemessenen globalen Temperaturunterschied im Vergleich zur gemittelten Temeratur der Jahre 1951-1980. Die letzte Spalte zeigt die gleichen Messwerte, jedoch gefiltert.
Einzelne Spalten kann man sich anzeigen lassen, indem den Spaltel-Namen des zugehörigen DataFrames nutzt:
global_mean['Year']
0 1880
1 1881
2 1882
3 1883
4 1884
...
140 2020
141 2021
142 2022
143 2023
144 2024
Name: Year, Length: 145, dtype: int64
Statistische Größen#
Die Bibliothek pandas ist sehr umfangreich und wird viel zur Datenverarbeitung genutzt. Im folgenden dazu einige Beispiele:
Statistische Größen: Mittelwert, Standardabweichung, Min, Max#
Für jede Spalte lassen sich statistische Größen wie z.B. die Anzahl der Einträge pro Spalte, deren Mittelwert, Standardabweichung, Minimal- und Maximalwert bestimmen:
print(global_mean.describe())
#print(global_mean['No_Smoothing'].describe())
#print(global_mean['Lowess(5)'].describe())
std_year = global_mean['Year'].std()
print(mean_year)
Year No_Smoothing Lowess(5)
count 145.000000 145.000000 145.000000
mean 1952.000000 0.072966 0.073931
std 42.001984 0.392561 0.384890
min 1880.000000 -0.490000 -0.420000
25% 1916.000000 -0.200000 -0.230000
50% 1952.000000 -0.030000 -0.040000
75% 1988.000000 0.310000 0.310000
max 2024.000000 1.280000 1.190000
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[5], line 6
3 #print(global_mean['No_Smoothing'].describe())
4 #print(global_mean['Lowess(5)'].describe())
5 std_year = global_mean['Year'].std()
----> 6 print(mean_year)
NameError: name 'mean_year' is not defined
Die mittlere Jahresmitteltemperaturabweichung im Vergleich zu 1951-1980 beträgt in diesem Fall 0,07 Grad Celsius. Der Trend ist also positiv und im Mittel müssen wir mit einer Erwärmung rechnen, auch wenn einige Jahre negative Jahresmitteltemperaturabweichungen aufzeigen.
Kälteste Jahre#
Die folgenden Jahre weisen die niedrigsten Werte der Temperatur-Anomalie auf.
Sie repräsentieren die kältesten Phasen in der betrachteten Zeitreihe.
Als erstes wenden wir einen Filter auf die Jahre mit negativer Temperatur-Anomalie an:
cold_years = global_mean[global_mean["No_Smoothing"] < 0] # Filter auf Jahre mit negativer Temperatur-Anomalie
Mit .sort_values("Spaltenname") können wir die Tabelle nach dem definierten Spaltennamen sortieren (standardmäßig in ansteigender Reihenfolge):
# Sortieren nach kältesten Jahren (kleinste Werte zuerst)
cold_years_sorted = cold_years.sort_values(by="No_Smoothing")
# Ausgabe der Top 10 kältesten Jahre
print(cold_years_sorted.head(10))
Year No_Smoothing Lowess(5)
29 1909 -0.49 -0.42
24 1904 -0.48 -0.32
37 1917 -0.47 -0.31
31 1911 -0.45 -0.40
30 1910 -0.44 -0.42
28 1908 -0.44 -0.40
27 1907 -0.40 -0.38
32 1912 -0.38 -0.36
23 1903 -0.38 -0.29
49 1929 -0.37 -0.20
Und wenn man nur die Jahreszahlen und Werte angezeigt bekommen möchte:
cold_years_sorted[["Year", "No_Smoothing"]].head(10)
| Year | No_Smoothing | |
|---|---|---|
| 29 | 1909 | -0.49 |
| 24 | 1904 | -0.48 |
| 37 | 1917 | -0.47 |
| 31 | 1911 | -0.45 |
| 30 | 1910 | -0.44 |
| 28 | 1908 | -0.44 |
| 27 | 1907 | -0.40 |
| 32 | 1912 | -0.38 |
| 23 | 1903 | -0.38 |
| 49 | 1929 | -0.37 |
Wärmste Jahre#
Die folgenden Jahre weisen die höchsten Werte der Temperatur-Anomalie auf.
Sie repräsentieren die wärmsten Phasen in der betrachteten Zeitreihe.
# Filter auf Jahre mit positiver Temperatur-Anomalie
warm_years = global_mean[global_mean["No_Smoothing"] > 0]
# Sortieren nach wärmsten Jahren (größte Werte zuerst)
warm_years_sorted = warm_years.sort_values(by="No_Smoothing", ascending=False)
# Ausgabe der Top 10 wärmsten Jahre
print(warm_years_sorted.head(10))
Year No_Smoothing Lowess(5)
144 2024 1.28 1.19
143 2023 1.17 1.13
140 2020 1.01 0.97
136 2016 1.01 0.87
139 2019 0.98 0.94
137 2017 0.92 0.91
135 2015 0.90 0.83
142 2022 0.89 1.08
141 2021 0.85 1.02
138 2018 0.85 0.93
Wärmstes Jahr#
Wenn wir wissen wollen, wann diese maximale Temperaturdifferenz auftrat, kann auch der zugehörige Index dieses Events gespeichert werden:
index_max = global_mean["No_Smoothing"].idxmax()
print(index_max)
144
Diesen Index können wir nun benutzen, um mittels .loc die entsprechenden Einträge zu diesem Index auszugeben:
global_mean.loc[index_max]
Year 2024.00
No_Smoothing 1.28
Lowess(5) 1.19
Name: 144, dtype: float64
Daten plotten und Diagramm sichern mit ‘matplotlib’#
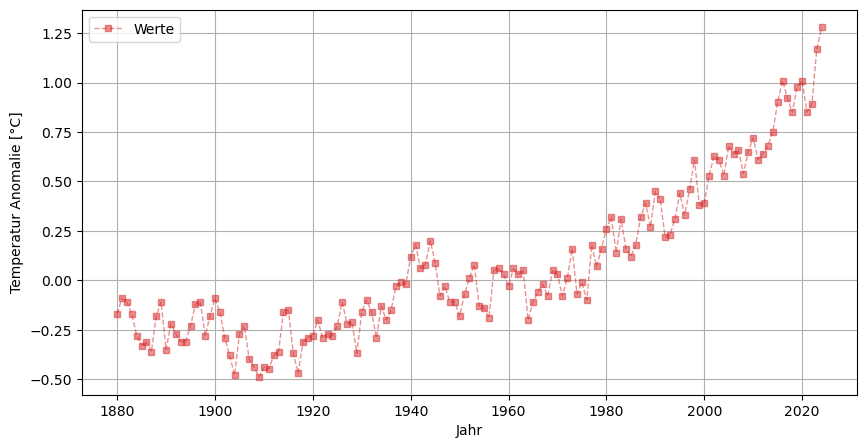
Als Beispiel für eine gelungene grafische Darstellung wollen wir die beiden Spalten, No_Smoothing and Lowess(5) gegenüber der Zeitachse Year plotten. Hierfür benützen wir die Python Library matplotlib. Einmal geplottet kann das zuletzt angezeigte Diagramm in verschiedenen Formaten mit plt.savefig('klima_plot1.png') abgespeichert werden. Wenn nicht anders angegeben, wird die Datei im gleichen Ordner angelegt.
import matplotlib.pyplot as plt
#plt.style.use('default')
plt.figure(figsize=(10,5))
plt.rcParams['font.size'] = 10; # Schriftgröße
plt.plot(global_mean["Year"],global_mean["No_Smoothing"], ls="--", lw=1, marker="s", ms=5, color="tab:red", alpha=0.5, label="Werte");
#plt.plot(global_mean["Year"],global_mean["Lowess(5)"], lw=4, color="tab:blue", label="Glättung (NASA)");
plt.xlabel('Jahr')
plt.ylabel("Temperatur Anomalie [°C]")
plt.legend()
plt.grid()
plt.savefig('klima_plot1.png')
plt.savefig('klima_plot1.pdf')
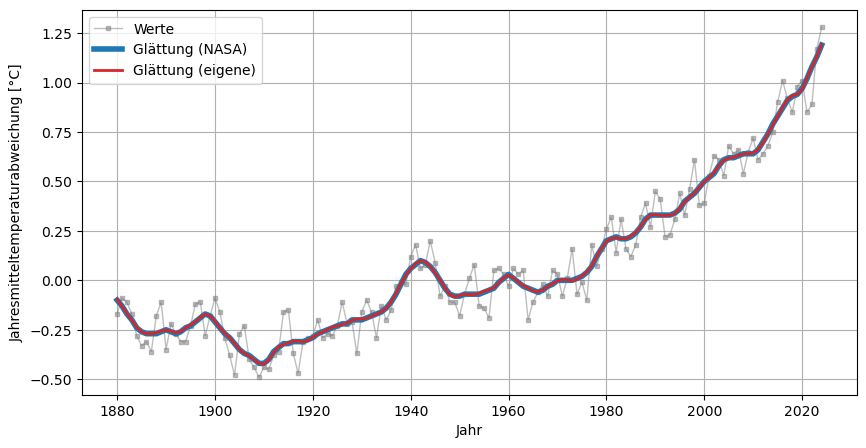
Daten glätten#
Die von der NASA verwendete Glättung ist die LOcally WEighted Scatter-plot Smoother (LOWESS). Dabei wird in einem lokal zu definierenden Bereich eine lineare Regression durchgeführt. Eine genauere Erklärung zur Methode findet ihr auf Youtube.
Es gibt natürlich viele Methoden und Filter, um Daten zu glätten. Wir wollen nun versuchen, die Methode der NASA zu rekonstruieren. Hierfür benutzen wir die Python Library statsmodels und erstellen eine weitere Spalte Lowess(own) in unserem DataFrame global_mean. In diese Spalte schreiben wir die geglätteten Werte von den Rohdaten global_mean["No_Smoothing"] indem wir die Funktion lowess aufrufen. Details zu Nutzung der Funktion findet ihr https://www.statsmodels.org:
an erster Stelle in der Funktion werden die Y-Werte eingegeben, hier
global_mean["No_Smoothing"]an zweiter Stelle in der Funktion werden die X-Werte eingegeben, hier
global_mean["Year"]die Option
fracist eine Zahl zwischen 0 und 1. Dies ist der Anteil der Daten, der bei der Schätzung der einzelnen y-Werte verwendet wird.Ausgegeben wird zweidimensionalas Array. Die erste Spalte enthält die sortierten x-Werte und die zweite Spalte die zugehörigen geschätzten y-Werte. Um die zweite Spalte in den DataFrame zu speichern, wählen wir diese mit
[:,1]aus.
from statsmodels.nonparametric.smoothers_lowess import lowess
global_mean["Lowess(eigene)"] = lowess(global_mean["No_Smoothing"],global_mean["Year"], frac=1/14)[:,1]
global_mean
| Year | No_Smoothing | Lowess(5) | Lowess(eigene) | |
|---|---|---|---|---|
| 0 | 1880 | -0.17 | -0.10 | -0.096166 |
| 1 | 1881 | -0.09 | -0.13 | -0.131758 |
| 2 | 1882 | -0.11 | -0.17 | -0.167628 |
| 3 | 1883 | -0.17 | -0.20 | -0.202299 |
| 4 | 1884 | -0.28 | -0.24 | -0.236649 |
| ... | ... | ... | ... | ... |
| 140 | 2020 | 1.01 | 0.97 | 0.965670 |
| 141 | 2021 | 0.85 | 1.02 | 1.023666 |
| 142 | 2022 | 0.89 | 1.08 | 1.078238 |
| 143 | 2023 | 1.17 | 1.13 | 1.133268 |
| 144 | 2024 | 1.28 | 1.19 | 1.191802 |
145 rows × 4 columns
plt.figure(figsize=(10,5))
plt.rcParams['font.size'] = 10;
plt.plot(global_mean["Year"],global_mean["No_Smoothing"], ls="-", lw=1, marker="s", ms=3, color="tab:gray", alpha=0.5, label="Werte");
plt.plot(global_mean["Year"],global_mean["Lowess(5)"], lw=4, color="tab:blue", label="Glättung (NASA)");
plt.plot(global_mean["Year"],global_mean["Lowess(eigene)"], lw=2,ls='-' , color="tab:red", label="Glättung (eigene)");
plt.xlabel('Jahr')
plt.ylabel("Jahresmitteltemperaturabweichung [°C]")
plt.legend();
plt.grid();
plt.savefig('klima_plot2.png')
plt.savefig('klima_plot2.pdf')
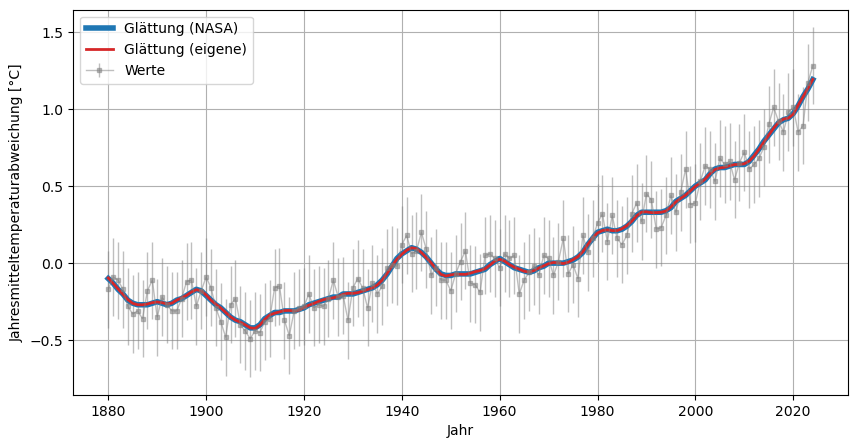
Messunsicherheiten als Fehlerbalken hinzufügen#
Bei diesem Datenset stehen uns leider keine Messunsicherheiten zur Verfügung. Um Sie jedoch als Fehlerbalken miteinzubeziehen, wollen wir im Folgenden annehmen, dass der Temperaturunterschied auf 0.25K genau messen werden konnte und fügen die unserem Datensatz hinzu:
global_mean["uncertainty"] = 0.25
print(global_mean)
Year No_Smoothing Lowess(5) Lowess(eigene) uncertainty
0 1880 -0.17 -0.10 -0.096166 0.25
1 1881 -0.09 -0.13 -0.131758 0.25
2 1882 -0.11 -0.17 -0.167628 0.25
3 1883 -0.17 -0.20 -0.202299 0.25
4 1884 -0.28 -0.24 -0.236649 0.25
.. ... ... ... ... ...
140 2020 1.01 0.97 0.965670 0.25
141 2021 0.85 1.02 1.023666 0.25
142 2022 0.89 1.08 1.078238 0.25
143 2023 1.17 1.13 1.133268 0.25
144 2024 1.28 1.19 1.191802 0.25
[145 rows x 5 columns]
Grafisch darstellen tun wir Messunsicherheiten mittels Fehlerbalken und der Matplotlib-Funktion plt.errorbar.
plt.figure(figsize=(10,5))
plt.rcParams['font.size'] = 10;
plt.errorbar(global_mean["Year"],global_mean["No_Smoothing"], yerr=global_mean["uncertainty"], ls="-", lw=1, marker="s", ms=3, color="tab:gray", alpha=0.5, label="Werte");
plt.plot(global_mean["Year"],global_mean["Lowess(5)"], lw=4, color="tab:blue", label="Glättung (NASA)");
plt.plot(global_mean["Year"],global_mean["Lowess(eigene)"], lw=2,ls='-' , color="tab:red", label="Glättung (eigene)");
plt.xlabel('Jahr')
plt.ylabel("Jahresmitteltemperaturabweichung [°C]")
plt.legend();
plt.grid();
plt.savefig('klima_plot3.png')
plt.savefig('klima_plot3.pdf')
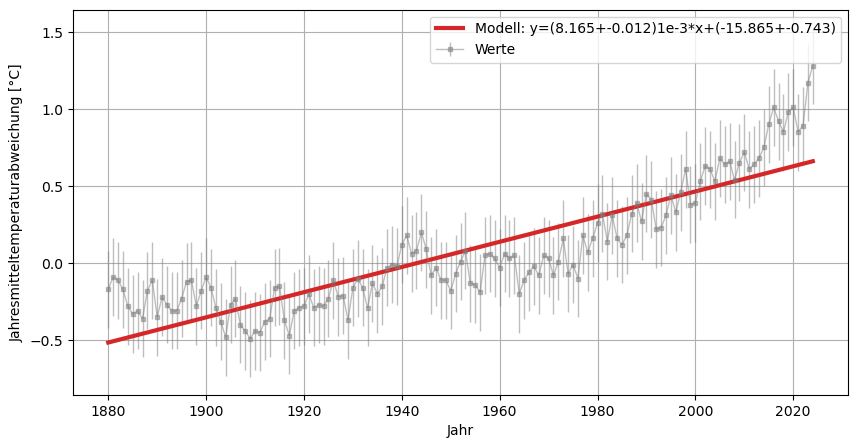
Modellfunktionen an Daten anpassen#
Lineare Regression#
Mittels linearer Regression kann der Temperaturanstieg aus den Daten berechnet werden. Hierfür wird die Python Library numpy benutzt und die Funktion polyfit aufgerufen und in als model gespeichert. Diese Funktion benutzt die Least-Square Methode für polynomische Modelle. Weitere Informationen zu der Funktion findet ihr hier. Mit der Option cov=True wird die Kovarianz-Matrix berechnet, welche die Unsicherheiten für die Fit-Parameter beinhaltet.
x=global_mean["Year"]
y=global_mean["No_Smoothing"]
y_err = global_mean["uncertainty"]
model_lin1 = np.polyfit(x, y, deg=1, w=1/y_err, cov=True) # 1. Wert = Anstieg , 2. Wert = Schnittpunkt mit y-Achse
y_model_1 = model_lin1[0][0]*x+model_lin1[0][1] # Modell einer linearen Regression
plt.figure(figsize=(10,5))
plt.rcParams['font.size'] = 10;
plt.ylabel("Jahresmitteltemperaturabweichung [°C]")
plt.xlabel("Jahr")
plt.errorbar(global_mean["Year"],global_mean["No_Smoothing"], yerr=global_mean["uncertainty"], ls="-", lw=1, marker="s", ms=3, color="tab:gray", alpha=0.5, label="Werte");
plt.plot(x,y_model_1, ls="-", lw=3, color="tab:red", label=f"Modell: y=({model_lin1[0][0]*1000:.3f}+-{np.sqrt(model_lin1[1][0][0]*1000):.3f})1e-3*x+({model_lin1[0][1]:.3f}+-{np.sqrt(model_lin1[1][1][1]):.3f})");
plt.legend();
plt.grid();
plt.savefig('klima_plot4.png')
plt.savefig('klima_plot4.pdf')
Das Model beinhaltet zwei Matrizen:
model_lin1[1]
array([[ 1.44641636e-07, -2.82340474e-04],
[-2.82340474e-04, 5.51382018e-01]])
Im ersten Array stehen die Fit-Parameter der linearen Ausgleichsgeraden entsprechend der obigen Deklaration: y_model_1 = model_lin1[0][0]*x+model_lin1[0][1].
Im zweiten Array, hier eine 2x2 Matrix, sind die Unsicherheiten in Form von der Kovarianz-Matrix dargestellt.
Der Temperaturanstieg kann entsprechend ausgegeben werden:
print(f"Temperaturanstieg pro Jahr (von 1981 bis 2020): {model_lin1[0][0]:.3f}°C/Jahr")
print(f"Temperaturanstieg seit Beginn der Messung: {(y_model_1.iloc[-1]-y_model_1.iloc[0]):.3f}°C")
Temperaturanstieg pro Jahr (von 1981 bis 2020): 0.008°C/Jahr
Temperaturanstieg seit Beginn der Messung: 1.176°C
Warnung
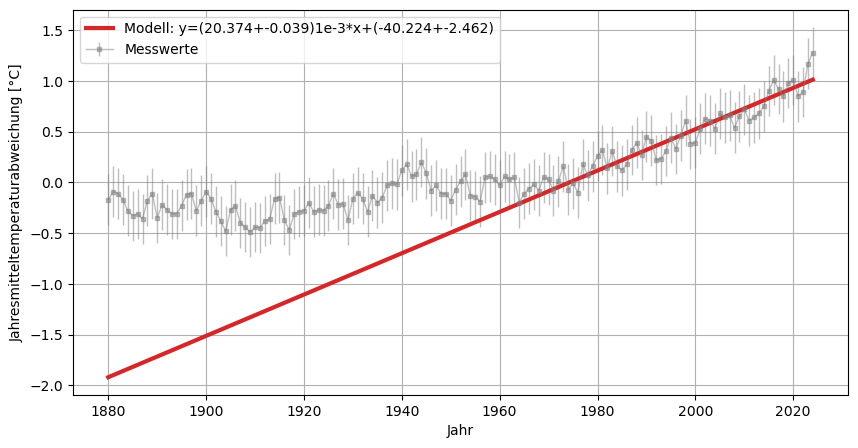
Die lineare Regression bezieht hier den ganzen Zeitraum mit ein! Im folgenden betrachten wir für den Temperaturgradienten nur die Daten von 1980 bis 2020!
x_1980=global_mean.loc[global_mean["Year"] >= 1980,"Year"]
y_1980=global_mean.loc[global_mean["Year"] >= 1980,"No_Smoothing"]
y_err = global_mean.loc[global_mean["Year"] >= 1980,"uncertainty"]
model_lin2 = np.polyfit(x_1980, y_1980, deg=1, w=1/y_err, cov=True) # 1. Wert = Anstieg , 2. Wert = Schnittpunkt mit y-Achse
y_model_2 = model_lin2[0][0]*x+model_lin2[0][1] # Modell einer linearen Regression
plt.figure(figsize=(10,5))
plt.rcParams['font.size'] = 10;
plt.ylabel("Jahresmitteltemperaturabweichung [°C]")
plt.xlabel("Jahr")
plt.errorbar(global_mean["Year"],global_mean["No_Smoothing"], yerr=global_mean["uncertainty"], ls="-", lw=1, marker="s", ms=3, color="tab:gray", alpha=0.5, label="Messwerte");
plt.plot(x,y_model_2, ls="-", lw=3, color="tab:red", label=f"Modell: y=({model_lin2[0][0]*1000:.3f}+-{np.sqrt(model_lin2[1][0][0]*1000):.3f})1e-3*x+({model_lin2[0][1]:.3f}+-{np.sqrt(model_lin2[1][1][1]):.3f})");
plt.legend();
plt.grid();
plt.savefig('klima_plot5.png')
plt.savefig('klima_plot5.pdf')
# Temperaturanstieg pro Jahr:
print(f"Temperaturanstieg pro Jahr (von 1980 bis 2020): {model_lin2[0][0]:.3f}°C/Jahr")
# Vorhersage für Jahr 2050
x_val = 2050
y_pred = np.polyval(model_lin2[0], x_val)
print("Vorhersage für 2050:", y_pred)
Temperaturanstieg pro Jahr (von 1980 bis 2020): 0.020°C/Jahr
Vorhersage für 2050: 1.5430715854193977
Beliebige Funktion fitten#
Mit der Polyfit Funktion können in erster Linie Polynome gefittet werden.
Für beliebige Modellierung, wie z.B. quadratische oder Exponential-Funktionen, werden die Funktionen in aller Regel selber definiert. Hierfür eignet sich die scipy-Funktion curve_fit.
from scipy.optimize import curve_fit
Als erstes wird die Funktion deklariert:
def quadratic_fit(x, a, b, c):
return a*x**2 + b*x + c
Die Funktion wird anschließend an die Daten angepasst:
# Nutze alle Daten über die gesamte Zeit, nicht gefiltert:
x=global_mean["Year"]
y=global_mean["No_Smoothing"]
y_err = global_mean["uncertainty"]
model_quadr = curve_fit(quadratic_fit, x, y)
y_model_quadr = model_quadr[0][0]*x**2 + model_quadr[0][1]*x + model_quadr[0][2]
print(model_quadr)
(array([ 9.43408527e-05, -3.60141597e-01, 3.43436749e+02]), array([[ 4.12615232e-11, -1.61084987e-07, 1.57146658e-04],
[-1.61084987e-07, 6.28933616e-04, -6.13613427e-01],
[ 1.57146658e-04, -6.13613427e-01, 5.98721651e+02]]))
Man sieht, je komplexer die Modellfunktion ist, desto schwieriger ist es die Matrizen zu lesen. Daher können die Modelparameter und die Kovarianzmatrix auch separat voneinander gespeichert werden:
popt, pcov = curve_fit(quadratic_fit, x, y)
print('Modellparameter:', popt)
print('Mit der Kovarianz-Matrix und entsprechende Unsicherheiten:', pcov)
print(model_quadr[0][1])
Modellparameter: [ 9.43408527e-05 -3.60141597e-01 3.43436749e+02]
Mit der Kovarianz-Matrix und entsprechende Unsicherheiten: [[ 4.12615232e-11 -1.61084987e-07 1.57146658e-04]
[-1.61084987e-07 6.28933616e-04 -6.13613427e-01]
[ 1.57146658e-04 -6.13613427e-01 5.98721651e+02]]
-0.3601415966534972
plt.figure(figsize=(10,5))
plt.rcParams['font.size'] = 10;
plt.ylabel("Jahresmitteltemperaturabweichung [°C]")
plt.xlabel("Jahr")
plt.errorbar(global_mean["Year"],global_mean["No_Smoothing"], yerr=global_mean["uncertainty"], ls="-", lw=1, marker="s", ms=3, color="tab:gray", alpha=0.5, label="Messwerte");
plt.plot(x,quadratic_fit(x,*popt), ls="-", lw=3, color="tab:red", label=f"Modell: y=({model_quadr[0][0]*1000:.3f}+-{np.sqrt(model_quadr[1][0][0]*1000):.3f})1e-3*x^2+({model_quadr[0][1]:.3f}+-{np.sqrt(model_quadr[1][1][1]):.3f})*x + ({model_quadr[0][2]:.3f}+-{np.sqrt(model_quadr[1][2][2]):.3f})");
plt.legend();
plt.grid();
plt.savefig('klima_plot6.png')
plt.savefig('klima_plot6.pdf')
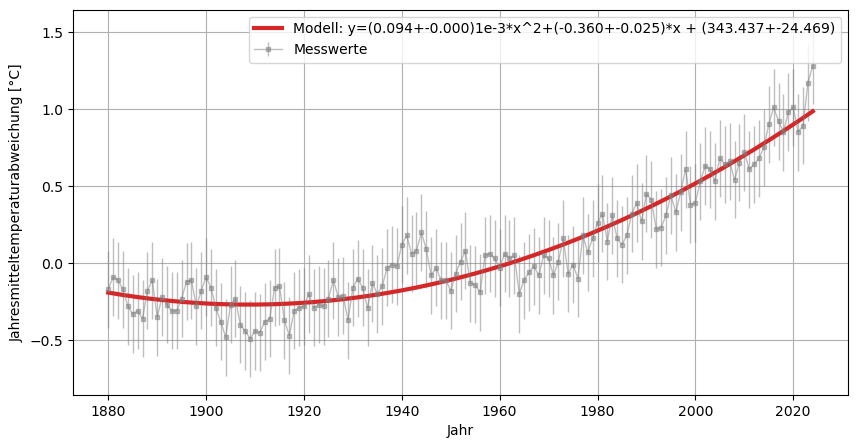
Für ein exponentielles Modell passen wir die x-Achse ein wenig an und gehen dann wie schon oben vor:
plt.figure(figsize=(10,5))
plt.rcParams['font.size'] = 10;
# Daten normieren
xdata = (global_mean["Year"].values - 1880) / 100 # auf Jahrhunderte
ydata = global_mean["No_Smoothing"].values
# Modell
def exp_model(x, a, b, c):
return a * np.exp(b * x) + c
# Startwerte + Bounds
p0 = (1.0, 0.0001, -0.5)
bounds = ([-1, 0, -2], [5, 4.0, 2])
# Fit
popt_exp, pcov_exp = curve_fit(exp_model, xdata, ydata, p0=p0, bounds=bounds)
a, b, c = popt_exp
print(f"a = {a:.4f}, b = {b:.6f}, c = {c:.4f}")
# Vorhersage
xline = np.linspace(min(xdata), max(xdata), 200)
yfit = exp_model(xline, *popt_exp)
plt.errorbar(global_mean["Year"],global_mean["No_Smoothing"], yerr=global_mean["uncertainty"], ls="-", lw=1, marker="s", ms=3, color="tab:gray", alpha=0.5, label="Messwerte");
#plt.scatter(xdata*100+1880, ydata, s=10, color="tab:gray", label="Klimadaten")
plt.plot(xline*100+1880, yfit, color="tab:red", lw = 3, label="Exponential-Fit f(x) = " f"{a:.2f} * exp ({b:.4f}*x) + {c:.2f}")
plt.xlabel("Jahr")
plt.ylabel("Jahresmitteltemperaturabweichung [°C]")
plt.legend()
plt.grid();
plt.savefig('klima_plot8.png')
plt.savefig('klima_plot8.pdf')
print("Vorhersage für das Jahr x = 2050:", exp_model((2050-1880)/100, *popt_exp))
print("")
a = 0.0422, b = 2.450713, c = -0.3252
Vorhersage für das Jahr x = 2050: 2.3961871141807887
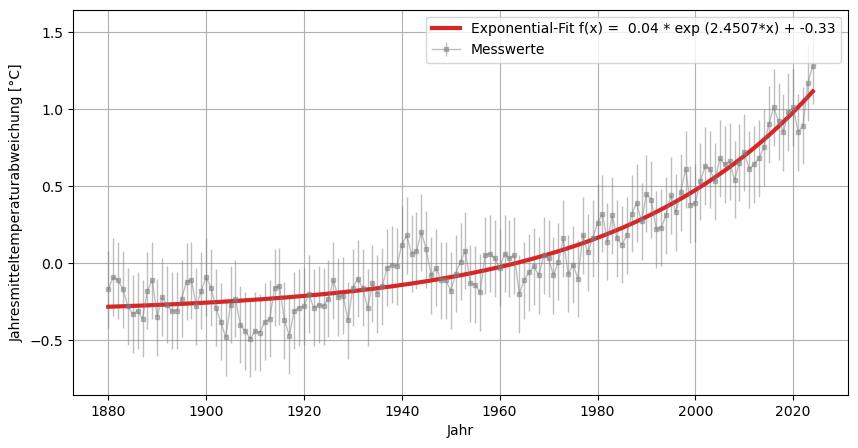
Vorhersage für das Jahr 2050#
# Vorhersage für Jahr 2050
x_val = 2050
y_pred_lin1 = np.polyval(model_lin1[0], x_val)
print("Lineares Modell 1 (1880-2025):\t", y_pred_lin1)
y_pred_lin2 = np.polyval(model_lin2[0], x_val)
print("Lineares Modell 2 (1981-2025):\t", y_pred_lin2)
y_pred_quadr = np.polyval(model_quadr[0], x_val)
print("Quadratisches Modell:\t\t", y_pred_quadr)
# Exponentielles Modell (x normieren!)
x_val_exp = (x_val - 1880) / 100
y_pred_exp = exp_model(x_val_exp, *popt_exp)
print("Exponentielles Modell:\t\t", y_pred_exp)
Lineares Modell 1 (1880-2025): 0.8731445441662782
Lineares Modell 2 (1981-2025): 1.5430715854193977
Quadratisches Modell: 1.6139089222256189
Exponentielles Modell: 2.3961871141807887
Wie gut passen die Modelle?#
Die Güte eines Modells oder einer Fit-Funktion lässt sich auf verschiedene Weise beurteilen. Typische Kennwerte sind die Residuen, die Residuensumme bzw. deren Standardfehler sowie der sogenannte \(\chi^2\)-Wert.
Für die Berechnung des \(\chi^2\)-Werts werden jedoch die geschätzten Unsicherheiten der Messwerte benötigt – diese sind in der Praxis nicht immer bekannt.
In der Anwendung testet man daher oft mehrere Modelle, passt sie an die Messdaten an und vergleicht anschließend die ausgegebenen Parameter und Gütemaße miteinander. Auf diese Weise lässt sich erkennen, welches Modell die vorhandenen Daten am besten beschreibt.
Wichtig ist jedoch:
Auch wenn ein Modell besser passt als andere, bedeutet das nicht automatisch, dass es das optimale Modell ist.
Ebenso wenig ist damit geklärt, ob das Modell tatsächlich das richtige ist, d. h. die zugrunde liegenden physikalischen Zusammenhänge korrekt abbildet.
Im folgenden Code werden verschiedene Kenngrößen berechnet, um die Anpassung (Fit-Güte) mehrerer Modelle an Messdaten zu beurteilen.
Die Residuen sind die Abweichungen zwischen den gemessenen Werten \(y_i\) und den durch das Modell vorhergesagten Werten \(f(x_i)\):
Die Residuensumme (Sum of Squared Residuals, SSR) misst die Gesamtabweichung des Modells von den Daten:
Der Standardfehler der Residuen oder Root Mean Square Error (RMSE) normiert die Abweichung auf die Freiheitsgrade:
mit den Freiheitsgraden \(\nu = N - k\), wobei \(k\) die Anzahl der Modellparameter ist. Die Freiheitsgrade geben an, wie viel unabhängige Information nach der Modellanpassung übrigbleibt.
Der Chi-Quadrat-Wert berücksichtigt zusätzlich die Messunsicherheiten \(s_i\) der Daten:
Durch Normierung auf die Freiheitsgrade erhält man den reduzierten Chi-Quadrat-Wert:
Das Bestimmtheitsmaß \(R^2\) gibt an, wie viel der Gesamtvarianz der Daten durch das Modell erklärt wird:
Das korrigierte Bestimmtheitsmaß \(R^2_\text{korr}\) berücksichtigt zusätzlich die Anzahl der Parameter \(k\) und bestraft übermäßig komplexe Modelle:
from sklearn.metrics import r2_score
# --- Residuen (Lineare und Quadratische Modelle) ---
residuals_lin1 = y - (model_lin1[0][0]*x + model_lin1[0][1])
residuals_lin2 = y_1980 - (model_lin2[0][0]*x_1980 + model_lin2[0][1])
residuals_quadr = y - quadratic_fit(x,*popt)
residuals_exp = ydata - exp_model(xdata, *popt_exp)
# --- Freiheitsgrade ---
dof_lin1 = len(x) - len(model_lin1[0])
dof_lin2 = len(x_1980) - len(model_lin2[0])
dof_quadr = len(x) - len(model_quadr[0])
dof_exp = len(xdata) - len(popt_exp)
# --- SSR ---
ssr_lin1 = np.sum(residuals_lin1**2)
ssr_lin2 = np.sum(residuals_lin2**2)
ssr_quadr = np.sum(residuals_quadr**2)
ssr_exp = np.sum(residuals_exp**2)
# --- RMSE ---
rmse_lin1 = np.sqrt(ssr_lin1 / dof_lin1)
rmse_lin2 = np.sqrt(ssr_lin2 / dof_lin2)
rmse_quadr = np.sqrt(ssr_quadr / dof_quadr)
rmse_exp = np.sqrt(ssr_exp / dof_exp)
# --- Chi² ---
chi2_lin1 = np.sum((residuals_lin1 / y_err) ** 2)
chi2_lin2 = np.sum((residuals_lin2 / y_err) ** 2)
chi2_quadr = np.sum((residuals_quadr / y_err) ** 2)
chi2_exp = np.sum((residuals_exp / global_mean["uncertainty"].values) ** 2)
chi2_red_lin1 = chi2_lin1 / dof_lin1
chi2_red_lin2 = chi2_lin2 / dof_lin2
chi2_red_quadr = chi2_quadr / dof_quadr
chi2_red_exp = chi2_exp / dof_exp
# --- R² und Adjusted R² ---
def r2_adj(y_true, y_pred, p):
r2 = r2_score(y_true, y_pred)
n = len(y_true)
return r2, 1 - (1-r2)*(n-1)/(n-p-1)
r2_lin1, r2adj_lin1 = r2_adj(y, model_lin1[0][0]*x + model_lin1[0][1], 2)
r2_lin2, r2adj_lin2 = r2_adj(y_1980, model_lin2[0][0]*x_1980 + model_lin2[0][1], 2)
r2_quadr, r2adj_quadr = r2_adj(y, quadratic_fit(x,*popt), 3)
r2_exp, r2adj_exp = r2_adj(ydata, exp_model(xdata, *popt_exp), len(popt_exp))
# --- Ergebnisse in Tabelle ---
results = pd.DataFrame({
"Modell": ["Linear (ges. Reihe)", "Linear (ab 1981)", "Quadratisch", "Exponentiell"],
"Freiheitsgrade": [dof_lin1, dof_lin2, dof_quadr, dof_exp],
"SSR": [ssr_lin1, ssr_lin2, ssr_quadr, ssr_exp],
"RMSE": [rmse_lin1, rmse_lin2, rmse_quadr, rmse_exp],
"Chi²": [chi2_lin1, chi2_lin2, chi2_quadr, chi2_exp],
"Chi²_red": [chi2_red_lin1, chi2_red_lin2, chi2_red_quadr, chi2_red_exp],
"R²": [r2_lin1, r2_lin2, r2_quadr, r2_exp],
"R²_korr": [r2adj_lin1, r2adj_lin2, r2adj_quadr, r2adj_exp]
})
print(results.to_string(index=False, float_format="%.3f"))
plt.figure(figsize=(10,5))
plt.rcParams['font.size'] = 10
plt.ylabel("Residuen")
plt.xlabel("Jahr")
# Residuenplots
plt.plot(x, residuals_lin1, label='Linear (ges. Reihe)', color="C0")
plt.plot(x_1980, residuals_lin2, label='Linear (ab 1981)', color="C1")
plt.plot(x, residuals_quadr, label='Quadratisch', color="C2")
plt.plot(global_mean["Year"], residuals_exp, label='Exponentiell', color="C3")
# Standardfehler (RMSE) als horizontale Linien
plt.axhline(rmse_lin1, color='C0', linestyle='--', alpha=0.7, label='RMSE Linear (ges.)')
plt.axhline(-rmse_lin1, color='C0', linestyle='--', alpha=0.7)
plt.axhline(rmse_lin2, color='C1', linestyle='--', alpha=0.7, label='RMSE Linear (ab 1981)')
plt.axhline(-rmse_lin2, color='C1', linestyle='--', alpha=0.7)
plt.axhline(rmse_quadr, color='C2', linestyle='--', alpha=0.7, label='RMSE Quadratisch')
plt.axhline(-rmse_quadr, color='C2', linestyle='--', alpha=0.7)
plt.axhline(rmse_exp, color='C3', linestyle='--', alpha=0.7, label='RMSE Exponentiell')
plt.axhline(-rmse_exp, color='C3', linestyle='--', alpha=0.7)
# Legende, Gitter, Speichern
plt.legend()
plt.grid(alpha=0.3)
plt.title("Residuenvergleich der Modelle")
plt.savefig('klima_residuen.png')
plt.savefig('klima_residuen.pdf')
plt.show()
Modell Freiheitsgrade SSR RMSE Chi² Chi²_red R² R²_korr
Linear (ges. Reihe) 143 5.255 0.192 84.072 0.588 0.763 0.760
Linear (ab 1981) 43 0.494 0.107 7.899 0.184 0.865 0.858
Quadratisch 142 2.086 0.121 33.375 0.235 0.906 0.904
Exponentiell 142 1.926 0.116 30.813 0.217 0.913 0.911
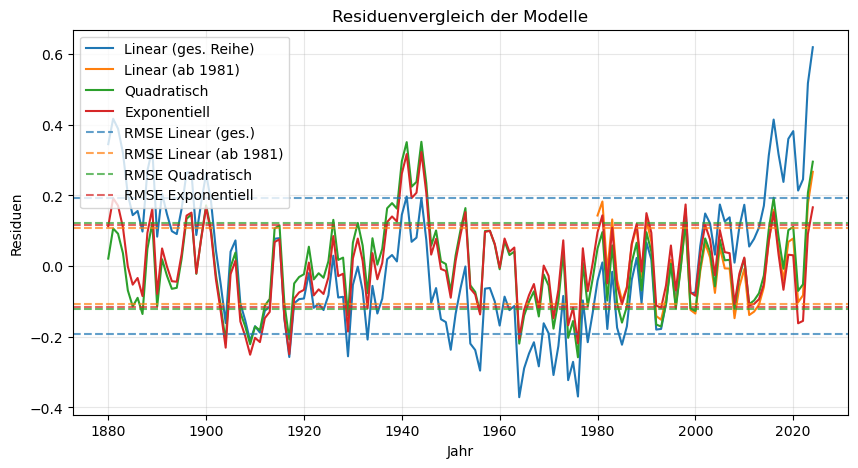
Vergleicht man die jeweiligen Werte miteinander, so zeigt sich:
In allen Fällen sind die Residuen gleichmäßig um Null verteilt – alle Modelle liefern also eine gute Approximation.
Das zweite lineare Modell (angepasst ab dem Jahresbereich 1981) erzielt gute Ergebnisse, der Standardfehler ist der kleinste im Vergleich zu anderen Modellen. Jedoch muss man hier berücksichtigen, dass weniger Daten benutzt werden als in den anderen Zeitserien und damit Werte verfälscht werden im direkten Vergleich.
Betrachtet man den gesamten Jahresbereich, liefern das quadratische und expxonentielle Modell die besten Ergebnisse.
Alle reduzierten \(\chi^2\)-Werte liegen unter 1. Das deutet darauf hin, dass die angenommenen Fehlerbalken zu groß gewählt worden sind und das Modell zu gut passt. Alle Modelle sind akzeptabel, aber unsere geschätzten Unsicherheiten von 0,25 Kelvin dominieren.
Fehler der Vorhersagen#
Im Folgenden berechnen wir den Fehler für die Vorhersage für das Jahre 2050. Da Korrelationen zwischen den Modellparametern auftreten werden diese miteinbezogen.
import numpy as np
# Jahr für Vorhersage
x_val = 2050
x_exp = (x_val - 1880) / 100 # normiert für exp
# --- LINEAR (ges. Reihe) ---
p_lin1, cov_lin1 = np.polyfit(x, y, 1, cov=True)
y_pred_lin1 = np.polyval(p_lin1, x_val)
# Unsicherheit: Var(f) = J C J^T
J_lin1 = np.array([x_val, 1.0]) # [∂f/∂m, ∂f/∂b] = [x, 1]
var_lin1 = J_lin1 @ cov_lin1 @ J_lin1.T
sigma_lin1 = np.sqrt(var_lin1)
# --- LINEAR (ab 1981) ---
p_lin2, cov_lin2 = np.polyfit(x_1980, y_1980, 1, cov=True)
y_pred_lin2 = np.polyval(p_lin2, x_val)
J_lin2 = np.array([x_val, 1.0])
var_lin2 = J_lin2 @ cov_lin2 @ J_lin2.T
sigma_lin2 = np.sqrt(var_lin2)
# --- QUADRATISCH ---
p_quadr, cov_quadr = np.polyfit(x, y, 2, cov=True)
y_pred_quadr = np.polyval(p_quadr, x_val)
# Ableitungen: f(x) = ax^2 + bx + c
J_quadr = np.array([x_val**2, x_val, 1.0])
var_quadr = J_quadr @ cov_quadr @ J_quadr.T
sigma_quadr = np.sqrt(var_quadr)
# --- EXPONENTIELL ---
# exp_model(x) = a * exp(bx) + c
a, b, c = popt_exp
cov_exp = pcov_exp
y_pred_exp = exp_model(x_exp, *popt_exp)
J_exp = np.array([
np.exp(b * x_exp), # ∂f/∂a
a * x_exp * np.exp(b * x_exp), # ∂f/∂b
1.0 # ∂f/∂c
])
var_exp = J_exp @ cov_exp @ J_exp.T
sigma_exp = np.sqrt(var_exp)
# --- Ergebnisse ---
print(f"Vorhersage 2050 Linear (ges. Reihe): {y_pred_lin1:.3f} ± {sigma_lin1:.3f}")
print(f"Vorhersage 2050 Linear (ab 1981): {y_pred_lin2:.3f} ± {sigma_lin2:.3f}")
print(f"Vorhersage 2050 Quadratisch: {y_pred_quadr:.3f} ± {sigma_quadr:.3f}")
print(f"Vorhersage 2050 Exponentiell: {y_pred_exp:.3f} ± {sigma_exp:.3f}")
Vorhersage 2050 Linear (ges. Reihe): 0.873 ± 0.041
Vorhersage 2050 Linear (ab 1981): 1.543 ± 0.061
Vorhersage 2050 Quadratisch: 1.614 ± 0.057
Vorhersage 2050 Exponentiell: 2.396 ± 0.168
Die Fehler steigen mit: weniger Daten, mehr Parameter, stärkeren Korrelationen, oder hohe Sensitivität des Modells (exponentiell). Das erklärt die Unterschiede: ±0.04 (linear, viele Daten) bis ±0.17 (exp, sensitiv und korreliert).


