Übertragungsfunktion

Die Übertragungsfunktion ist eine der wichtigsten Funktionen, um Messsysteme im Frequenzbereich zu charakterisieren. Sie ist das Verhältnis von Ausgangs- zu Eingangssinal in dynamischen Messsystemen, und damit das äquivalent zur Kennlinie in stationären Messsystemen. Um sie zu bestimmen, benötigen wir die Kenntnis über das dynamische Verhalten eines Messsystems, z.B. in Form einer Differentialgleichung (DGL) oder durch Messungen, die wir jeweils in den Fourier-Raum transformieren.

Notation

Wenn \(x(t)\) das Eingangssignal im Zeit-Raum ist, dann bezeichnen wir mit \(X(j \omega)\), bzw. \(X(s)\) das Eingangssignal im Frequenz- bzw. Laplaceraum. Hier ist \(j\) wieder die komplexe Zahl. Das Ausgangssignal \(y(t)\) wird analog dazu mit \(Y(j \omega)\) bzw. \(Y(s)\) bezeichnet. Es hat sich eingebürgert, dass Zeitsignale mit kleinen Buchstaben, \(x\), bezeichnet werden und Signale im Frequenzbereich mit großen Buchstaben, \(X\).

Erinnerung Transformationen

• Fourier-Transformation:

  \[\mathcal F(x(t)) = X(j\omega) = \int_{-\infty}^{\infty} x(t) \mathrm e^{-j \omega t} dt\]

• Laplace-Transformaton, mit der komplexen Frequenz \(s = \sigma + j\omega\):

  \[\mathcal L(x(t)) = X(s) = \int_{0}^{\infty} x(t) \mathrm e^{-st} dt\]

Abb. 54 Signale und Messsystem im Zeit- bzw. Frequenzraum.

Die Übertragungsfunktion eines Messsystems, \(G(j \omega)\) bzw. \(G(s)\), kann also wie folgt aus den Fourier-Transformierten der Ein- und Ausgangssignale ausgedrückt werden:

\[G(j \omega) = \frac{Y(j \omega)}{X(j \omega)}\]

bzw. im Laplaceraum:

\[G(s) = \frac{Y(s)}{X(s)}\]

Im Folgenden werden wir zwischen Fourier- und Laplaceraum nicht unbedingt unterscheiden. Die Herleitung der Übertragungsfunktion ist für beide Räume die gleiche, lediglich die Variable ändert sich von \(j \omega\) zu \(s\). Im Allgmeinen gilt:

• Die Fourier-Transformation (FT) wird bei kontinuierlichen Signalen verwendet. Für eine FT muss das Signal integrierbar sein, was für einen Sprung,or Rampe nicht gilt, da hier das Integral gegen unendlich läuft.

• Die Laplace-Transformation wird bei Reaktionen auf diskrete Funktionen verwendet, wie z.B. Stufenfunktion, Impulsfunktion oder Delta-Dirac-Puls, die mittels FT nicht analysiert werden können.

Herleitung der Übertragungsfunktion

Anhand unseres Beispiels, dem Tiefpass 1. Ordnung, wollen wir die Übertragungsfunktion einmal herleiten.

Eine Möglichkeit die Übertragungsfunktion zu bestimmen, ist es die DGL aus dem vorherigen Kapitel in den Frequenzraum zu transformieren. Aus

\[\tau \frac{du_\mathrm a (t)}{dt} + u_\mathrm a (t) = u_\mathrm e (t)\]

und dem Einsetzen von \(u_\mathrm e (t) \rightarrow U_e(j \omega)\), \(u_\mathrm a (t) \rightarrow U_a(j \omega)\) und \(\dot u_\mathrm a (t) \rightarrow j \omega U_a(j \omega)\) wird

\[\tau j \omega U_\mathrm a(j \omega) + U_\mathrm a (j \omega) = U_\mathrm e (j \omega)\]

Die DGL wird nach \(U_\mathrm a(j \omega) / U_\mathrm e(j \omega)\) umgestellt, um die Übertragungsfunktion zu erhalten:

\[G(j \omega) = \frac{U_\mathrm a(j \omega)}{U_\mathrm e(j \omega)} = \frac{1}{1+\tau j \omega}\]

mit \(\gamma = \frac{1}{RC} = \frac{1}{\tau}\)

Übertragungsfunktion

• Die Übertragungsfunktion ist das Verhältnis von Ausgangs- zu Eingangssinal. Im Allgemeinen setzt man eine Impulsanregung ein, \(X(s) = 1\).

• Die Übertragungsfunktion kann aus der DGL im Frequenzraum bestimmt werden.

• Die Übertragungsfunktion ist also eine komplexe Zahl und hat somit eine Amplitude und Phase!

• Die Übertragungsfunktion kann außerdem experimentell bestimmt werden, sodass keine theoretischen Herleitungen nötig sein.

• Mittels Faltung kann die Übertragung von beliebigen Messsignalen vorhergesagt werden.

Bode Diagramm

Die komplexe Übertragungsfunktion wird in sogenannten Bode-Diagrammen dargestellt. Ein Bode-Diagramm besteht aus zwei Diagrammen, die Amplitude und Phase der Übertragungsfunktion aufzeigen. Anhand diesen Diagrammen kann man das Verhalten von Messsystemen sehr gut charakterisieren und viele Eigenschaften ablesen.

Zur Veranschaulichung verwenden bleiben wir weiterhin beim Tiefpass 1. Ordnung.

\[G(j \omega) = \frac{U_\mathrm a(j \omega)}{U_\mathrm e(j \omega)} = \frac{1}{1+RC j \omega}\]

Um Amplitude und Phase der komplexen Übertragungsfunktion ablesen zu können, müssen wir die komplexe Zahl so umformen, dass Real- und Imaginärteil abgelesen werden können. Hierfür erweitern wir \(G\) typischer mit dem komplex Konjugierten:

\[\begin{split} \begin{align} G(j \omega) &= \frac{1}{1+RC j \omega} \\ &= \frac{1}{1+RC j \omega} \cdot \frac{1-RC j \omega}{1-RC j \omega}\\ &= \frac{1-RC j \omega}{1- (RC \omega)^2} \\ &= \frac{1}{1- (RC \omega)^2} - j\frac{ RC \omega}{1- (RC \omega)^2} \end{align} \end{split}\]

Die Amplitude wird wiefolgt berechnet, wobei \(\tau = RC =: 1/\omega_0\). Die Einheit beträgt typischerweise dB.

\[|G(j \omega)| = \sqrt{\mathrm{Re}^2 + \mathrm{Im}^2} = \frac{1}{\sqrt{1+\left(\frac{\omega}{\omega_0}\right)^2}}\]

Die Phase wird wiefolgt berechnet, wobei \(\tau = RC =: 1/\omega_0\). Die Einheit beträgt typischerweise Grad.

\[\phi(\omega) = \arctan\left(\frac{\mathrm{Im}}{\mathrm{Re}}\right) = \arctan\left(-\frac{\omega}{\omega_0}\right)\]

Sowohl Amplitude als auch Phase sind hängen von der Frequenz \(\omega\) ab! Daher nennt man die Fuktionen für Amplitude und Phase auch Amplitudengang bzw. Phasengang. Beide zusammengenommen bilden den Frequenzgang eines Systems und werden häufig zusammen geplottet, im sogenannten Bode-Diagramm.

Bode Diagramm

• Das Bode-Diagramm bietet eine einfache Darstellungsweise der Frequenzantwort eines Messsystems

• Das Bode-Diagramm ist ein Werkzeug um die Stabilitätseigenschaften von Kontrollsystemem zu analysieren.

Die folgende Darstellung zeigt das Bode-Diagramm von zwei Tiefpässen 1. Ordnung, die jeweils eine unterschiedliche Zeitkonstante \(\tau\) besitzen. Diese kann über \(R\) und \(C\) verändert werden. Im Vergleich dazu ist auf der rechten Zeite die Sprungantwort der beiden Tiefpässe im Zeit-Raum dargestellt.

Show code cell source Hide code cell source

import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')

# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['axes.grid']= True     # defaults to False but xkcd() makes it False
plt.rcParams['grid.linewidth']= 0.8  # defaults to 0.8
plt.rcParams['font.size'] = 10; # Schriftgröße

# Transfer Funktion Tiefpass:
num = np.array([1])
den = np.array([1 , 1])
H = signal.TransferFunction(num , den)
num = np.array([1])
den = np.array([2 , 1])
H2 = signal.TransferFunction(num , den)

# Bode-Plot:
w, mag, phase = signal.bode(H)
w2, mag2, phase2 = signal.bode(H2)

# Plotting
# Supplot2grid approach

fig, ax = plt.subplots(figsize=(10,5))
ax1 = plt.subplot2grid((2,2), (0,0)) # topleft
ax3 = plt.subplot2grid((2,2), (0,1), rowspan=2)            # right
ax2 = plt.subplot2grid((2,2), (1,0))                       # bottom left

ax1.semilogx(w, mag, color='tab:blue', label = r'$G_1(s) = \frac{1}{s+1} \rightarrow \tau_1 = 1\, s $')
ax1.semilogx(w2, mag2, color='tab:red', label = r'$G_2(s) = \frac{1}{2s+1} \rightarrow \tau_2 = 2\, s $')

ax1.axhline(y = -3, color='k', ls = '--', lw = 1)
ax1.axvline(x = 1, color='tab:blue', ls = '--', lw = 1)
ax1.axvline(x = 0.5, color='tab:red', ls = '--', lw = 1)
ax1.set_xticks([1e-2, 1e-1, 0.5, 1, 10], labels = [r'$10^{-2}$', r'$10^{-1}$', '0.5', '1', '10'])
ax1.set_title("Bode Plot")
ax1.grid(True, lw=0.5, zorder=0, ls = '--', which='major', axis='both')
ax1.grid(True, lw=0.5, zorder=0, ls = '--', which='minor', axis='both')
ax1.set_ylabel("Amplitude (dB)")
ax1.legend()


# Plotting
ax2.semilogx(w, phase, color='tab:blue')
ax2.semilogx(w2, phase2, color='tab:red')
ax2.axhline(y = -45, color='k', ls = '--', lw = 1)
ax2.axvline(x = 1, color='tab:blue', ls = '--', lw = 1)
ax2.axvline(x = 0.5, color='tab:red', ls = '--', lw = 1)
ax2.set_yticks([0,-45,-90])
ax2.set_xticks([1e-2, 1e-1, 0.5, 1, 10], labels = [r'$10^{-2}$', r'$10^{-1}$', '0.5', '1', '10'])
ax2.grid(True, lw=0.5, zorder=0, ls = '--', which='minor', axis='both')
ax2.grid(True, lw=0.5, zorder=0, ls = '--', which='major', axis='both')
ax2.set_xlabel("Frequenz (Hz)")
ax2.set_ylabel('Phase (deg)')


# Sprungantwort:
t, y = signal.step(H)
t2, y2 = signal.step(H2)

# Plotting
ax3.plot(t, y, color='tab:blue', label = r'$\frac{u_a(t)}{u_0} = 1- e^{-\left(\frac{t}{\tau = 1\, s}\right)}$')
ax3.plot(t2, y2, color='tab:red', label = r'$\frac{u_a(t)}{u_0} = 1- e^{-\left(\frac{t}{\tau = 2\, s}\right)}$')
ax3.axhline(y = 1.0, color='k', ls = '--', lw = 1)
ax3.axhline(y = 0.63, color='k', ls = '--', lw = 1)
ax3.axvline(x = 1, color='tab:blue', ls = '--', lw = 1)
ax3.axvline(x = 2, color='tab:red', ls = '--', lw = 1)
ax3.set_yticks([1.0, 0.63], labels = ['100%', '63%'])
#ax3.set_yticklabels(['100%', '63%'])
ax3.set_xticks([1,2], labels = [r'$\tau_1$',r'$\tau_2$'])
#ax3.set_xticklabels([r'$\tau_1$',r'$\tau_2$'])
ax3.set_title("Sprungantwort eines Tiefpasses")
ax3.set_xlabel("Zeit t")
ax3.set_ylabel(r'$u_a(t)/u_0$')
ax3.grid(True, lw=0.5, zorder=0, ls = '--', which='minor', axis='both')
ax3.grid(True, lw=0.5, zorder=0, ls = '--', which='major', axis='both')
ax3.legend()

plt.tight_layout()

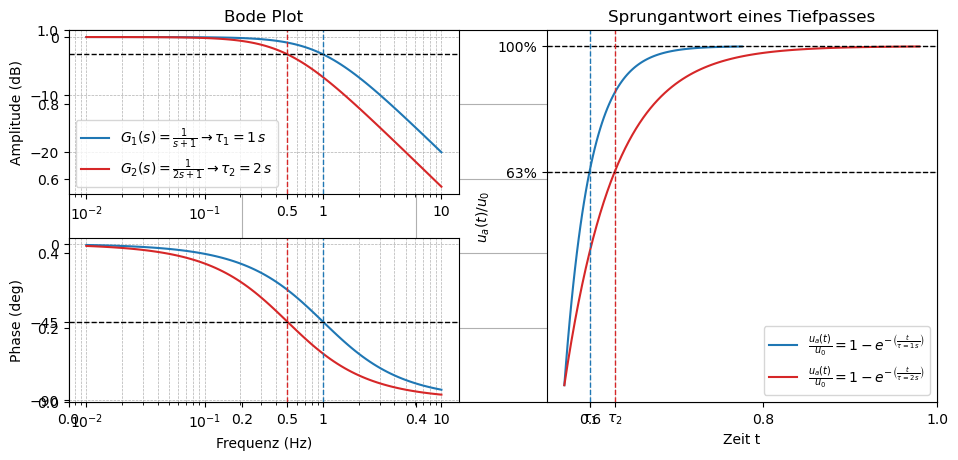
Grenzfrequenz (Bandbreite)

Aus dem Bode-Diagramm kann man die sogenannte Grenzfrequenz (Bandbreite, cut-off Frequenz) eines Messsystems direkt ablesen. Die Grenzfrequenz ist so definiert, dass die Amplitude des Eingangssignals auf

\[1/\sqrt{2} = 0,707 = -3\,\mathrm{dB}\]

abfällt und ist für einen Tiefpass 1. Ordnung bei \(\omega_0 = 1/\tau\).

Warnung

Obwohl viele Messsysteme über die sogenannte Bandbreite charakterisiert sind, darf man nicht vergessen, dass Signale bei dieser Grenzfrequenz bereits eine Abschächung von -3dB erfahren und somit signifikante Amplitudenverluste in Höhe von 29% verursachen.

Je höher die Frequenz, desto höher die Verluste (bei dem hier dargestellten Tiefpassfilter!). Das heißt der Fehler, der bei einer Messung gemacht wird, ist frequenzabhängig!

In der Akustik kann man damit leben, da man kaum einen Unterschied hört. In der Messtechnik bei der Überwachung von schwingenden Maschinenteilen oder der Ermittlung von Rundlaufabweichungen von drehenden Wellen ist solch ein Ampitudenabfall meist nicht zu akzeptieren. Üblicherweise sollte man andere Grenzfrequenzen separat angeben, die 90% oder 99% der Signalstärke durchlassen.

Verhalten von Systemen 2. Ordnung

Der Vollständigkeitshalber wollen wir uns noch ganz kurz die Bode-Diagramme von Systemen 2. Ordnung ansehen. Auf eine mathematische Beschreibung wollen wir an dieser Stelle aber verzichten.

Bei Systemen 1. Ordnung handelt es sich um Systeme mit Energiespeicher, also alle Systeme die irgendwie warm werden. Bei Systemen 2. Ordnung hat man zwei gekoppelte Energiespeicher, die Energie unter Umständen periodisch austauschen können. Hier findet man dann immer einen zusätzlichen Term in der DGL der die Dämpfung des Systems beschreibt.

Um ein System 1. Ordnung von einem System 2. Ordnung zu unterscheiden, kann man sich das Bode-Diagramm (links im nachfolgenden Bild) ansehen. Bei Systemen 1. Ordnung fällt die Amplitude innerhalb einer Frequenzdekade (also ein Faktor 10) um -20 dB ab, bei Systemen 2. Ordnung um -40 dB (Übung: Warum?). Auch die zeitliche Verzögerung, also die Phase des Eingangssignals, erfährt ebenfalls einen steileren Abfall.

Show code cell source Hide code cell source

import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')

# MatplotLib Settings:
plt.style.use('default') # Matplotlib Style wählen
#plt.xkcd()
plt.rcParams['axes.grid']= True     # defaults to False but xkcd() makes it False
plt.rcParams['grid.linewidth']= 0.8  # defaults to 0.8
plt.rcParams['font.size'] = 10; # Schriftgröße

#fig, ax = plt.subplots(figsize=(8,5))
ax1 = plt.subplot2grid((2,2), (0,0)) # topleft
ax3 = plt.subplot2grid((2,2), (0,1), rowspan=1)            # right
ax2 = plt.subplot2grid((2,2), (1,0))  
ax4 = plt.subplot2grid((2,2), (1,1))  

for i, ax in enumerate(fig.axes):
    ax.set_xlim(1e-2,100)
        
w2 = np.logspace(-3,2,200)

# Transfer Funktion Tiefpass 1. Ordnung:
K = 1
T = 1
num = np.array([K])
den = np.array([T , 1])
H = signal.TransferFunction(num , den)
w, mag, phase = signal.bode(H,w2)
ax1.semilogx(w, mag, color='tab:blue')
ax1.set_yticks([0, -20, -40, -60],['$0$','-20', '-40', '-60'])
ax1.set_xticks([0.01/T,0.1/T,1/T,10/T,100/T], ['0.01','0.1','1','10','100'])
ax1.grid(True, lw=0.5, zorder=0, ls = '--', which='major', axis='both')
ax1.set_ylabel("Amplitude (dB)")
ax1.set_ylim(-80,10)
ax1.set_title('Tiefpass 1. Ordg.')

ax2.semilogx(w, phase, color='tab:blue')
ax2.set_yticks([0,-90, -180])
ax2.set_xticks([0.01/T,0.1/T,1/T,10/T,100/T], ['0.01','0.1','1','10','100'])
ax2.grid(True, lw=0.5, zorder=0, ls = '--', which='major', axis='both')
ax2.set_xlabel("Frequenz $f/f_0$")
ax2.set_ylabel('Phase (deg)')

# Transfer Funktion Tiefpass 2. Ordnung:
K = 1
T = 1
D = 0.2
num = np.array([K])
den = np.array([T ,2*D*T, 1])
H = signal.TransferFunction(num , den)
w, mag, phase = signal.bode(H,w2)

ax3.semilogx(w, mag, color='tab:red')
ax3.set_yticks([0, -20, -40, -60],['$0$','-20', '-40', '-60'])
ax3.set_xticks([0.01/T,0.1/T,1/T,10/T,100/T], ['0.01','0.1','1','10','100'])
ax3.grid(True, lw=0.5, zorder=0, ls = '--', which='major', axis='both')
ax3.set_ylabel("Amplitude (dB)")
ax3.set_ylim(-80,10)
ax3.set_title('Tiefpass 2. Ordg.')

ax4.semilogx(w, phase, color='tab:red')
ax4.set_yticks([0,-90, -180])
ax4.set_xticks([0.01/T,0.1/T,1/T,10/T,100/T], ['0.01','0.1','1','10','100'])
ax4.grid(True, lw=0.5, zorder=0, ls = '--', which='major', axis='both')
ax4.set_xlabel("Frequenz $f/f_0$")
ax4.set_ylabel('Phase (deg)')

plt.tight_layout()

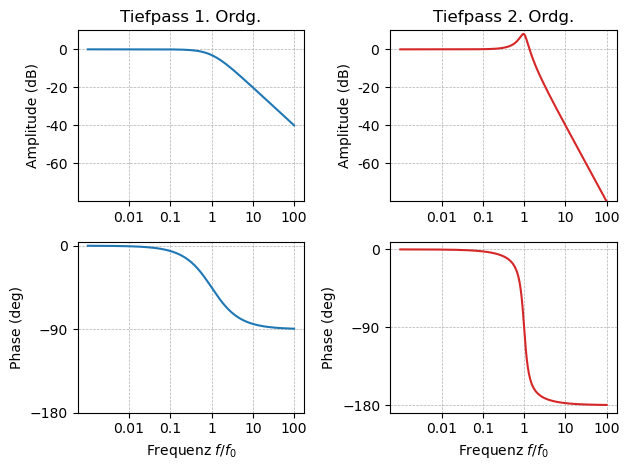
Beispiele von Bode-Diagrammen

Einige Beispiele zu Systemen mit Verzögerungs, Dämpfungs bzw. auch integrierendem Verhalten sind in nachfolgenden Plots dargestellt. In der Literatur findet man häufig tabellarische Zusammenfassungen verschiedener Messsysteme inklusive Übertragungsfunktion und Bode-Diagramm, damit die DGL nicht jedes mal neu hergeleitet werden müssen.

Abb. 55 Verstärker P DGL: \(u_a = K \cdot u_e\)’, r’\(G(s) = K \)‘,r’\(\frac{u_a(t)}{K\cdot u_e} = 1\)

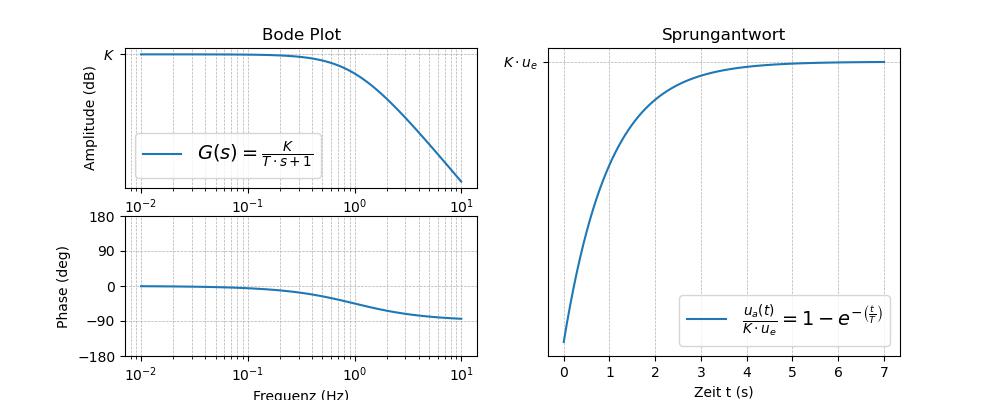
Abb. 56 Tiefpass PT\(_1\) DGL: \(T \cdot \dot u_a + u_a = K \cdot u_e\)’, r’\(G(s) = \frac{K}{T \cdot s+1} \)‘,r’\(\frac{u_a(t)}{K\cdot u_e} = 1- e^{-\left(\frac{t}{T}\right)}\)

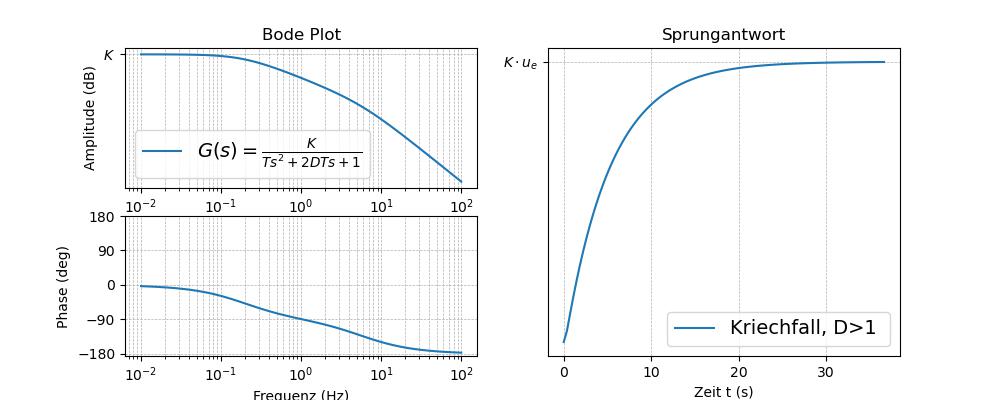
Abb. 57 Tiefpass PT\(_2\) DGL: \(T \cdot \ddot u_a + 2DT \cdot \dot u_a + u_a = K \cdot u_e\)’, r’\(G(s) = \frac{K}{T s^2 + 2DT s+1} \)‚,r’Kriechfall, D>1

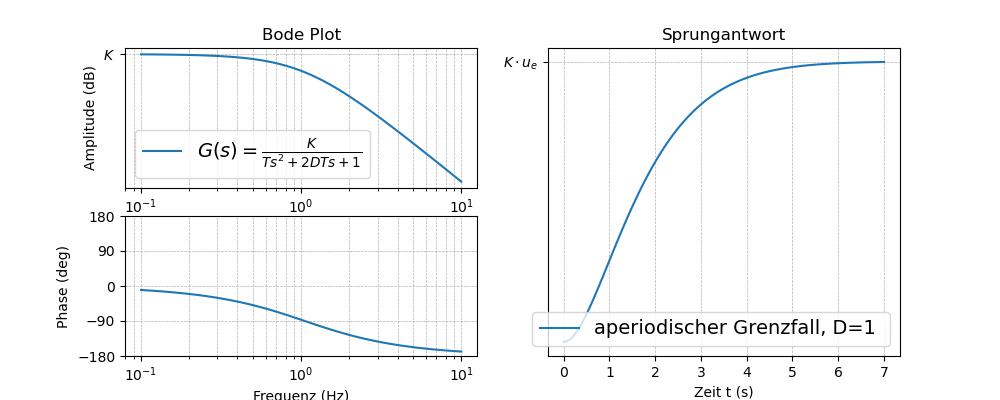
Abb. 58 Tiefpass PT\(_2\) DGL: \(T \cdot \ddot u_a + 2DT \cdot \dot u_a + u_a = K \cdot u_e\)’, r’\(G(s) = \frac{K}{T s^2 + 2DT s+1} \)‚,r’aperiodischer Grenzfall, D=1

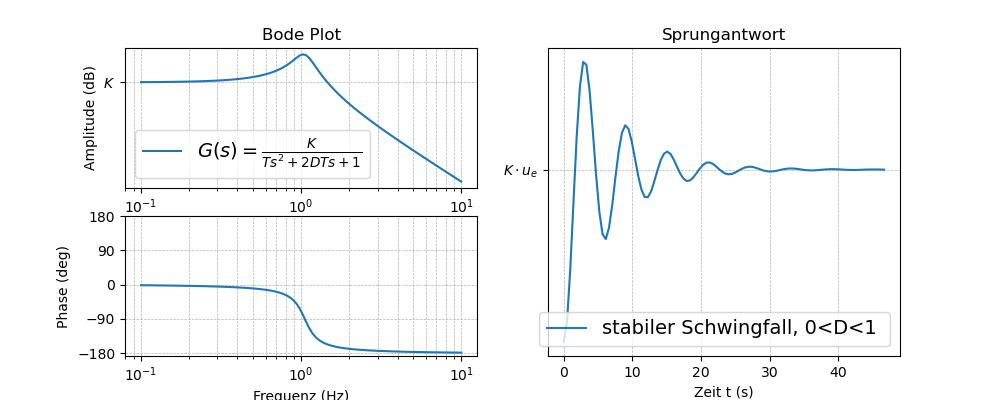
Abb. 59 Tiefpass PT\(_2\) DGL: \(T \cdot \ddot u_a + 2DT \cdot \dot u_a + u_a = K \cdot u_e\)’, r’\(G(s) = \frac{K}{T s^2 + 2DT s+1} \)‚,r’stabiler Schwingfall, 0<D<1

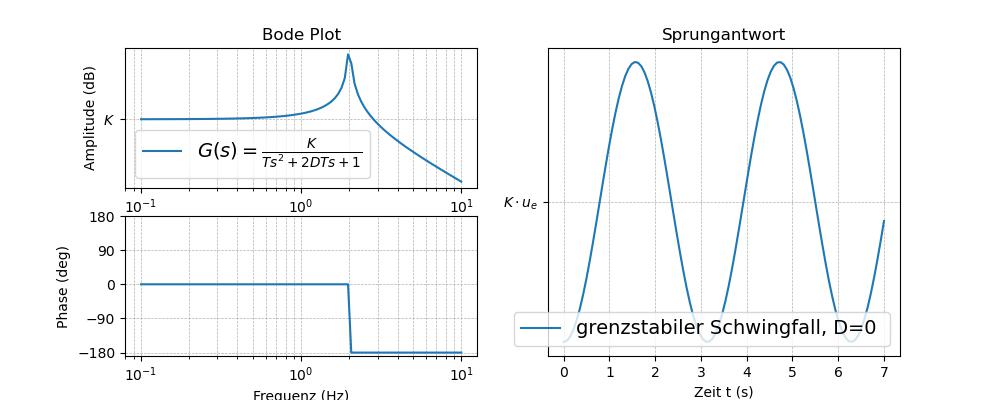
Abb. 60 Tiefpass PT\(_2\) DGL: \(T \cdot \ddot u_a + 2DT \cdot \dot u_a + u_a = K \cdot u_e\)’, r’\(G(s) = \frac{K}{T s^2 + 2DT s+1} \)‚,r’grenzstabiler Schwingfall, D=0

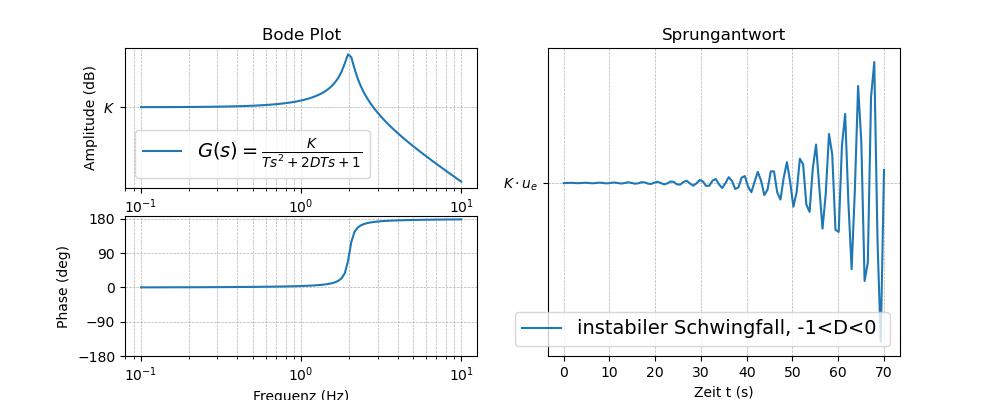
Abb. 61 Tiefpass PT\(_2\) DGL: \(T \cdot \ddot u_a + 2DT \cdot \dot u_a + u_a = K \cdot u_e\)’, r’\(G(s) = \frac{K}{T s^2 + 2DT s+1} \)‚,r’instabiler Schwingfall, -1<D<0

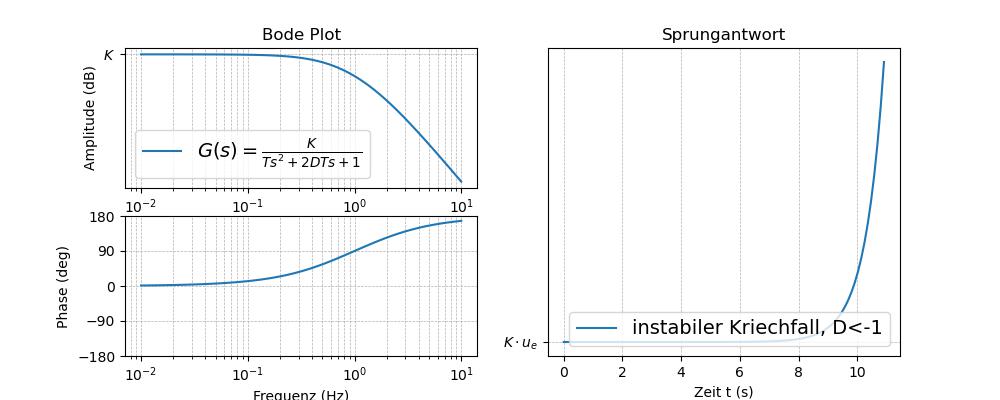
Abb. 62 Tiefpass PT\(_2\) DGL: \(T \cdot \ddot u_a + 2DT \cdot \dot u_a + u_a = K \cdot u_e\)’, r’\(G(s) = \frac{K}{T s^2 + 2DT s+1} \)‚,r’instabiler Kriechfall, D<-1

Verhalten von Testfunktionen am Tiefpass

Im Folgenden Bild grafisch dargestellt, wie verschiedene Signale durch einen Tiefpass mit der Übertragungsfunktion

\[G(s) = \frac{1}{s+1}\]

verfälscht werden können, in dem hohe Frequenzanteile abgeschwächt werden. Auch hier erkennt man wieder einen Zusammenhang zu den Fourierreihen, wenn man sich das Rechtecksignal ansieht. Eine Reihe von Rechteckpulsen benötigt eine hohe Anzahl von Sinusfunktionen bei höheren harmonischen der Grundfrequenz, um möglichst steile Flankenübergänge zu erhalten. Eine Filterung dieser hohen Frequenzanteile sorgt für eine deutliche Verzerrung des Signals. Bei sinusförmirgen Signalen hingegen wird nur die Amplitude abgeschwächt und es findet zusätzlich, je nach Frequenz, eine zeitlich Verzögerung statt, d.h. die Signale sind phasenverschoben um bis zu -90°.

• Je größer \(\tau\), desto langsamer ist das System

• Je kleiner \(\tau\), desto schneller ist das System

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
import warnings
from matplotlib.animation import FuncAnimation
from IPython.display import HTML

warnings.filterwarnings('ignore')

# Grundlegende Parameter
SAMPLE_RATE = 500.0  # Hertz
DURATION = 10  # Sekunden
t = np.linspace(0, DURATION, int(SAMPLE_RATE * DURATION), endpoint=False)
u = 1.0
    
plt.figure(figsize=(10, 3))
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(10,3))

def animate_filtered_signals(filter_frequenz):
    ax[0].clear()  # Clear the previous frame
    ax[1].clear()  # Clear the previous frame
    ax[2].clear()  # Clear the previous frame

    # Tiefpass-Filter konfigurieren
    order = 1
    b, a = signal.butter(order, filter_frequenz, 'low', analog=True)
    sos = signal.butter(order, filter_frequenz, 'low', fs=SAMPLE_RATE, output='sos')
    w, h = signal.freqs(b, a)

    
    # Verschiedene Signale und ihre gefilterten Versionen
    # 2.0 Hz Sinus Signal + Gefiltert
    ff = 8.0
    y_sin1 = u * np.sin(2 * np.pi * ff * t)
    y_sin1_filt = signal.sosfilt(sos, y_sin1)

    ax[0].set_title("Eingangssignal f =%5.1f Hz" %ff)
    ax[2].set_title("Ausgangssignal A =%5.1f V" %np.max(y_sin1_filt))

    ax[0].plot(t,y_sin1)
    ax[2].plot(t,y_sin1, color = 'tab:blue', alpha = 0.5)
    ax[2].plot(t,y_sin1_filt, color  = 'tab:red')
    
    ax[0].set_xlim([0,1])
    ax[2].set_xlim([0,1])
    ax[0].set_ylim([-1.1,1.1])
    ax[2].set_ylim([-1.1,1.1])

    # Bode Plot
    ax[1].semilogx(w, 20 * np.log10(abs(h)), color = 'tab:red', lw = 2)
    ax[1].axhline(y = -3, color='k', ls = '--', lw = 1)
    ax[1].axvline(x = filter_frequenz, color='tab:red', ls = '-', lw = 1)
    ax[1].axvline(x = ff, color='tab:blue', ls = '-', lw = 1)

    #ax[1].set_xticks([1e-2, 1e-1, 0.5, 1, 10], labels = [r'$10^{-2}$', r'$10^{-1}$', '0.5', '1', '10'])
    ax[1].set_title("Tiefpass: f =%5.1f Hz" %filter_frequenz)
    ax[1].grid(True, lw=0.5, zorder=0, ls = '--', which='major', axis='both')
    ax[1].grid(True, lw=0.5, zorder=0, ls = '--', which='minor', axis='both')
    ax[1].set_ylabel("Amplitude (dB)")
    ax[1].set_xlim([1e-1,100])
    ax[1].set_ylim([-25,1])

ani = FuncAnimation(fig, animate_filtered_signals, frames=range(1, 51), repeat=False)

# Display the animation
plt.tight_layout()
plt.subplots_adjust(wspace=0.3)
plt.subplots_adjust(top=0.85)
plt.close()
ani.save('LP_sinus.mp4', writer='ffmpeg', dpi=300)
HTML(ani.to_jshtml())

Once Loop Reflect

<Figure size 1000x300 with 0 Axes>

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
import warnings
from matplotlib.animation import FuncAnimation
from IPython.display import HTML

warnings.filterwarnings('ignore')

# Grundlegende Parameter
SAMPLE_RATE = 500.0  # Hertz
DURATION = 10  # Sekunden
t = np.linspace(0, DURATION, int(SAMPLE_RATE * DURATION), endpoint=False)
u = 1.0
    
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(10,3))

def animate_filtered_signals(filter_frequenz):
    ax[0].clear()  # Clear the previous frame
    ax[1].clear()  # Clear the previous frame
    ax[2].clear()  # Clear the previous frame

    # Tiefpass-Filter konfigurieren
    order = 1
    b, a = signal.butter(order, filter_frequenz, 'low', analog=True)
    sos = signal.butter(order, filter_frequenz, 'low', fs=SAMPLE_RATE, output='sos')
    w, h = signal.freqs(b, a)

    # 4 Hz Rechteck Signal + Gefiltert
    ff = 4
    y_rect1 = signal.square(2 * np.pi * ff * t)
    y_rect1_filt = signal.sosfilt(sos, y_rect1)

    ax[0].set_title("Eingangssignal f =%5.1f Hz" %ff)
    ax[2].set_title("Ausgangssignal")

    ax[0].plot(t,y_rect1)
    ax[2].plot(t,y_rect1, color = 'tab:blue', alpha = 0.5)
    ax[2].plot(t,y_rect1_filt, color  = 'tab:red')

    ax[0].set_xlim([0,1])
    ax[2].set_xlim([0,1])
    ax[0].set_ylim([-1.1,1.1])
    ax[2].set_ylim([-1.1,1.1])

    # Bode Plot
    ax[1].semilogx(w, 20 * np.log10(abs(h)), color = 'tab:red', lw = 2)
    ax[1].axhline(y = -3, color='k', ls = '--', lw = 1)
    ax[1].axvline(x = filter_frequenz, color='tab:red', ls = '-', lw = 1)
    ax[1].axvline(x = ff, color='tab:blue', ls = '-', lw = 1)

    #ax[1].set_xticks([1e-2, 1e-1, 0.5, 1, 10], labels = [r'$10^{-2}$', r'$10^{-1}$', '0.5', '1', '10'])
    ax[1].set_title("Tiefpass: f =%5.1f Hz" %filter_frequenz)
    ax[1].grid(True, lw=0.5, zorder=0, ls = '--', which='major', axis='both')
    ax[1].grid(True, lw=0.5, zorder=0, ls = '--', which='minor', axis='both')
    ax[1].set_ylabel("Amplitude (dB)")
    ax[1].set_xlim([1e-1,100])
    ax[1].set_ylim([-25,1])

ani = FuncAnimation(fig, animate_filtered_signals, frames=range(1, 51), repeat=False)

# Display the animation
plt.tight_layout()
plt.subplots_adjust(wspace=0.3)
plt.subplots_adjust(top=0.85)
plt.close()
ani.save('LP_rechteck.mp4', writer='ffmpeg', dpi=300)
HTML(ani.to_jshtml())

Once Loop Reflect

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
import warnings
from matplotlib.animation import FuncAnimation
from IPython.display import HTML

warnings.filterwarnings('ignore')

# Grundlegende Parameter
SAMPLE_RATE = 500.0  # Hertz
DURATION = 10  # Sekunden
t = np.linspace(0, DURATION, int(SAMPLE_RATE * DURATION), endpoint=False)
u = 1.0
    
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(10,3))

def animate_filtered_signals(filter_frequenz):
    ax[0].clear()  # Clear the previous frame
    ax[1].clear()  # Clear the previous frame
    ax[2].clear()  # Clear the previous frame

    # Tiefpass-Filter konfigurieren
    order = 1
    b, a = signal.butter(order, filter_frequenz, 'low', analog=True)
    sos = signal.butter(order, filter_frequenz, 'low', fs=SAMPLE_RATE, output='sos')
    w, h = signal.freqs(b, a)

    # 0.2 Hz & 8 Hz Sinus Signal + Gefiltert
    ff = 0.2
    y_sin3 = 0.7 * np.sin(2 * np.pi * ff * t) + 0.3 * np.sin(70 * 2 * np.pi * ff * t)
    y_sin3_filt = signal.sosfilt(sos, y_sin3)

    f = 70*ff
    ax[0].set_title("Eingangssignal Rauschen f =%5.1f Hz" %f)
    ax[2].set_title("Ausgangssignal")

    ax[0].plot(t,y_sin3)
    ax[2].plot(t,y_sin3, color = 'tab:blue', alpha = 0.5)
    ax[2].plot(t,y_sin3_filt, color  = 'tab:red')

    ax[0].set_xlim([0,5])
    ax[2].set_xlim([0,5])
    ax[0].set_ylim([-1.1,1.1])
    ax[2].set_ylim([-1.1,1.1])

    # Bode Plot
    ax[1].semilogx(w, 20 * np.log10(abs(h)), color = 'tab:red', lw = 2)
    ax[1].axhline(y = -3, color='k', ls = '--', lw = 1)
    ax[1].axvline(x = filter_frequenz, color='tab:red', ls = '-', lw = 1)
    ax[1].axvline(x = ff, color='tab:blue', ls = '--', lw = 1)
    ax[1].axvline(x = f, color='tab:blue', ls = '-', lw = 1)

    #ax[1].set_xticks([1e-2, 1e-1, 0.5, 1, 10], labels = [r'$10^{-2}$', r'$10^{-1}$', '0.5', '1', '10'])
    ax[1].set_title("Tiefpass: f =%5.1f Hz" %filter_frequenz)
    ax[1].grid(True, lw=0.5, zorder=0, ls = '--', which='major', axis='both')
    ax[1].grid(True, lw=0.5, zorder=0, ls = '--', which='minor', axis='both')
    ax[1].set_ylabel("Amplitude (dB)")
    ax[1].set_xlim([1e-1,100])
    ax[1].set_ylim([-25,1])

ani = FuncAnimation(fig, animate_filtered_signals, frames=range(1, 51), repeat=False)

# Display the animation
plt.tight_layout()
plt.subplots_adjust(wspace=0.3)
plt.subplots_adjust(top=0.85)
plt.close()
ani.save('LP_noise.mp4', writer='ffmpeg', dpi=300)
HTML(ani.to_jshtml())

Once Loop Reflect

Nicht nur im Zeitraum können Sprünge oder Impulse angelegt werden. Für diese Testfunktionen können auch die Laplace, bzw. Fourier-Transformierten berechnet werden. Auch dies ist im Frequenzraum häufig einfacher, da die Testfunktionen, wie es in der Tabelle im folgenden Bild zu erkennen ist, sehr einfach sind.

Um das Verhalten unseres eben diskutierten Bandpasses auf verschiedene Eingangssignale zu untersuchen, können wir die gleichung der Übertragungsfunktion einfach nach \(U_\mathrm a\) auflösen. Das liefert uns im allgemeinen Fall eine Gleichung für das zu erwartende Ausgangssignal:

\[U_\mathrm a = G(s) \cdot U_\mathrm e(s)\]

• Wählen wir als Eingangssignal einen Dirac-Puls, \(\delta(t)\), um die Impulsantwort zu berechnen, so erhalten wir diese in dem wir für \(U_\mathrm e(s) = 1\) einsetzen. Dies ist einfach die Laplace-Transformierte eines Delta-Peaks.

  \[U_\mathrm a = G(s) = \frac{1}{s+1}\]

• Wählen wir als Eingangssignal einen Sprung, möchten also die Sprungantwort bestimmen, so setzen wir in die Gleichung \(U_\mathrm e(s) = 1/s\), die Laplace-Transformierte einer Sprungfunktion.

  \[U_\mathrm a = G(s)\cdot \frac{1}{s} = \frac{1}{s(s+1)}\]

Hierbei handelt es sich um Faltungen im Frequenzraum, deren Berechnungen im Zeitbereich sehr viel komplizierter wäre, wie wir im nächsten Kapitel sehen werden.

Aus Übertragungsfunktionen können noch weitere Eigenschaften von Messsystemen abgeleitet werden, auf die wir hier nicht näher eingehen können. Aus den Nullstellen und Polstellen kann aber abgelesen werden, ob das System stabil ist, sprungfähig ist oder eher ein integrales Verhalten aufweist.

Hintereinanderschaltung von Messsystemen

Auch das Hintereinanderschalten von Messsystemen wird ebenfalls über die Faltung berechnet. Auch hier gilt, dass das Hintereinanderschalten von Messsystemen im Frequenzraum viel einfacher zu berechnen ist als im Zeitraum. Seien \(H_1(s)\) und \(H_2(s)\) die Übertragungsfunktionen zweier Messsysteme, so berechnet sich deren Hintereinanderschaltung und damit deren Gesamt-Übertragungsfunktion:

• im Zeitraum: \(h(t) = h_1(t) \ast h_2(t)\)

• im Frequenzraum: \(H(s) = H_1(s) \cdot H_2(s)\)

• im Frequenzraum addieren sich die Amplituden (in dB!) im Bode-Diagramm: \(|H_\mathrm{dB}(s)| = |H_{1,\mathrm{dB}}(s)| + |H_{2,\mathrm{dB}}(s)|\)

Als Beispiel soll uns ein Bandpass dienen, der aus der Hintereinanderschaltung eines Hoch- und Tiefpasses realisiert werden kann. Im Folgenden Bild sind die Komponenten des Tiefpasses (TP) blau dargestellt, die des Hochpasses (HP) rot dargestellt. Der Tiefpass lässt tiefe Frequenzen bis zu seiner Grenzfrequenz passieren (bis auf die 71% Signalverlust) und der Hochpass lässt hohe Frequenzen bis zu seiner Grenzfrequenz passieren. Wir wählen C und R der beiden elektronischen Schaltungen so, dass die Grenzfrequenz der Hochpasses unterhalb der des Tiefpasses liegt, also \(f_\mathrm{HP} < f_\mathrm{TP}\). Der Amplitudengang ist rechts im folgenden Bild geplottet:

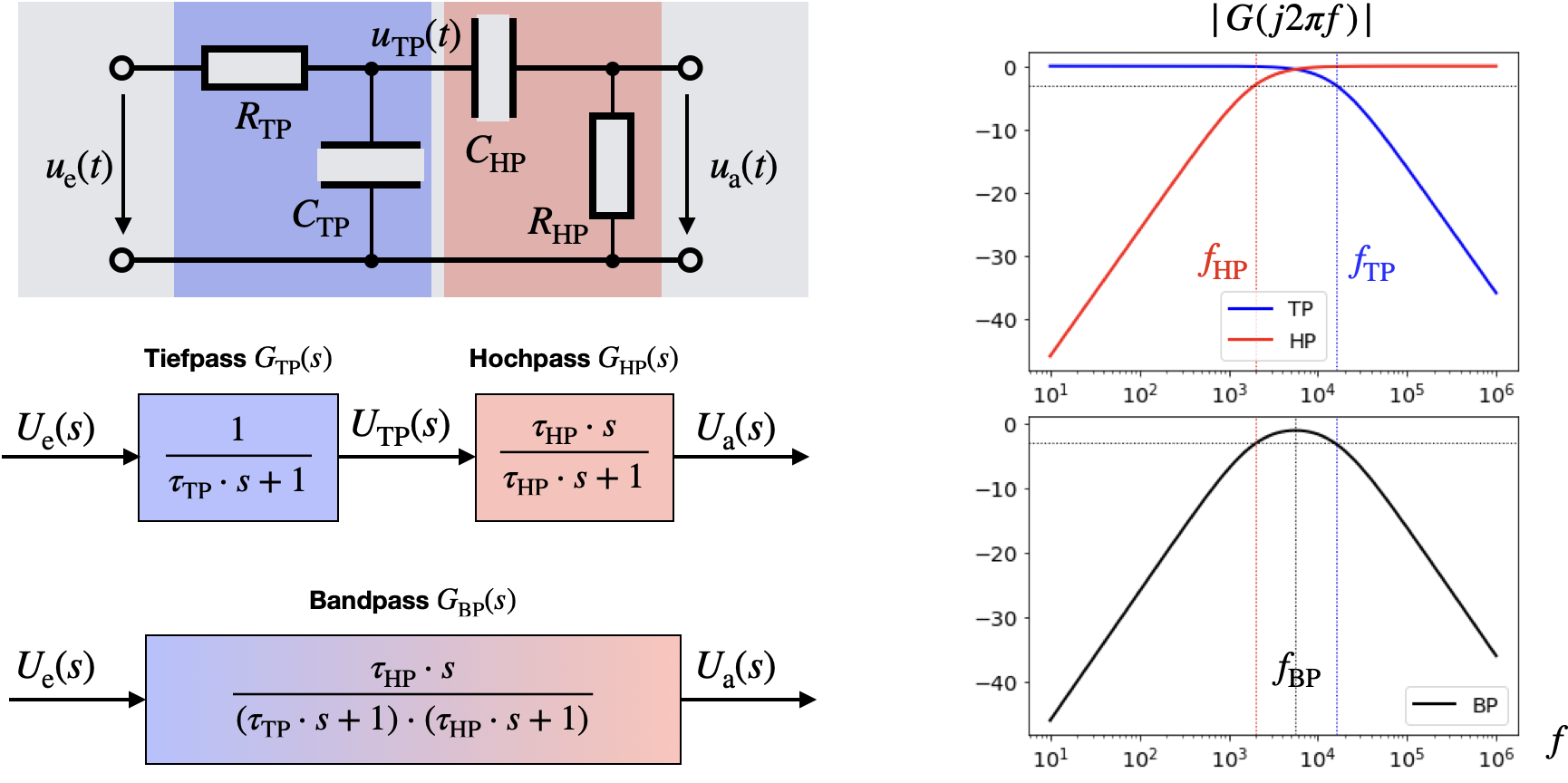
Hintereinanderschaltung im Bode Diagramm

Wird die Übertragungsfunktionen in Einheiten von dB gezeichnet, also logarithmisch aufgetragen, so ergibt sich eine weitere grafische Vereinfachung bei der Kombination: In logarithmischen Einheiten können die einzelnen Übertragungsfunktionen in einem Amplitudengangs-Plot addiert (!) statt multipliziert werden.

Referenztabelle Laplace-Transformation

\(\sigma(t)\) ist die Sprungfunktion und \(\delta(t)\) der Delta-Dirac-Puls.

Originalfunktion \(u(t)\)	Bildfunktion \(U(s)\)
\(\delta(t)\)	\(1\)
\(\sigma(t)\)	\(\frac{1}{s}\)
\(\mathrm e^{-at} h(t)\)	\(\frac{1}{s+a}\)
\(\cos(\omega_0 t)\)	\(\frac{s}{s^2 + \omega_0^2}\)
\(\sin(\omega_0 t)\)	\(\frac{\omega_0}{s^2 + \omega_0^2}\)
\((1-\mathrm e^{-at}) h(t)\)	\(\frac{a}{s(s+a)}\)
\(\mathrm e^{-at} \cos(\omega_0 t)\)	\(\frac{s+a}{(s+a)^2 + \omega_0^2}\)
\(\mathrm e^{-at} \sin(\omega_0 t)\)	\(\frac{\omega_0}{(s+a)^2 + \omega_0^2}\)
\(\delta(t)t\)	\(\frac{1}{s^2}\)